This section contains a list of all the websites that we consider belong to the network beyond reasonable doubt.
The list is also available in JSON format at: github.com/cirosantilli/media/blob/master/cia-2010-covert-communication-websites/hits.json. When there are new additions we keep the JSON up to date with the help of the following OurBigBook Markup to JSON conversion helper ../cia-2010-covert-communication-websites/bigb-to-json:and new results that have been added to the list below can automatically be merged with ../cia-2010-covert-communication-websites/bigb-to-json-merge:We have also made a dump of the websites extracted from the Wayback Machine at: github.com/cirosantilli/cia-2010-websites-dump
cia-2010-covert-communication-websites/bigb-to-json cia-2010-covert-communication-websites.bigbcia-2010-covert-communication-websites/bigb-to-json-merge > tmp.json
mv tmp.json ../media/cia-2010-covert-communication-websites/hits.jsonThe main criteria to consider a website as a hit is for it to have a Wayback Machine archive with an archived communication mechanism. JS comms are always quickly visually inspected, other mechanisms we look only at filename patterns for now. We also consider as hits websites that don't have archived comms, often the case for CGI comms, but which have two ore more of the following supporting evidence:Commented edge cases that didn't make the cut can be found mostly under Section "IP range search" and Section "2013 DNS Census virtual host cleanup heuristic keyword searches".
- shares an IP range with other website
- a Wayback Machine archive or cqcounter screenshot strongly confirming visual style
- an archived broken link to the possible comms
| ip | domain | Wayback Machine | language | country mentions | comms | theme | notes |
|---|---|---|---|---|---|---|---|
| ? | 24hoursprimenews.com | 2009 | English | JAR | news | split images[ref][ref] | |
| ? | cyhiraeth-intlnews.com | 2011 | English | JAR | news | en.wikipedia.org/wiki/Cyhyraeth "The cyhyraeth is a ghostly spirit in Welsh mythology, a disembodied moaning voice that sounds before a person's death." WTF! So the serious looking black actress lady is meant to represent the voice of death?. Split images[ref][ref]. rss-items. Here she is on Getty Images: www.istockphoto.com/photo/natural-style-for-the-individual-gm171403107-26684547 by Urilux | |
| ? | dailynewsandsports.com | 2013 | English | JAR | sports | ||
| ? | differentviewtoday.com | 2011 | English | JAR | news | split images, JAR unarchived | |
| ? | euronewsonline.net | 2010 | English | JAR | news | a.newslink. The image of the woman reading newspapers reverse searches to www.istockphoto.com/photo/news-gm101581053-7410445, iStock from Getty images. Copyright 2007. | |
| ? | europeannewsflash.com | 2011 | English | JAR | news | Split images[ref][ref] | |
| ? | farsi-newsandweather.com | 2011 | Farsi | Iran | JAR | news | split images[ref][ref] |
| ? | financecentraltoday.com | 2011 | English | JAR | news, finance | unusual td > p > strong article list. Copyright 2008. | |
| ? | firstnewssource.com | 2011 | Farsi | Iran | JAR | news | Copyright 2009. Split images. rss-items. |
| ? | global-view-news.com | 2011 | English | JAR | news | split images[ref][ref] | |
| ? | globaltourist.net | 2010 | English | JAR | travel | split images[ref][ref], rss-items. speed.jar "speed test" JAR pattern. The split headers have a weird style however <li><a id="banner1"> </a></li> and then filled with a CSS background image. This is a weird one, there is some chance that it is a legit website in the CIA style. Notably, at least as of August 2012 it had become a wordpress site marked "Just another Media Network Online Sites site", which is a bit early. Likely they just watch for good domain drops and take over quickly. The last in-style archive is from March 2012, which is first followed by a Godaddy parked domain on April 2012. This domain also has a 2003 archive which is almost certainly from the same authors as it also has a link to globaltourist.net/speed.jar and the upper left image is the same. Its history does however remember us of alljohnny.com, which had its 2004 version and then a 2010 rehash. Both of these versions contain ImageReady Slices mentions in them, characteristic of the split header images fingerprint. | |
| ? | hassannews.net | 2010 | Arabic | SWF | news | CSS or archive quite broken. Split images[ref][ref]. rss-items. cqcounter.com/whois/www/hassannews.net.html not found. The arabic title is "حسن الأخبار" (good news) and the domain seems to be a transliteration of it. | |
| ? | health-men-today.com | 2011 | Arabic | JAR | news | rss-items. Encoding broken. cqcounter.com/whois/www/health-men-today.com.html also broken. Same registrar as medicatechinfo.com: Jason Noll IP and DNS metadata. Closely related stock model image comically used as the image of the Gay Arab Central community on the. Copyright 2008. | |
| ? | inkfreenews.com | 2011 | English | JAR | news | split images, JAR unarchived | |
| ? | internationalnewsworthiness.com | 2011 | English | JAR | news | RSS, split images, JAR unarchived | |
| ? | intlnewsdaily.com | 2011 | English | JAR | news | rss-items | |
| ? | intoworldnews.com | 2011 | English | JAR | news | split images. Links to news websites from frontpage, not news themselves. | |
| ? | iranfootballsource.com | 2011 | Farsi | JS | sports, football | ||
| ? | iraniangoalkicks.com | 2008 | Farsi | Iran | JAR | sports, football | |
| ? | iraniangoals.com | 2009 | Farsi | Iran | JS | sports, football | |
| ? | latinamericanewsbeat.com | 2010 | English | JAR | news | split images. Also has an archived "register" link at the bottom: web.archive.org/web/20101114045007/http://latinamericanewsbeat.com/register.html but it reads "We are currently unable to register new members while we upgrade our site. Please check back soon." | |
| ? | magneticfieldnews.com | 2010 | English | JAR | news | rss, split images | |
| ? | middle-east-newstoday.com | 2010 | Farsi | JS | news | rss, split images | |
| ? | mideasttoday.net | 2010 | Farsi | JAR | news | a.rss-item, split images, copyright 2008 | |
| ? | mydailynewsreport.com | 2011 | Pashto | Afghanistan | JAR | news | rss, split images |
| ? | mynepalnews.com | 2011 | English | JAR | news | Split images with <li><a id="banner1"> </a></li> style. Nice swimsuit ad. The bottom bar "Copyright © 2008 My Nepal News, LLC. All Rights Reserved." is also kind of typical, see e.g. web.archive.org/web/20110208042144/http://helpinghandssite.com/, both have <!-- begin #footer --> and <div id="footer">. ingenuitytrendz.com is another closely related template. One ridiculously mind blowing thing about this website is the presence of Webalizer reports under /stats e.g.: /stats. This fact is so mind blowing that it makes us question if this an actual hit or just style coincidence. Particularly ridiculous is the presence of inurl:cgi server_software at web.archive.org/web/20110204095809/http://mynepalnews.com:80/stats/usage_200805.html which is almost certainly a Google dork search, which we know is something that the Iranians used to find the websites. Also of interest are link backs from at web.archive.org/web/20110204095815/http://mynepalnews.com:80/stats/usage_200806.html from whois.domaintools.com/mynepalnews.com and www.whois.sc/mynepalnews.com That search hits under /cgi-bin/check.cgi. That page is itself os some interest containing SERVER_ADMIN = mmadev@mmadev.com. web.archive.org/web/20110204095815/http://mynepalnews.com:80/stats/usage_200806.html also reveals several request IPs. Even if this is not a CIA website, there's a chance we could find the IP of the Iranian counter-intelligence in these IP list, it's mind blowing. And if a hit, we could also find IPs used by CIA handlers to see if the website is working. Lot's of referrer spam too as well. | |
| ? | newdaynewsonline.com | 2011 | English | JAR | news | ||
| ? | networkconnectionsite.com | 2011 | English | JS | news | rss, split images | |
| ? | news-latina.com | 2011 | English | JAR | news | copyright 2007 | |
| ? | newsdelivered.net | 2010 | English | JAR | news | rss, split images, JAR unarchived | |
| ? | newsincirculation.com | 2011 | Arabic | JAR | news | ||
| ? | newsworldsite.com | 2011 | Pashto | Afghanistan | JAR | news | |
| ? | opensourcenewstoday.com | 2010 | Arabic | JAR | news | copyright 2010 | |
| ? | outlooknewscast.com | 2011 | Farsi | Iran | JAR | news | |
| ? | pars-technews.com | 2011 | Farsi | Iran | JAR | news | "pars" presumably means "Parsi" or something of the same root |
| ? | pondernews.net | 2011 | Arabic | JAR | news | rss. Some archived pages use unusual paths such as /lldwg/qlaqft.php?fc=282910. | |
| ? | profile-news.com | 2011 | English | JAR | news | a.newslink | |
| ? | purlicue-news.com | 2011 | English | JAR | news | split images, rss | |
| ? | segomonews.com | 2011 | English | JAR | news | rss, split images. TODO meaning of "segomo"? The main Wikipedia hit is a Gallo-Roman God, but the website is focused on Asia? | |
| ? | shadesofnews.com | 2011 | Arabic | JAR | news | a.rss-item, split images. Also has a second from 2013 JAR at: web.archive.org/web/20131229092754/http://shadesofnews.com/sptgms213.jar and a raw .class crime.Business.class which replies with "The requested document was not found on this server". Copyright 2009. | |
| ? | sportsnewsfinder.com | 2011 | Chinese | China | JAR | news | 体育新闻发现者 (sports news finder) |
| ? | techwatchtoday.com | 2011 | English | JAR | tech, news | Marked copyright 2008. Split images[ref][ref]. Later legit. | |
| ? | terrain-news.com | 2011 | Pashto | Afghanistan | JAR | news | |
| ? | todayoutdoors.com | 2011 | English | JAR | sports, travel | split images[ref][ref] | |
| ? | todaysnewsreports.net | 2010 | Arabic | JAR | news | ||
| ? | weblognewsinfo.com | 2011 | English | JAR | news | Split images, rss-items. | |
| ? | wiredworldnews.com | 2011 | English | JAR | tech | split images, copyright 2008 | |
| 62.22.60.40 | travel-passage.com | 2011 | English, Chinese | travel | No Wayback Machine archives of toplevel, only of the 航空 Flight Reservations subpage: web.archive.org/web/20091118013330/http://travel-passage.com:80/service-flights.htm. The link to it can be seen from the cqcounter screenshot. The page contain an unusual mixture of Chinese and English. The Chinese title is 游行连接 (lit. travel connection) | ||
| 62.22.60.42 | newsupdatesite.com | 2011 | English | JAR | news | split images, rss-item. JAR unarchived. | |
| 62.22.60.46 | flyingtimeline.com | 2011 | English | JAR | airplanes | ||
| 62.22.60.48 | currentcommunique.com | 2011 | English | Egypt | SWF | news | |
| 62.22.60.49 | telecom-headlines.com | 2011 | English | JS | tech | ||
| 62.22.60.52 | collectedmedias.com | 2011 | French | JS | news | Marked copyright 2008 | |
| 62.22.60.54 | romulusactualites.com | 2011 | French | France | news | ||
| 62.22.60.55 | thefilmcentre.com | 2011 | English | JS | films | ||
| 62.22.60.56 | traveltimenews.com | 2011 | English | JS | news | ||
| 62.22.61.193 | awfaoi.org | 2010 | Arabic | Iraq | JAR | not-for-profit | This was the first clear .org hit with comms we've been able to find. Title translation: "Arab women to help Iraq", so perhaps "awfaoi" stands for "Arab Women For A O? Iraq". This fits well into the .org theme. Marked copyright 2008. |
| 62.22.61.197 | rc5sports.com | 2011 | English | JAR | sports | ||
| 62.22.61.198 | inside-vc.com | 2011 | English | CGI | finance | "vc" is a standard abbreviation for venture capital. Previously legit circa 2004: web.archive.org/web/20030306171752/http://www.inside-vc.com/ | |
| 62.22.61.200 | zerosandonesnews.com | 2011 | English | SWF | news | rss, split images | |
| 62.22.61.202 | bailsnboots.com | 2011 | English | SWF | sports, cricket | "Bail" is one part of the thing your're supposed to hit with th eball in cricket.[ref] | |
| 62.22.61.203 | the-cricketer-online.com | 2011 | English | JAR | sports, cricket | marked copyright 2009. | |
| 62.22.61.204 | hollywoodscreen.net | 2011 | English | JS | films | ||
| 62.22.61.206 | worldnewsnetworking.com | 2011 | Arabic | JAR | news | ||
| 62.22.61.212 | nuestrasfinanzas.com | 2011 | Spanish | JAR | finance | ||
| 62.22.61.213 | sandstormnews.com | 2011 | Arabic | SWF | news | rss, split images | |
| 62.22.61.215 | the-tech-mind.com | 2011 | English | technology, news | Welcome to the US Petabox on Wayback Machine. | ||
| 62.22.61.217 | court-masters.com | 2011 | English | JAR | sports, tennis | ||
| 62.22.61.219 | allworldstatistics.com | 2011 | English | JS | statistics | ||
| 62.22.61.220 | newsjaka.com | 2011 | English | Indonesia | JS | news | "jaka" presumably means Jakarta, the capital of Indonesia. There is a Indonesia section on the left sidebar. But the news are quite global however. Photo source: www.shutterstock.com/image-photo/little-boat-on-bratan-lake-front-5860873 depicts "Bratan lake in front of the Pura Ulu Danau temple" by Ine Beerten. Pinged her at: portfolio.inebeerten.be/#Contact |
| 63.131.229.2 | fightskillsresource.com | 2011 | English | JS | sports, martial arts | Getty Images for the karate dude: www.istockphoto.com/photo/take-off-gm98702037-1196239 | |
| 63.131.229.4 | unitedterritorynews.com | 2011 | English | JS | news | ||
| 63.131.229.9 | show-dustry.com | 2011 | English | CGI | entertainment | The website name is a neologism with "show" and "industry". | |
| 63.131.229.11 | mythriftytrip.com | 2010 | English | CGI | travel | thrifty means: "using money and other resources carefully and not wastefully" | |
| 63.131.229.12 | cyberreportagenews.com | 2011 | English | JAR | news | rdns source | |
| 63.131.229.13 | sunrise-news.com | 2011 | English | JAR | news | rdns source | |
| 63.131.229.15 | cricketnewsforindia.com | 2013 | English | India | JS | sports, cricket | archive quite broken, lots of missing files, including the JS. cqcounter.com/whois/www/cricketnewsforindia.com.html in style. |
| 63.131.229.16 | nutricion-saludable.net | 2010 | Spanish | CGI | health | Also under nutricion-saludable.info. There is weirdly a single page archived from 2008: epages/nutricion-saludable_net.sf with this weird .sf extension. It is HTML however. It says: "Lo sentimos, la tienda está actualmente cerrada por razones técnicas. Pronto estaremos a tu disposición. Si lo deseas puedes ponerte en contacto con nosotros en el tel: 651 80 76 19". This appears to be a spanish phone number: without country code, which would be +34[ref]. | |
| 63.131.229.20 | fixashion.net | 2011 | English | JS | fashion | ||
| 63.130.160.50 | theglobalheadlines.com | 2010 | English | JAR | news | this has several archives from 2013, marked as Live Web Proxy Crawls and explained "mostly by the Save Page Now", so presumably by counter intelligence or amateurs | |
| 63.130.160.51 | hai-pow.com | 2011 | English | JAR | sports, martial arts | ||
| 63.130.160.53 | echessnews.com | 2011 | Chinese | China | JAR | sports, boxing | Chinese title: 我的象棋世界 (My Chinese Chess world). rdns source. Split images[ref][ref] |
| 63.130.160.60 | boxingstop.net | 2010 | Polish | Poland | JAR | sports, boxing | |
| 63.130.160.61 | bookmarksthis.com | 2010 | English | JAR | books | A book review website. Shows a stock model reading a book and their signature black print over decorations on top | |
| 63.130.160.62 | azerinews.org | 2009 | Azerbaijani | Azerbaijan | JAR | news | rdns source. Split images, rss-items. "Azeri" is a word that denotes the people from the region of Azerbaijan. |
| 64.16.204.53 | bosniakbusinessnews.com | 2011 | English | Bosnia | business | A Bosniak is someone from an ethnicity from Bosnia | |
| 64.16.204.54 | affairesdumonde.com | 2011 | French | news | |||
| 64.16.204.55 | holein1news.com | 2010 | English | JAR | sports, golf | ||
| 64.16.204.58 | tech-topix.com | 2013 | English | CGI | tech | Archive quite broken, but link to CGI comms. Copyright 2010. cqcounter.com/whois/www/tech-topix.com.html not found. | |
| 65.61.127.161 | european-footballer.com | 2011 | Croatian | Sports, football | Broken Wayback Machine archive: web.archive.org/web/20110319111233/http://european-footballer.com/. The title was "Europski Nogometaš" (European football player). The CQ Counter screenshot clarifies that the surviving Wayback Machine archive contains only a sidebar. It is unlikely to contain comms therefore. | ||
| 65.61.127.163 | capture-nature.com | 2011 | English | JAR | photography | Reuters example. Since became legitimate, Ciro contacted the owner, and he was unaware of the domain's history. | |
| 65.61.127.166 | globalnewsbulletin.com | 2013 | English | Tunisia, Afghanistan, Iran, Egypt | CGI | news | PHP pages, images /images/index_01.jpg |
| 65.61.127.167 | internationalwhiskylounge.com | 2011 | English | CGI | news | No Wayback Machine archives. There's a "Log-in" tab so CGI comms likely. Stock image used of young woman with a glass of Whisky: www.istockphoto.com/photo/the-girl-with-glass-of-whisky-gm94997193-11328059 by alarich | |
| 65.61.127.168 | the-golden-rule.info | 2011 | English | finance, news | Website error archived at: web.archive.org/web/20131011012026/http://the-golden-rule.info/ | ||
| 65.61.127.169 | crossovernews.net | 2011 | English | JAR | sports, basketball | ||
| 65.61.127.170 | newsidori.com | 2011 | English | news | Very broken 2013 archive: web.archive.org/web/20130714134510/http://www.newsidori.com/. "Idori" sounds Japanese, but the meaning is unclear even after the cqcounter screenshot! It's just random US news, nothing to do with Japan. | ||
| 65.61.127.171 | nrgconsultingandnews.com | 2011 | English | news | It is in English but contains several mentions of Brazil. Entitled: "Energy Consulting News Forum" | ||
| 65.61.127.171 | premierstriker.com | 2011 | English | sports, football | No Wayback Machine archives from the time, and has been since parked by something apparently as of 2022 onwards. Entiled "Premier striker" | ||
| 65.61.127.174 | dedrickonline.com | 2010 | German | JS | sports | ||
| 65.61.127.175 | altworldnews.com | 2013 | English | CGI | news | Epoch times link, PHP pages | |
| 65.61.127.176 | american-historyonline.com | 2011 | English | history | No Wayback Machine archives | ||
| 65.61.127.177 | material-science.org | 2009 | English | science, material science | No comms found, and slightly innovative design. Comms could be CGI under web.archive.org/web/20091213032538/http://material-science.org/services.htm or web.archive.org/web/20091213032538/http://material-science.org/equipment.htm. But marking it as hit because .rss-item + IP range. | ||
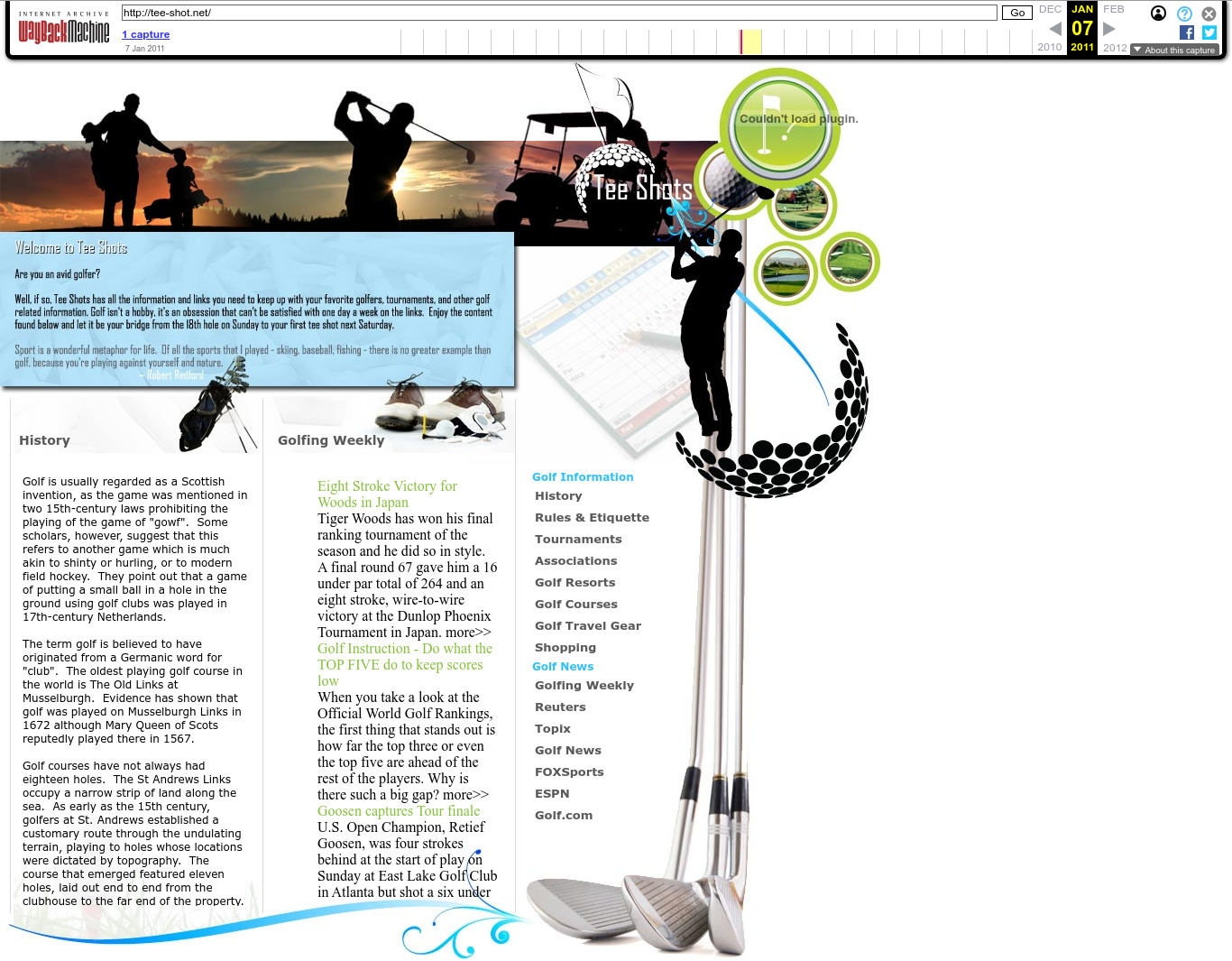
| 65.61.127.178 | tee-shot.net | 2011 | English | SWF | sports, golf | nice domain name | |
| 65.61.127.180 | screencentral.inf | 2011 | English | Afghanistan | cinema | Rather innovative design, but hit likely. Welcome to US Petabox: web.archive.org/web/20130713224951/http://screencentral.info/. | |
| 65.61.127.181 | worldnewsandtravel.com | 2011 | English | news | No Wayback Machine archives | ||
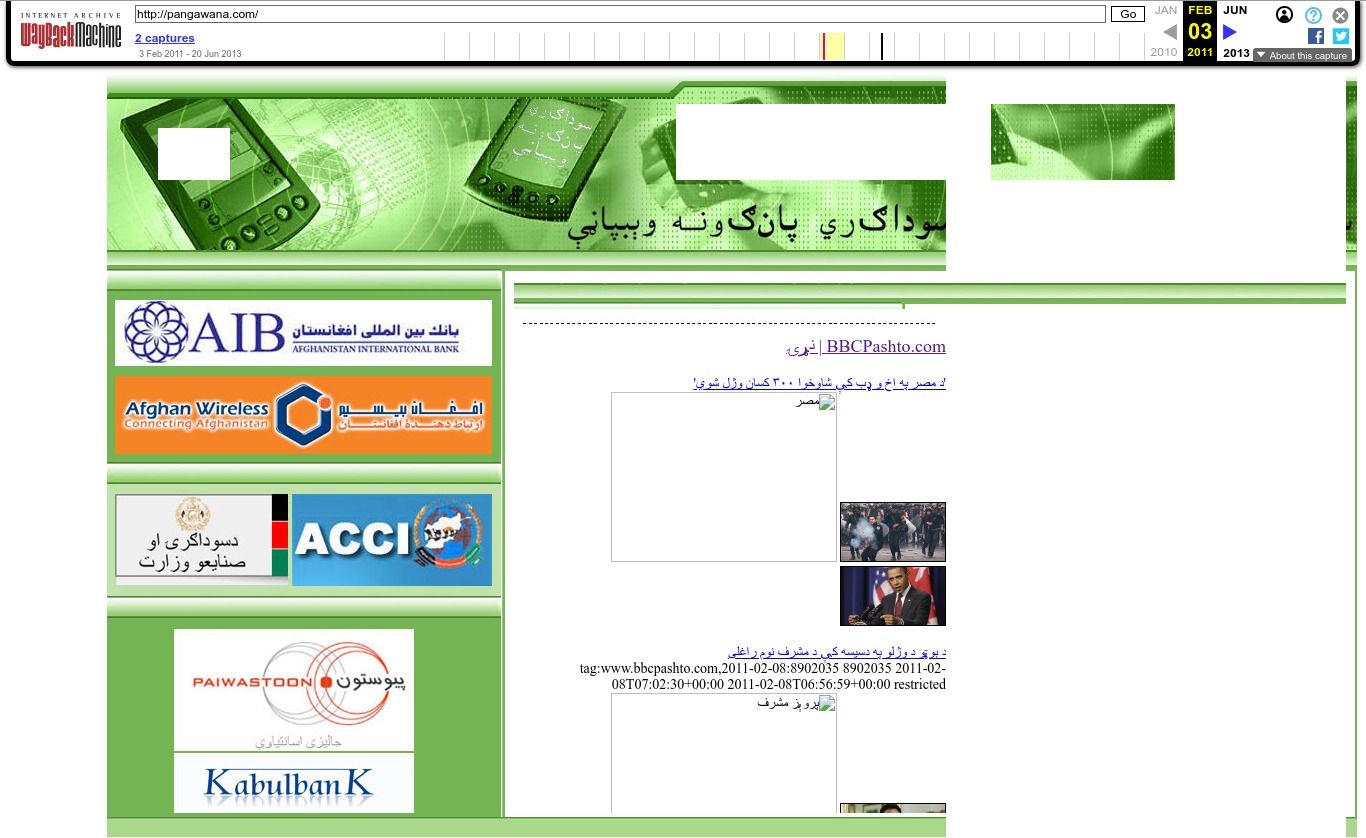
| 65.61.127.182 | pangawana.com | 2011 | Arabic | Afghanistan | JS | news | |
| 65.61.127.183 | cutabovenews.com | 2011 | English | Algeria, various others | JS | sports, basketball | The globe on Shutterstock: www.shutterstock.com/image-illustration/creative-drawing-charts-graphs-business-success-211092952 by rzoze19. Pinged him at: x.com/cirosantilli/status/1899748328549609700 |
| 65.61.127.184 | worldwildlifeadventure.com | 2011 | English | JAR | travel | ||
| 65.61.127.186 | explorealtmeds.com | 2013 | English | JAR | health | the JAR was not archived, but there's a link to it | |
| 65.218.91.9 | rolling-in-rapids.com | 2010 | English | sports, kayak | Found by searching for "Glaze, L.", registrar of alljohnny.com, on tools.whoisxmlapi.com/reverse-whois-search | ||
| 65.218.91.9 | welcometonyc.net | 2010 | English | CGI | travel | ||
| 65.218.91.17 | alljohnny.com | 2004 | English | CGI | fansite | mega early hit from 2004 to 2005. Then a gap, then they redid the domain: 2011. Same authors given content similarities e.g. "Submit Your Favorite Carson Moment". Reusing the domain after all these years, the lack of OPSEC is just mind blowing! New website marked Copyright 2003. Part of Oleg Shakirov's findings. One of the Reuters websites. Search documented at: Searching for Carson. Carson is also featured, although less proeminently, at webofcheer.com. There must have been some massive Johnny Carson fan among the contractors a that time! | |
| 66.45.179.192 | thegraceofislam.com | 2011 | English | CGI | religion, Islam | ||
| 66.45.179.193 | arabicnewsunfiltered.com | 2011 | Arabic | JAR | news | rdns source | |
| 66.45.179.194 | raulsonsglobalnews.com | 2011 | English | JAR | news | ||
| 66.45.179.195 | aryannews.net | 2010 | Pashto | Afghanistan | JAR | news | rdns source. Heil. |
| 66.45.179.199 | attivitaestremi.com | 2011 | Italian | CGI | sports | ||
| 66.45.179.200 | foodwineandsuch.com | 2011 | English | food | No Wayback Machine archives. Entitled "Food, wine & such". | ||
| 66.45.179.201 | hitthepavementnow.com | 2011 | English | CGI | sports, running | ||
| 66.45.179.202 | newimages.org | 2011 | Turkish | Turkey | JAR | photography | JAR unarchived |
| 66.45.179.203 | noticiascontinental.com | 2011 | Spanish | South America | CGI | news | |
| 66.45.179.205 | noticiasporjanua.com | 2011 | Spanish | JAR | news | ||
| 66.45.179.206 | podisticamondiale.com | 2010 | Italian | Italy | JAR | sports, running | marked copyright 2010 |
| 66.45.179.207 | reflectordenoticias.com | 2011 | Spanish | JAR | news | ||
| 66.45.179.208 | havenofgamerz.com | 2011 | English | CGI | gaming | marked copyright 2009 | |
| 66.45.179.209 | vejaaeuropa.com | 2011 | Brazilian Portuguese | Brazil | travel | web.archive.org/web/20130810131440/http://www.vejaaeuropa.com/: Welcome to the US Petabox. cqcounter.com/whois/www/vejaaeuropa.com.html confirms Brazilian Portuguese. Entitled "Veja a Europa" (Visit Europe, lit. See Europe) | |
| 66.45.179.210 | sa-michigan.com | 2011 | English | JAR | sports | "sa" is an abbreviation for the site title "Sports Alive" | |
| 66.45.179.211 | absolutebearing.net | 2010 | English | CGI | travel, sports, boats | ||
| 66.45.179.213 | myportaltonews.com | 2011 | English | JS | news | ||
| 66.45.179.214 | investmentintellect.com | 2011 | English | JAR | finance | ||
| 66.45.179.215 | nigeriastar.net | 2011 | English | Nigeria | JAR | news | Contains link to unarchived JAR |
| 66.104.169.163 | doctorsoncallsite.com | 2011 | English | JAR | health | ||
| 66.104.169.164 | lightandshadowonline.com | 2010 | English | JAR | photography | ||
| 66.104.169.168 | plugged-into-news.net | 2010 | English | JAR | news | JAR uses .zip extension! First instance, wow | |
| 66.104.169.169 | worldsportsite.com | 2011 | Arabic | sports | Comms not found. rss-items, split images. Has some apparently unrelated archives from 2008: web.archive.org/web/20080617213238/http://www.worldsportsite.com:80/ | ||
| 66.104.169.171 | golf-on-holiday.com | 2011 | English | JAR | sports, golf | ||
| 66.104.169.172 | perspectiva-noticias.com | 2011 | Spanish | JS | news | ||
| 66.104.169.175 | aquaswimming.com | 2009 | English | JAR | sports, swimming | ||
| 66.104.169.177 | dojo-temple.com | 2011 | English | CGI | sports, martial arts | TODO meaning of "kama"? Kama lol? | |
| 66.104.169.179 | neighbour-news.com | 2010 | English | Germany | JAR | news | Mentions of Goethe-Institut and Germany all over. JAR unarchived |
| 66.104.169.180 | medicatechinfo.com | 2010 | English | JS | health | ||
| 66.104.169.181 | brickmanfinancialnews.com | 2011 | English | JS | finance | ||
| 66.104.169.182 | casanewsnow.com | 2011 | English | JAR | JAR unarchived. TODO why "casa"? Doesn't seem to have any link to Spanish or Portuguese. | ||
| 66.104.169.184 | bcenews.com | 2011 | Albanian | Albania | JAR | news | Used to be a legit Korean website circa 2004: web.archive.org/web/20030401214602/http://www.bcenews.com/ |
| 66.104.173.163 | runakonews.com | 2011 | English | Africa | CGI | news | "Runako" is an African given name. |
| 66.104.173.164 | shoppingadventure.net | 2010 | English | JAR | travel, shopping | JAR unarchived | |
| 66.104.173.165 | entertaining-ly.com | 2011 | English | JAR | entertainment | ||
| 66.104.173.166 | zubeenews.com | 2011 | English | JS | news | "Zubee" is a Muslim name: muslimnames.com/zubee. | |
| 66.104.173.169 | smart-financeology.com | 2011 | English | JAR | finance | ||
| 66.104.173.173 | worldfeedstoday.com | 2011 | English | news | No main page Wayback Machine archives. Subpage archive: 2011 has a.newslink. Slightly innovative style with multi-language tabs. There is some potential for error, but let's consider it. world-newsfeeds.com also known on same IP but with no known archives. | ||
| 66.104.173.175 | media-coverage-now.com | 2010 | English | SWF | news | ||
| 66.104.173.176 | jbc-online-news.com | 2011 | English | JS | news | TODO meaning of "JCB". JS unarchived. | |
| 66.104.173.177 | webscooper.com | 2011 | English | JAR | news | ||
| 66.104.173.178 | dk-dcinvestment.com | 2010 | English | JAR | finance | TODO meaning of "dk;dc". | |
| 66.104.173.179 | newsforthetech.com | 2011 | English | news, tech | Welcome to the US Petabox. | ||
| 66.104.173.180 | stara-turistick.com | 2011 | Croatian | JAR | tourism | ||
| 66.104.173.181 | playbackpolitics.com | 2011 | English | JS | news | ||
| 66.104.173.182 | snapnewsfront.net | 2011 | English | Japan | JS | news | |
| 66.104.173.183 | ingenuitytrendz.com | 2011 | English | JAR | tech | ||
| 66.104.173.184 | armashoy.com | 2011 | Spanish | Spain | SWF | guns | meaning: "Weapons Today". In First World countries the CIA felt it would be safe to touch edgier subjects like guns |
| 66.104.173.185 | baocontact.com | English | JAR | HTML archive almost empty, but JAR was archived. One wonders what "bao" refers to, could be Chinese, but the small snippet of visible website is in English. | |||
| 66.104.173.186 | myworldlymusic.com | 2011 | English | Pakistan | JAR | music | JAR unarchived |
| 66.104.173.189 | hitpoint-gaming.com | 2011 | English | JS | gaming | Marked copyright 2010 | |
| 66.104.175.34 | itwebtoday.com | 2011 | English | JS | tech | ||
| 66.104.175.35 | drglobalnews.com | 2011 | English | JAR | news | TODO meaning of "dr"? rdns source. | |
| 66.104.175.36 | adilnews.net | 2010 | Arabic | SWF | news | Adil is an Arabic masculine name | |
| 66.104.175.40 | beyondnetworknews.com | 2011 | English | Egypt | CGI | news | |
| 66.104.175.41 | grubbersworldrugbynews.com | 2011 | English | JS | sports, rugby | ||
| 66.104.175.42 | news-and-sports.com | 2011 | English | JAR | news | rss, split images | |
| 66.104.175.44 | yourtripfinder.net | 2010 | English | travel | comms not found, CGI from unarchived subpage assumed | ||
| 66.104.175.45 | rollinsnetwork.com | 2011 | English | CGI | tech | Archive quite broken. CGI linked to but not archived. Seems to have been legit circa 2006. cqcounter.com/whois/www/rollinsnetwork.com.html empty from 2025. | |
| 66.104.175.46 | infosharenews.com | 2011 | English | JAR | news | ||
| 66.104.175.47 | southasiaheadlines.com | 2011 | English | Bangladesh, Bhutan, India, Maldives, Nepal, Pakistan, Sri Lanka Tibet | JAR | travel | JAR linked to but missing from archive |
| 66.104.175.48 | worlddispatch.net | 2010 | Arabic | SWF | news | ||
| 66.104.175.49 | webworldsports.com | 2011 | Arabic | JAR | sports | ||
| 66.104.175.50 | fly-bybirdies.com | 2011 | English | JAR | travel | ||
| 66.104.175.51 | businessexchangetoday.com | 2011 | English | CGI | news, finance | PHP pages | |
| 66.104.175.52 | mensajeradenoticias.com | 2011 | Spanish | CGI | news | CGI unarchived | |
| 66.104.175.53 | info-ology.net | 2010 | English | JAR | news | ||
| 66.104.175.54 | marketflows.net | 2011 | English | JAR | finance | ||
| 66.104.175.57 | metanewsdaily.com | 2010 | English | CGI | news | ||
| 66.175.106.134 | paddlescoop.com | 2011 | English | Bangladesh, Pakistan, India, England | JAR | sports, cricket | |
| 66.175.106.137 | kessingerssportsnews.com | 2010 | English | JS | sports | ||
| 66.175.106.138 | factorforcenews.com | 2009 | English | JAR | news | ||
| 66.175.106.142 | kanata-news.com | 2010 | English | Canada | JS | news | "Kanata" is a place in Ottawa, Canada. The name is likely of Indigenous origin. |
| 66.175.106.143 | thecricketfan.com | 2011 | English | JAR | news | ||
| 66.175.106.146 | inews-today.com | 2011 | English | Egypt | JAR | news | Marked copyright 2008 |
| 66.175.106.147 | starwarsweb.net | 2010 | English | SWF | fansite | well, not even the CIA can escape Star Wars. TODO identify boy. | |
| 66.175.106.148 | activegaminginfo.com | 2011 | Chinese | JAR | gaming | the website is entitled "活跃游戏" which means "Lively games", or "active games" as in the domain name itself. The center character seems to be from one of the infinitely many Romance of the Three Kingdoms games that must exist: www.gamersky.com/news/200711/82611.shtml | |
| 66.175.106.149 | feedsdemexicoyelmundo.com | 2011 | Spanish | Mexico | JS | news | |
| 66.175.106.150 | noticiasmusica.net | 2010 | Brazilian Portuguese | Brazil | JAR | music | |
| 66.175.106.155 | atomworldnews.com | 2011 | English | Egypt | JAR | news | |
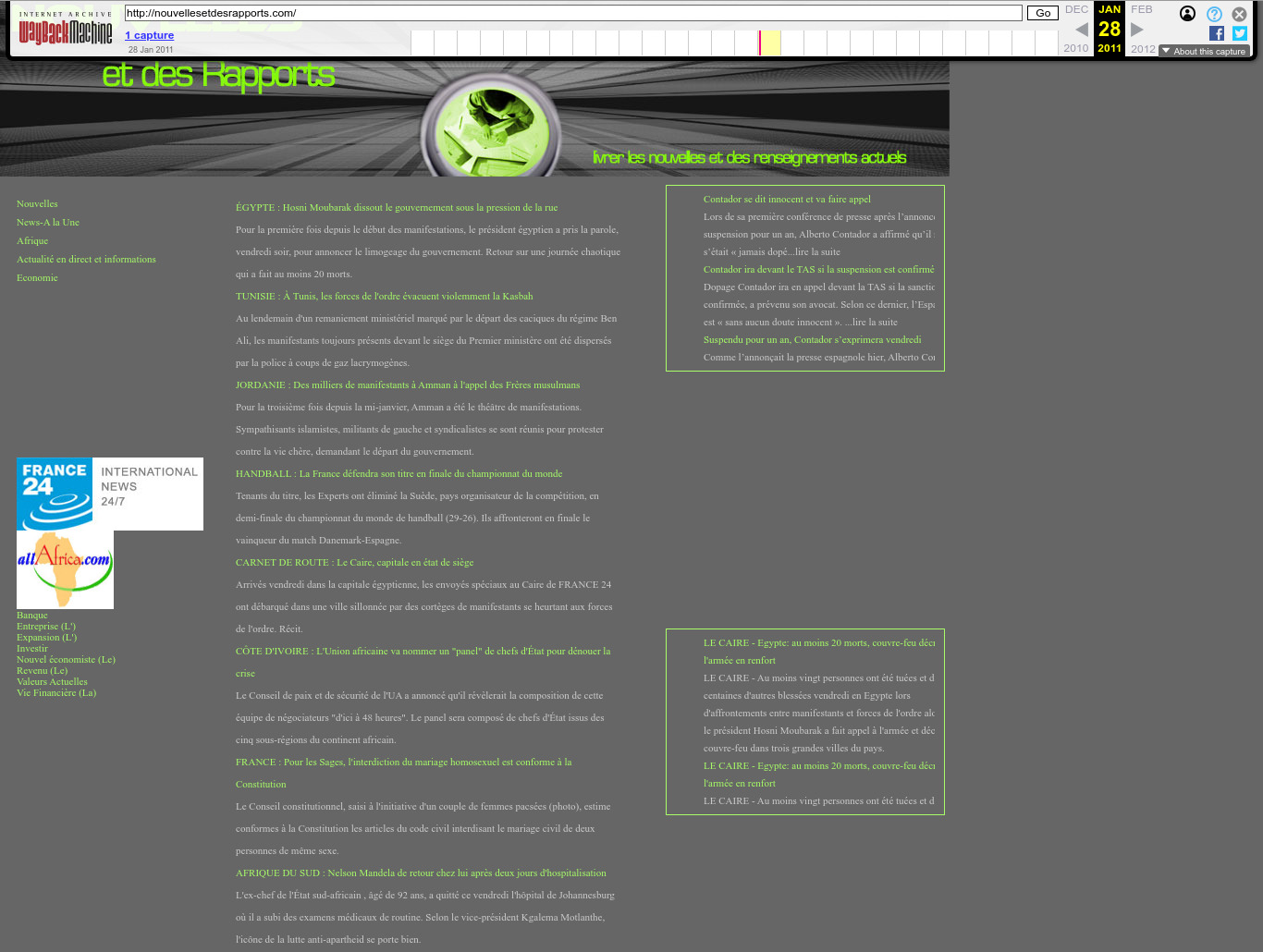
| 66.175.106.158 | nouvellesetdesrapports.com | 2011 | French | Egypt, Tunisia | JAR | news | |
| 66.237.236.227 | newsandmusicminute.com | 2011 | Pashto | JS | music | ||
| 66.237.236.229 | pearls-playlist.com | 2011 | English | SWF | music | ||
| 66.237.236.230 | beyondthefringe.info | 2012 | English | JAR | rugs | JAR unarchived | |
| 66.237.236.231 | primetimemovies.net | 2009 | English | JS | films | JS unarchived | |
| 66.237.236.235 | persephneintl.com | 2013 | JAR | archive very broken, JAR unarchived. Full title: "Persephne International", reference to Greek Goddess of "spring, the dead, the underworld, grain, and nature". cqcounter.com/whois/www/persephneintl.com.html shows us how it would have looked like. | |||
| 66.237.236.236 | directoalgrano.net | 2010 | Spanish | JAR | news | ||
| 66.237.236.240 | actualizaciondebeisbol.com | 2011 | Spanish | JS | sports, baseball | ||
| 66.237.236.243 | mygadgettech.com | 2009 | Chinese | CGI | tech | Archive very broken. cqcounter.com/whois/www/mygadgettech.com.html shows it better. The Chinese title was "我的灵巧技术". | |
| 66.237.236.247 | comunidaddenoticias.com | 2011 | Spanish | Ecuador | JAR | news | |
| 66.237.236.249 | sumerjaseahora.com | 2011 | Spanish | CGI | sports, SCUBA diving | submerge yourself now | |
| 69.84.156.69 | al-ashak-news-me.com | 2011 | Arabic | JS | news | ||
| 69.84.156.70 | theventurenews.info | 2011 | English | news | |||
| 69.84.156.71 | worldfinancetoday.net | 2011 | English | JAR | finance | ||
| 69.84.156.72 | autonewsarabia.com | 2011 | Arabic | JAR | cars | ||
| 69.84.156.74 | blue-moon-news.com | 2011 | Arabic | JS | news | ||
| 69.84.156.76 | tnc-urdu.com | 2011 | Urdu | JAR | tech | TODO meaning of "tnc"? | |
| 69.84.156.80 | noticiasdenuestromundo.com | 2011 | Spanish | news | South America focus | ||
| 69.84.156.82 | arabicnewsonline.com | 2011 | Arabic | JAR | news | rdns source. Some very similar domains: modernarabicnews.com, arabicnewsource.com. Needed more creativity here! Later legit. | |
| 69.84.156.83 | unganadormundial.com | 2010 | Spanish | CGI | sports, fitness | ||
| 69.84.156.84 | focusonbokeh.com | 2011 | English | photography | No Wayback Machine archives or broken. The design is a bit innovative, but fuck it I'll mark it as a hit. Only a "Sony" logo remains: web.archive.org/web/20110207222330/http://focusonbokeh.com/images/logo_014.jpg A photography website "Focus on Bokeh" as suggested by the domain name. reimaginepeacefulparenting.com/make-kids-happy/ contains the cute stock Asian girl. "Login" link visible suggesting CGI comms. | ||
| 69.84.156.85 | classic-rocktopia.com | 2011 | English | music, rock | Stock image e.g. at: www.dissection.nu/frames.htm | ||
| 69.84.156.87 | i7diver.com | 2011 | English | diving | |||
| 69.84.156.88 | diariodeelmundo.com | 2011 | Spanish | JAR | news | ||
| 69.84.156.89 | todaysarabnews.com | 2011 | Arabic | JAR | news | JAR unarchived. | |
| 69.84.156.90 | stickshiftnews.com | 2011 | English | JAR | cars | ||
| 69.84.156.91 | theinternationalgoal.com | 2011 | Spanish | CGI | news | ||
| 72.34.53.174 | electronictechreviews.com | 2011 | English | JAR | tech | JAR unarchived. Split images, rss-items. Present at "Mass Deface III" pastebin. | |
| 72.34.53.174 | just-the-news.com | 2011 | Arabic | JAR | news | copyright 2009. Present at "Mass Deface III" pastebin. JAR unarchived. | |
| 72.34.53.174 | kickitnews.com | 2010 | Arabic | JAR | sports, football | copyright 2009. Present at "Mass Deface III" pastebin. | |
| 72.34.53.174 | moyistochnikonlaynovykhigr.com | 2011 | Russian | Russia | fansite | copy of myonlinegamesource.com, but on a Russian transliterated domain rather than the English one, very interesting | |
| 72.34.53.174 | myhealthlibrary.net | 2011 | English | JAR | health | present at: "Mass Deface III" pastebin. | |
| 72.34.53.174 | myonlinegamesource.com | 2011 | Russian | Russia | gaming | Can't find comms, but stylistically perfect. rss-items. Present at "Mass Deface III" pastebin. | |
| 72.34.53.174 | mytravelopian.com | 2011 | English | JAR | travel | ||
| 72.34.53.174 | recursosdenoticias.com | 2011 | Spanish | JAR | news | Split images, rss-items. Present at "Mass Deface III" pastebin. | |
| 72.34.53.174 | sayaara-auto.com | 2010 | Arabic | JAR | cars | ||
| 72.34.53.174 | technologytodayandtomorrow.com | 2011 | English | JAR | tech | rss-items. Present at "Mass Deface III" pastebin. | |
| 72.34.53.174 | todaysnewsandweather-ru.com | 2011 | Russian | Russia | JS | news | JavaScript with SHAs |
| 74.116.72.227 | dayenews.com | 2011 | English | JAR | news | rdns source. Previously 69.74.45.67. | |
| 74.116.72.229 | guide-daventure.com | 2011 | French | France | JAR | travel | |
| 74.116.72.231 | bleachersfootballnews.com | 2011 | English | JAR | sports, football | TODO meaning of "Bleacher"? Possible reference to Bleacher Report. | |
| 74.116.72.232 | indirectfreekick.com | 2011 | English | JAR | sports, football | ||
| 74.116.72.233 | wwiichronicles.net | 2011 | English | CGI | history | ||
| 74.116.72.234 | petroleumagenews.com | 2011 | English | JAR | oil | ||
| 74.116.72.235 | the-open-book-online.com | 2011 | English | JS | literature | ||
| 74.116.72.236 | techtopnews.com | 2011 | English | JAR | tech | ||
| 74.116.72.238 | pohandakhbar.com | 2011 | Arabic | news | Arabic titlel: "خبرونه پوهاند" translates as "News Professor", and the domain name seems to be a transliteration of that. | ||
| 74.116.72.239 | crickettoday.info | 2013 | Pashto | JS | sports, cricket | JS unarchived. The requested URL /cricket.js was not found on this server | |
| 74.116.72.240 | zafernews.com | 2011 | Arabic | JAR | news | ||
| 74.116.72.241 | itechnewstoday.com | 2011 | English | news | "IT Tech News Today". Broken/GoDaddy takeover. | ||
| 74.116.72.242 | gdgtsource.com | 2011 | English | CGI | tech | Presumably "gdgt" stands for "GaDGeT", which is mentioned on subtitle | |
| 74.116.72.243 | waronfilmonline.com | 2011 | English | cinema | |||
| 74.116.72.244 | arborstribune.org | 2011 | news | TODO what is "Arbors"? | |||
| 74.116.72.246 | vuvuzelanews.com | 2011 | English | JAR | sports, football | Vuvuzela is this plastic horn, popular in football stadiums. The term is of African origin. Later legit. rdns source. Previously at 69.74.45.86. | |
| 74.116.72.247 | ballbatstumpsandbails.com | 2011 | English | JAR | sports, cricket | ||
| 74.116.72.248 | kioni-sailing.com | 2011 | sports, sailing | ||||
| 74.116.72.249 | round-trip-travel.com | 2010 | English | CGI | travel | this got archived a lot of times, though all seem to be Alexa crawls. | |
| 74.116.72.250 | arabicnewsource.com | 2011 | Arabic | CGI | news | ||
| 74.254.12.163 | half-court.net | 2010 | English | Philippines | JAR | sports, basketball | |
| 74.254.12.164 | dailywellnessnews.com | 2011 | English | JAR | health | rdns source. split images[ref][ref]. | |
| 74.254.12.165 | dylandon.net | 2011 | Chinese | SWF | music | "Dylan" presumably a reference to Bob Dylan? "Don" unclear. Maybe Don McLean? But it is all a bit weird given that the actual contents of the website don't seem to have anything to do with music, it appears to just be a news aggregator. | |
| 74.254.12.166 | afghanpoetry.net | 2010 | English | Afghanistan | SWF | poetry | Also at 63.131.229.10[ref] in a range. |
| 74.254.12.168 | non-stop-news.net | 2010 | Farsi | JAR | news | ||
| 74.254.12.169 | soldiersofsouthasia.com | 2011 | English | JAR | history | ||
| 74.254.12.170 | greek-news.info | 2011 | English | Greece | news | Welcome to the US Petabox. | |
| 74.254.12.171 | autism-news.org | 2011 | English | SWF | health | copyright 2007. Split images. rss-items. Previously at 69.74.45.67. | |
| 74.254.12.173 | thefreshnews.com | 2009 | English | SWF | news | rss, split images | |
| 74.254.12.176 | pakcricketgrd.com | 2011 | Urdu | JAR | sports, cricket | TODO meaning of "grd" | |
| 74.254.12.177 | networkofnews.com | 2011 | English | JAR | news | rdns source. Later legit. | |
| 74.254.12.179 | wineconnaisseur.net | 2010 | English | JS | wine | ||
| 74.254.12.187 | efiinvestment.com | 2011 | English | finance, news | TODO meaning of EFI | ||
| 74.254.12.180 | helpinghandssite.com | 2011 | English | JAR | news | ||
| 74.254.12.188 | first-tee-golf.com | 2011 | English | JAR | sports, golf | ||
| 74.254.12.189 | fabu-foto.com | 2011 | English | CGI | photography | ||
| 74.254.12.190 | viptravelabroad.com | 2011 | English | JS | travel | ||
| 174.133.70.18 | dryterrainnews.com | 2011 | English | Africa | JAR | news | rss |
| 174.133.70.18 | thefootball-life.com | 2011 | English | JS | sports, football | rss, split images | |
| 174.133.70.18 | thenewsofpakistan.com | 2009 | English | Pakistan | JAR | news | a.rss-item, split images |
| 174.133.70.18 | totallynewsnow.com | 2011 | English | JS | news | rss | |
| 199.19.110.7 | classymotors.net | 2011 | English | JS | cars | rss-items | |
| 199.19.110.7 | russiansportsworld.com | 2010 | English | JS | sports | Split headers. Unarchived middle frame, visible at: dawhois.com/www/russiansportsworld.com.html. Russian title: "Русский мир спорта" (Russian world of sport) | |
| 199.19.110.7 | theworldnewsfeeds.com | 2011 | English | JAR | news | rss-items. Split images[ref][ref] | |
| 199.19.110.7 | urbestbod.com | 2011 | Chinese | CGI | sports, fitness | No Wayback Machine archives. Broken Chinese site as usual for their archives. The headline: "你最好的身体.最好的健康和健身信息" translates as "Your Best Body The best health and fitness information", so we understand that the domain name is a super broken "your best body". Visible is a link to "论坛" (forum), so likely CGI | |
| 199.85.212.105 | mide-news.com | 2010 | English | CGI | news | "MIDE" stands for "Middle East". Comms not archived, presumably CGI comms variant. | |
| 199.85.212.111 | newsandsportscentral.com | 2009 | English | JAR | news | rdns source | |
| 199.85.212.118 | just-kidding-news.com | 2011 | English | JAR | news | epic name | |
| 199.187.208.12 | webofcheer.com | 2011 | English | JAR | fansite, comedy | has a an unarchived "members only!" section pointing to webofcheer.com/member.html, CGI comms variant. Copyright 2005! Features Johnny Carson, Charles Chaplin, Rowan Atkins, The Three Stooges and some other Americans no one knows about anymore. There must have been a massive Johnny Carson amongst the CIA contractors at that time given alljohnny.com! The HTML page is weirdly titled pg1c. Interesting, feels like a leak of the site generation system. | |
| 199.187.208.12 | world-news-online.net | 2010 | English | JAR | news | a.rss-item, split images | |
| 204.176.38.130 | i-pressnews.com | 2011 | English | JAR | news | ||
| 204.176.38.132 | turkishnewslinks.com | 2011 | English | Turkey | JAR | news | |
| 204.176.38.133 | globalcitizennews.net | 2010 | English | JAR | news | rss, split images | |
| 204.176.38.134 | photographyarecord.com | 2011 | English | CGI | photography | Cute | |
| 204.176.38.135 | breakingthewicket.com | 2011 | English | CGI | sports, cricket | ||
| 204.176.38.136 | politicalworldtoday.com | 2011 | English | Egypt | JAR | news | |
| 204.176.38.137 | hi-tech-today.com | 2011 | English | JAR | tech | ||
| 204.176.38.139 | bigscreenbattles.com | 2011 | English | JAR | films | ||
| 204.176.38.141 | rakotafootball.com | 2011 | English | JAR | sports, football | "Rakota" is an Indian family name | |
| 204.176.38.143 | noticiassofisticadas.com | 2011 | Spanish | CGI | news | ||
| 204.176.38.142 | senderosdemontana.com | 2011 | Spanish | JS | sports, cycling | Talks about mountain biking and Eurobike 2010, so likely Spain focused, but it is not direct enough to be certain. JS unarchived. | |
| 204.176.38.144 | techno-today.com | 2011 | English | JAR | tech | was legit previously. | |
| 204.176.38.145 | tickettonews.com | 2011 | English | JAR | news | rdns source. Epoch times link. | |
| 204.176.38.146 | dps-digitalphotosharing.com | 2011 | English | JAR | photography | ||
| 204.176.38.147 | theputtingreen.com | 2011 | English | JAR | sports, golf | ||
| 204.176.38.149 | sportsnewstodayar.com | 2011 | Arabic | Lebanon, others | JAR | sports | "ar" on domain name presumably means "Arabic" |
| 204.176.38.159 | kairuafricanews.com | 2011 | English | Africa | JAR | news | what is "Kairu"? en.wikipedia.org/wiki/Kairu a place in India? en.wiktionary.org/wiki/kairu "frog" in Japanese? rdns source |
| 204.176.39.97 | beamingnews.com | 2011 | Arabic | JAR | news | Nice design. rdns source | |
| 204.176.39.98 | cubriendonoticias.com | 2011 | Spanish | JAR | news | archive quite broken. JAR unarchived. cqcounter.com/whois/www/cubriendonoticias.com.html not found. | |
| 204.176.39.100 | rowleyworldpost.com | 2011 | English | Egypt, others | JAR | news | |
| 204.176.39.103 | economicnewsbuzz.com | 2011 | Korean | CGI | finance | Love the kawaii style | |
| 204.176.39.104 | spectranewsonline.com | 2011 | English | CGI | news | marked copyright 2010. | |
| 204.176.39.105 | entertainmentnewscompany.com | 2011 | Chinese | SWF | films, music | Title: "娱乐新闻公司", lit. Entertainment News Company | |
| 204.176.39.110 | arabnewsatdawn.com | 2011 | Arabic | CGI | news | cute, the Arab chick's ice cream actually has a cocktail umbrella on it. Marked copyright 2010. Here she is: www.shutterstock.com/image-photo/young-veiled-woman-reading-newspaper-eating-4836766 by Anneka. Pinged her privately on www.facebook.com/Anyka.Fotografie. | |
| 204.176.39.115 | globalprovincesnews.com | 2010 | Arabic | JS | news | The largest HTML by far so far at 328 KiB | |
| 204.176.39.116 | mahparah-news.com | 2011 | Farsi | JS | news | ||
| 204.176.39.119 | commercialspacedesign.com | 2013 | Farsi | CGI | architecture | C O N C E P T U A L design. A rare example of a fake company website. | |
| 207.150.191.68 | kickofffootballnews.com | 2010 | English | CGI | sports, football | rss-item. archive quite broken, comms not found. "login" link web.archive.org/web/20100512232600/http://kickofffootballnews.com/login.html to unarchived, so CGI comms likely. cqcounter.com/whois/www/kickofffootballnews.com.html in-style. | |
| 207.150.191.68 | mywebofnews.com | 2011 | Arabic | JAR | news | Split images[ref][ref]. rss-items. | |
| 207.150.191.68 | technologypresstoday.com | 2011 | Farsi | JAR | news | split images, RSS | |
| 207.150.191.68 | worldofonlinenews.com | 2011 | English | JAR | news | split images[ref][ref]. Later legit. | |
| 207.210.250.131 | starrynightnews.com | 2011 | Arabic | JS | news | interesting design | |
| 207.210.250.132 | aeronet-news.com | 2011 | English | JAR | airplanes | ||
| 207.210.250.133 | bakaribulletin.com | 2011 | English | Africa | JS | news | Bakari could either be a given name, or a village in Togo |
| 207.210.250.134 | deprensaenlarevisiondehoy.com | 2011 | Spanish | JAR | news | ||
| 207.210.250.135 | icwb-news.com | 2011 | English | JAR | news | ICWB stands for "Inner Circle Worldwide Business (News)", the title of the website | |
| 207.210.250.136 | sportsreelhighlights.com | 2011 | English | JAR | sports | ||
| 207.210.250.138 | inquiry-human-past.com | 2011 | English | JAR | history | ||
| 207.210.250.139 | thefairwaysaregreen.com | 2011 | Thai | JAR | sports, golf | ||
| 207.210.250.142 | russiaupdate.com | 2011 | Russian | news | Older unrelated archive: web.archive.org/web/20010429003443/http://russiaupdate.com/. Visible but possibly cut title "Россия Обновление" (Russia Update) | ||
| 207.210.250.143 | archaeologyreview.net | 2010 | English | JAR | history, archeology | ||
| 207.210.250.146 | noticias-caracas.com | 2011 | Spanish | Venezuela | CGI | news | Caracas is the capital of Venezuela. But you knew that, right? |
| 207.210.250.147 | bailandstump.com | 2011 | English | JS | sports, cricket | "Bail" and "Stump" are the two parts of the thing your're supposed to hit with the ball in cricket.[ref] | |
| 207.210.250.148 | classicalmusic4arab.com | 2011 | music | The first words in the title are "كلاسيكيات الموسيقى العربية" (Arabic music classics) | |||
| 207.210.250.149 | globalventurestat.com | 2008 | English | SWF | news | ||
| 207.210.250.152 | al-rashidrealestate.com | 2010 | Arabic | Egypt | CGI | finance, real-estate | |
| 207.210.250.153 | newsintheworld-ru.com | 2011 | Russian | JAR | news | ||
| 207.210.250.154 | news-unlimited.info | 2011 | English | news | "members" link visible so likely GI comms. | ||
| 208.93.112.105 | fastnews-online.com | 2009 | English | JAR | news | a.newslink | |
| 208.93.112.106 | travelxtreme.net | 2008 | English | JAR | travel | split images | |
| 208.93.112.108 | nbanewsroundup.com | 2013 | English | CGI | sports, basketball | quite broken with only HTML archived in 2013, but we're counting it due to coms link and IP range. cqcounter.com/whois/www/nbanewsroundup.com.html shows it well. | |
| 208.93.112.110 | luxuryfive.net | 2011 | English | travel | Title: "Luxury five" | ||
| 208.93.112.111 | topfootballnewsonline.com | 2011 | English | sports, footbal | "Top Football News Online". | ||
| 208.93.112.112 | todaysportscores.com | 2011 | English | sports | |||
| 208.93.112.114 | dynamicworldnews.com | 2011 | English | news | |||
| 208.93.112.116 | gazingvoyage.com | 2011 | English | travel | |||
| 208.93.112.123 | garundipost.com | 2011 | English | news | TODO meaning of "Garundi" | ||
| 208.254.38.39 | todaysengineering.com | 2011 | English | CGI | engineering | ||
| 208.254.38.56 | nejadnews.com | 2011 | Arabic | JAR | news | rss, JAR unarchived | |
| 208.254.40.96 | sixty2media.com | 2011 | English | Various | JAR | news | Epoch times link |
| 208.254.40.99 | newspoliticssource.com | 2013 | Arabic | JAR | news | One of the news mentions Snowden | |
| 208.254.40.110 | musical-fortune.net | 2010 | English | CGI | music | images /images/banner-02.jpg | |
| 208.254.40.113 | ashoka-gemstones.com | 2010 | English | JAR | jewelry | ||
| 208.254.40.117 | worldnewsandent.com | 2010 | Arabic | Egypt | CGI | mews | |
| 208.254.40.124 | riskandrewardnews.com | 2013 | English | CGI | finance | ||
| 208.254.42.194 | it-proonline.com | 2011 | English | CGI | tech | images /images/header_01.jpg | |
| 208.254.42.205 | driversinternationalgolf.com | 2011 | English | CGI | sports, golf | ||
| 208.254.42.209 | mardelsurnoticias.com | 2011 | Spanish | JAR | news | weird mixture of Portuguese and Spanish language external links | |
| 208.254.42.215 | nowfreshfinances.com | 2011 | English | CGI | finance | CGI unarchived | |
| 208.254.42.216 | circulatingnews.net | 2010 | English | JAR | travel | ||
| 208.254.42.219 | westingtonpassnews.com | 2011 | English | JAR | news | ||
| 209.162.192.44 | thejewelofsouthamerica.com | 2010 | Spanish | CGI | nature, birds | rss-item, split images. CGI unarchived but likely under the "Foro" (Forum) link. Talks about the Amazon river and rainforest which it refers to in the Spanish title of the English domain: "La Joya de Sudamerica" (The Jewl of South America). | |
| 209.162.192.49 | rastadirect.net | 2010 | English | JAR | fansite | ||
| 209.162.192.51 | yellow-chair-report.com | 2011 | English | CGI | news | rss-item, split images. CGI unarchived likely under "Members" link. | |
| 209.162.192.57 | globalnewsreports.net | 2010 | English | CGI | news | rss-item. Copyright 2008. CGI unarchived. Comms unarchived likely CGI under "Forum" link | |
| 209.162.192.59 | easytravelsite.net | 2009 | English | CGI | news | Split headers. CGI unarchived, likely under "Login" link. | |
| 209.51.136.178 | cellar-notes.com | 2011 | English | JAR | wine | rss, split images, JAR unarchived | |
| 209.51.136.178 | the-news-scene.com | 2011 | English | JAR | news | split images, RSS | |
| 210.80.75.36 | e-commodities.net | 2011 | English | JAR | finance | ||
| 210.80.75.37 | trekkingtoday.com | 2011 | English | JAR | sports, running | split images[ref][ref]. rdns source. | |
| 210.80.75.41 | multinews-33.com | JAR | news | No archives of the HTML, but the JAR was archived | |||
| 210.80.75.43 | gulfandmiddleeastnews.com | 2011 | Arabic | JS | news | ||
| 210.80.75.44 | whirlybirdinflight.com | 2011 | English | JAR | helicopters | ||
| 210.80.75.45 | kings-game.net | 2011 | English | JAR | gaming, chess | JAR unarchived | |
| 210.80.75.46 | topglobalnewsdaily.com | 2011 | English | JS | news | ||
| 210.80.75.49 | recipe-dujour.com | 2011 | English | JAR | cooking | nice design | |
| 210.80.75.53 | sportsman-elite.com | 2011 | English | sports | |||
| 210.80.75.55 | philippinenewsonline.net | 2010 | Philippines | JAR | news | ||
| 210.80.75.56 | technewsforme.com | 2011 | Farsi | JAR | tech | ||
| 210.80.75.59 | goldeportesnoticias.com | 2011 | Spanish | sports, football | |||
| 212.4.16.224 | lanoticiasdehoyelinforme.com | 2010 | Spanish | JAR | news | ||
| 212.4.16.232 | mynewscheck.com | 2011 | English | Canada | JAR | news | rdns source |
| 212.4.16.245 | financial-crisis-news.com | 2011 | Russian | Russia | JAR | news | rdns source |
| 212.4.16.252 | minutosdenoticias.com | 2010 | Spanish | CGI | news | CSS | |
| 212.4.17.38 | fightwithoutrules.com | 2011 | Russian | JAR | sports, combat sports | The photo on top middle can be seen e.g. at spfightingtalk.wordpress.com/2013/01/18/breaking-down-mixed-martial-arts-what-is-mma/. The fither on top is Mac Danzig, TODO find bottom one lazy now. | |
| 212.4.17.41 | newtechfrontier.com | 2010 | English | CGI | tech | since became legit: newtechfrontier.com/ | |
| 212.4.17.43 | smart-travel-consultant.com | 2011 | Chinese | CGI | travel | ajaxtax.js may be of interest for fingerprinting. Title: "智能旅行顾问", lit. Smart Travel Consultant | |
| 212.4.17.46 | atentlaloc.com | 2009 | English | Quatar, Lebanon, Israel, Iran | JS | jewelry | Tlaloc is an Aztec deity, and Aten is an Egyptian deity. Both appear to be somewhat linked to gold, thus their usage in a jewelry website. Creative domain name. |
| 212.4.17.53 | newsresolution.net | 2010 | English | Côte d'Ivoire, Lebanon, Sudan | JAR | news, UN Peacekeeping | |
| 212.4.17.56 | lesummumdelafinance.com | 2010 | French | France | JAR | finance | |
| 212.4.17.98 | topbillingsite.com | 2011 | English | CGI | films | ||
| 212.4.17.122 | b2bworldglobal.com | 2011 | English | CGI | news | ||
| 212.4.17.125 | worldaroundyunnan.com | 2011 | Chinese | JAR | news | rss, split images, JAR | |
| 212.4.17.160 | localtoglobalnews.com | 2010 | English | JAR | news | rss, split images | |
| 212.4.18.14 | football-enthusiast.com | 2011 | English | Europe | JS | sports, football | |
| 212.4.18.129 | sightseeingnews.com | 2010 | English | JAR | travel | ||
| 212.209.74.105 | globalbaseballnews.com | 2011 | English | JS | sports, baseball | ||
| 212.209.74.106 | football-de-luxe.com | 2010 | French | France | JAR | sports, football | |
| 212.209.74.112 | developmental-league.com | 2010 | English | CGI | sports, American football | CGI comms variant? | |
| 212.209.74.115 | mediocampodefutbol.com | 2010 | Spanish | JAR | sports, football | ||
| 212.209.74.117 | myengineeringaffinity.com | 2011 | English | JAR | tech | ||
| 212.209.74.122 | atthemovies.biz | 2011 | English | JAR | cinema | Archive very broken with no text and rather only images in a table. But it has a link to unarchived JAR. The only .biz domain found so far as of writing. There are also some broken redirect archives from 2003. | |
| 212.209.74.123 | worldfinancialexchangenews.com | 2010 | English | SWF | finance | SWF unarchived. | |
| 212.209.74.124 | urouttahere.com | 2011 | English | Travel | The title means "you're out of here", a reference to this being a travel website. A closely stock image of the same child models is visible at: www.hammockbeach.com/play/kids-crew-resort-program/ | ||
| 212.209.74.125 | avoilurefixe.com | 2011 | French | Tunisia | JAR | airplanes | "à voilure fixe" is French for "with fixed wing", i.e. fixed wing aircraft |
| 212.209.74.126 | headlines2day.com | 2011 | Farsi | JAR | news | marked copyright 2009 | |
| 212.209.79.34 | fgnl.net | 2011 | English | Iran | CGI | news | four letter domain! FGNL stands for "Farsi Global News Links" Marked copyright 2009. |
| 212.209.79.37 | fitness-sources.com | 2010 | English | JS | sports, fitness | ||
| 212.209.79.40 | hydradraco.com | 2011 | English | JAR | sports, American football | TODO meaning of the name? | |
| 212.209.79.41 | noticiasdelmundolatino.com | 2011 | Spanish | JAR | news | ||
| 212.209.79.42 | suparakuvi.com | 2011 | French | France | JAR | news | a Tour Eiffel image, and young people stuff, i.e. first world stuff. It's for France alright. But TODO meaning of domain name? Ciro's second language French didn't cut it this time. |
| 212.209.79.46 | cetusdelph.com | 2011 | English | JS | sports, scuba | ||
| 212.209.79.47 | willtoworship.com | 2011 | English | JAR | religion, Christianity | marked copyright 2007 | |
| 212.209.79.48 | themvconnection.com | 2011 | English | JAR | music | ||
| 212.209.79.51 | pi-resources.net | 2010 | English | JS | private investigators | "pi" stands for Private Investigators. The CIA must have had some fun making this one. | |
| 212.209.79.53 | ourscubaworld.com | 2011 | English | JS | sports, scuba | ||
| 212.209.79.58 | tech-love-home.com | 2011 | Chinese | JS | tech | Title: "消费类电子产品", lit. Consummer Electronics | |
| 212.209.79.60 | first-solo-aviation.com | 2010 | English | JAR | airplanes | ||
| 212.209.79.61 | china-destinations.org | 2011 | Chinese | JS | travel | title: "中国目的地指南", lit. "China Destination Guide" | |
| 212.209.90.69 | worldedgenews.com | 2011 | English | JAR | news | ||
| 212.209.90.72 | talkingpointnews.info | 2011 | English | news | |||
| 212.209.90.74 | globalinvestmentnews.net | 2010 | English | JAR | news | rss, split images | |
| 212.209.90.75 | prebitinvestment.com | 2011 | English | finance | Title: "Pre-BIT Investment". TODO meaning of "BIT". | ||
| 212.209.90.80 | nsmovies.net | 2010 | English | JAR | films | "ns" stands for "Nirguna Saguna", two separate Hindu names/deities. But there are no other Indian references beyond those. | |
| 212.209.90.82 | middleeastjournal.net | 2010 | Arabic | JS | news | ||
| 212.209.90.84 | thenewseditor.com | 2011 | English | JAR | news | ||
| 212.209.90.87 | newsandweathersource.com | 2009 | English | JAR | news | marked copyright 2009. | |
| 212.209.90.89 | pakisports.com | 2010 | English | Pakistan | SWF | sports | |
| 212.209.90.90 | vriha-aesthetics.com | 2011 | Arabic | JS | news | ||
| 212.209.90.92 | amishkanews.com | 2011 | English | India | JS | news | Amishka is an Indian name, plus some prominent mentions of Bollywood both point to India specifically |
| 212.209.90.93 | theentertainbiz.com | 2011 | English | JAR | entertainment | ||
| 212.209.90.94 | eurosportssummary.com | 2011 | English | JAR | sports | ||
| 216.93.248.194 | esmundonoticias.com | 2011 | Spanish | JAR | news | rss-items. Shares IP with kukrinews.com. | |
| 216.93.248.194 | kukrinews.com | 2010 | English | JS | News | JavaScript with SHAs. Talks to /cgi-bin/news.cgi. A Kukri is the national weapon of Nepal. Slogan: "Nepal's Sharp Edge", thus matching the website name. Split image header. Copyright 2009. Shares IP with esmundonoticias.com. | |
| 216.93.248.194 | lasthournews.com | 2010 | Urdu | jAR | news | split images | |
| 216.93.248.194 | tech-geek-news.com | 2010 | Arabic | JS | news | Split images, rss-item. Comms unarchived. Wayback machine archive very broken but cqcounter.com/whois/www/tech-geek-news.com.html perfectly in style. | |
| 216.104.38.114 | all-sport-headlines.com | 2011 | Arabic | JAR | news | split images[ref][ref]Arabic-looking alphabet, image only so can't Google translate easily. | |
| 216.104.38.114 | wahidfutbol.com | 2011 | Arabic | JS | football | Wayback Machine very broken. cqcounter.com/whois/www/wahidfutbol.com.html somewhat in-style, but not very typical. | |
| 216.104.38.114 | wildbirds-seasia.com | 2011 | English | JAR | nature, birds | Slit headers, rss-item. "Birds of Southeast Asia". Stock image match example at: fr.pinterest.com/pin/745627282030750518/, possibly a greater bird-of-paradise. | |
| 216.105.98.132 | europeantravelcafe.com | 2010 | English | travel | rss-items, split images. Marked copyright 2009. Comms not found. There's a currency converter at: web.archive.org/web/20100724024644/http://www.europeantravelcafe.com/tools.html which could be suspicious. The "plan your trip" link links to a different website: secure-cert.net/~etc/transport.html which is unusual. A similar thing happens in intloil.org. That link was removed from the next archive: web.archive.org/web/20110201192245/http://europeantravelcafe.com/ which is quite funny, looks like a bug and is possibly a link used by the CIA operators to manage the website? "secure-cert.net" is obscure, the only other surviving online mention of it is www.leewillis.co.uk/wordpress-plugins/#comment-6513 | ||
| 216.105.98.134 | fuenteneta.com | 2011 | Spanish | news | Google says: | ||
| 216.105.98.135 | ilat-news.com | 2011 | English | news | The domain stands for : "International Law Enforcement & Anti Terrorism", also on page "Law Enforcement and Anti Terrorism news". | ||
| 216.105.98.136 | etherealinspirations.net | 2011 | English | religion | Title: "Ethereal Inspirations" | ||
| 216.105.98.137 | the-news-zone.com | 2011 | English | JAR | news | There is a broken archive: web.archive.org/web/20130814194744/http://the-news-zone.com/ which contains just the middle frame. But by chance the broken JAR link was there further confirming the hit! | |
| 216.105.98.139 | cultura-digital.net | 2008 | Spanish | CGI | news | Marked copyright 2008. Previously legit. | |
| 216.105.98.140 | uaeshoppingspree.com | 2013 | English | UAE | JAR | shopping | Archive quite broken, but has link to unarchived JAR. Has an unusually personal touch "As you can probably tell from the title of my website, shopping is my very favorite pastime." cqcounter.com/whois/www/uaeshoppingspree.com.html shows it well. |
| 216.105.98.144 | garanziadellasicurezza.com | 2011 | Italian | JAR | commercial | The archive is quite broken with toplevel archiving a frame rather than the actual website. JAR unarchived. web.archive.org/web/20110822020341/http://www.garanziadellasicurezza.com:80/news.html has rss-item. I'm counting this one it's too much. | |
| 216.105.98.145 | montanismoaventura.com | 2012 | Spanish | Spain | JS | sports, mountaineering | JS unarchived. Marked copyright 2010. More visible archive at: cqcounter.com/whois/www/montanismoaventura.com.html |
| 216.105.98.146 | large-format-news.com | 2011 | English | photography | |||
| 216.105.98.147 | nepalnewsbrief.com | 2008 | English | Nepal | JAR | news | Marked copyright 2006 (!) Registered 2007-01-18. |
| 216.105.98.148 | teclafinance.com | 2011 | Chinese | finance | CQ Counter screenshot rather broken but in a similar way as another Chinese website: cqcounter.com/whois/site/activegaminginfo.com.html so it seems that simply their screenshot mechanism of the time didn't have proper Chinese encoding support. The title is "特科拉财经" which Google Translate translates to "Tekola Finance", the first word apparently being the phonetic transliteration of a foreign name, but it is unclear what it references exactlyh. | ||
| 216.105.98.149 | entreman.com | 2011 | Englsh | CGI | business | Comms unarchived. Marked Copyright 2011. Archive a bit broken, original styling more clearly visible at: cqcounter.com/whois/www/entreman.com.html. Tis is the only website found so far that stores its custom fonts on the site e.g. /M-1c-fontfacekit/mplus-1c-black-webfont.svg. Stock of office workers at: www.shutterstock.com/image-photo/presentation-business-people-working-office-2-4767229 by Marcin Balcerzak. Light bulb stock at: www.bigstockphoto.com/image-4406416/stock-photo-money-light by PhilipO. | |
| 216.105.98.152 | modernarabicnews.com | 2013 | Arabic | JAR | news | HTML archive quite broken, but JAR was archived thankfully. cqcounter.com/whois/www/modernarabicnews.com.html shows it well. Original title: "أخبار عربية حديثة قياسي" | |
| 216.105.98.153 | global-headlines.com | 2011 | English | news | Was a legitimate WordPress website for a while in 2020. | ||
| 216.105.98.154 | everythingcricket.org | 2011 | English | JAR | sports, cricket | Also has archives from 2009, but they were a bit broken. The 2011 one is marked copyright 2011, so they actually bothered to updated that. | |
| 216.105.98.156 | familyhealthonline.net | 2011 | English | CGI | health | ||
| 216.105.98.157 | delacorne.com | 2011 | French | news | The title is french "Corne de l'Afrique Nouvelles" and "de la Corne", the French name for the Horn of Africa. So French but not France. | ||
| 216.105.98.158 | econfutures.com | 2011 | English | finance | Africa focus. Stock image source: www.istockphoto.com/photo/asian-helpdesk-support-operator-gm147050715-12052374 by imabase | ||
| 219.90.61.110 | surya-brahma.com | 2011 | Spanish | JAR | news | Surya and Brahman are Hindu concepts, but the website appears to have nothing to do with India or Hinduism. Interesting. | |
| 219.90.61.111 | classicalmusicboxonline.com | 2010 | English | CGI | music | ||
| 219.90.61.116 | athletepro.net | 2010 | English | JAR | sports | ||
| 219.90.61.117 | lajornadanow.com | 2010 | Spanish | JAR | news | ||
| 219.90.61.119 | aviation-navigation.com | 2011 | English | aviation | |||
| 219.90.61.120 | theinternationalworld.com | 2011 | English | JAR | news | rdns source. rss-items. | |
| 219.90.61.121 | thepyramidnews.com | 2011 | Farsi | Iran | JAR | news | |
| 219.90.61.122 | iran-newslink-today.com | 2011 | Farsi | Iran | JAR | news | |
| 219.90.61.123 | journeystravelled.com | 2011 | English | JAR | travel | ||
| 219.90.62.229 | information-junky.com | 2011 | English | Ghana | JAR | news | |
| 219.90.62.231 | todosperuahora.com | 2011 | Spanish | Peru | CGI | news | |
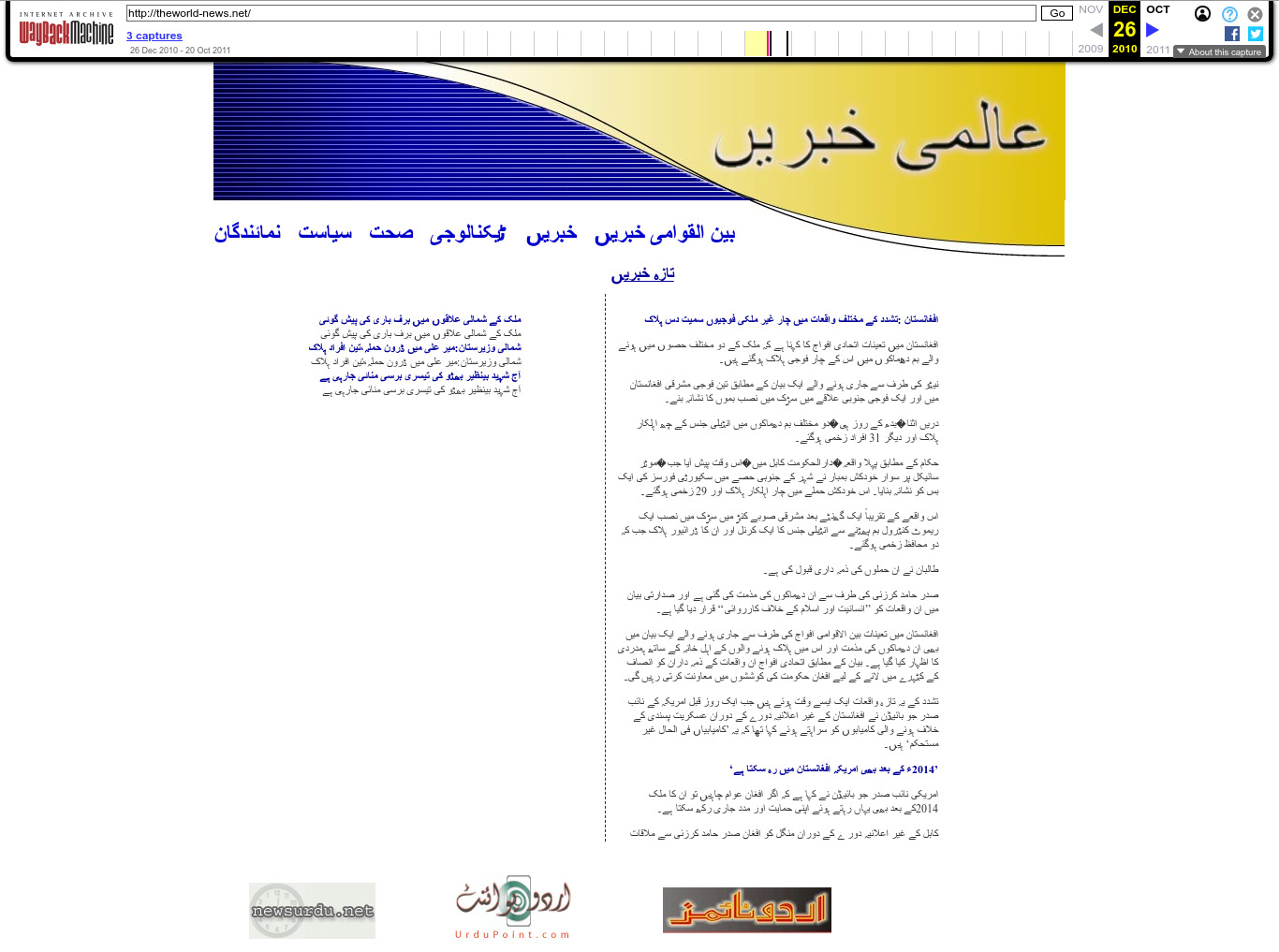
| 219.90.62.233 | theworld-news.net | 2010 | Urdu | CGI | news | ||
| 219.90.62.234 | recuerdosdeviajeonline.com | 2011 | Spanish | SWF | travel | marked "Copyright 2009" | |
| 219.90.62.235 | ordenpolicial.com | 2011 | Spanish | Spain | news, security | ||
| 219.90.62.237 | elcorreodenoticias.com | 2011 | Spanish | Venezuela | JAR | news | |
| 219.90.62.238 | freshtechonline.com | 2011 | English | CGI | tech | ||
| 219.90.62.240 | cityworldnewsnow.com | 2011 | English | news | Has subdomain secure.cityworldnewsnow.com so likely CGI comms. in-style, arab world mentions. | ||
| 219.90.62.241 | newscentertoday.com | 2011 | English | JAR | news | Copyright 2008. rdns source. rss-items. Later legit. In 2016: The domain name you have entered is not available. It has been taken down because the email address of the domain holder (Registrant) has not been verified.. | |
| 219.90.62.242 | ride-captain.com | 2011 | English | JAR | sports, motorcyles | ||
| 219.90.62.243 | fitness-dawg.com | 2021 | English | JAR | sports, fitness | Original Reuters article sample. Pushup dude stock: www.istockphoto.com/photo/sweating-young-man-doing-push-ups-gm115455429-645125 by Mike R. Manzano, pinged at: x.com/cirosantilli/status/1899750172260806711. Dude was an ex-Sr. Software engineer at Coinbase from 2019-2022, he likely retired with the Bitcoin boom already legend. Still making apps as of 2024 though: www.facebook.com/leftspin. Dog at: www.istockphoto.com/photo/english-bulldog-gm92095947-2629950 by GlobalP. | |
| 219.90.62.244 | easytraveleurope.com | 2012 | English | JAR | travel | nice design | |
| 219.90.62.245 | world-news-now.net | 2011 | English | JAR | news | ||
| 219.90.62.246 | negativeaperture.com | 2011 | English | CGI | photography | nice domain name | |
| 219.90.62.247 | conquermstoday.com | 2011 | English | CGI | health | MS means multiple sclerosis. Comms not found, CGI from unarchived subpage assumed. Has a subdomain "heal.conquermstoday.com" according to 2013 DNS Census, but no links to it in the archive. |
This section contains some of the most interesting and a few representative screenshots of the websites found.
We intentionally omit the screenshots already reported by the Reuters article.
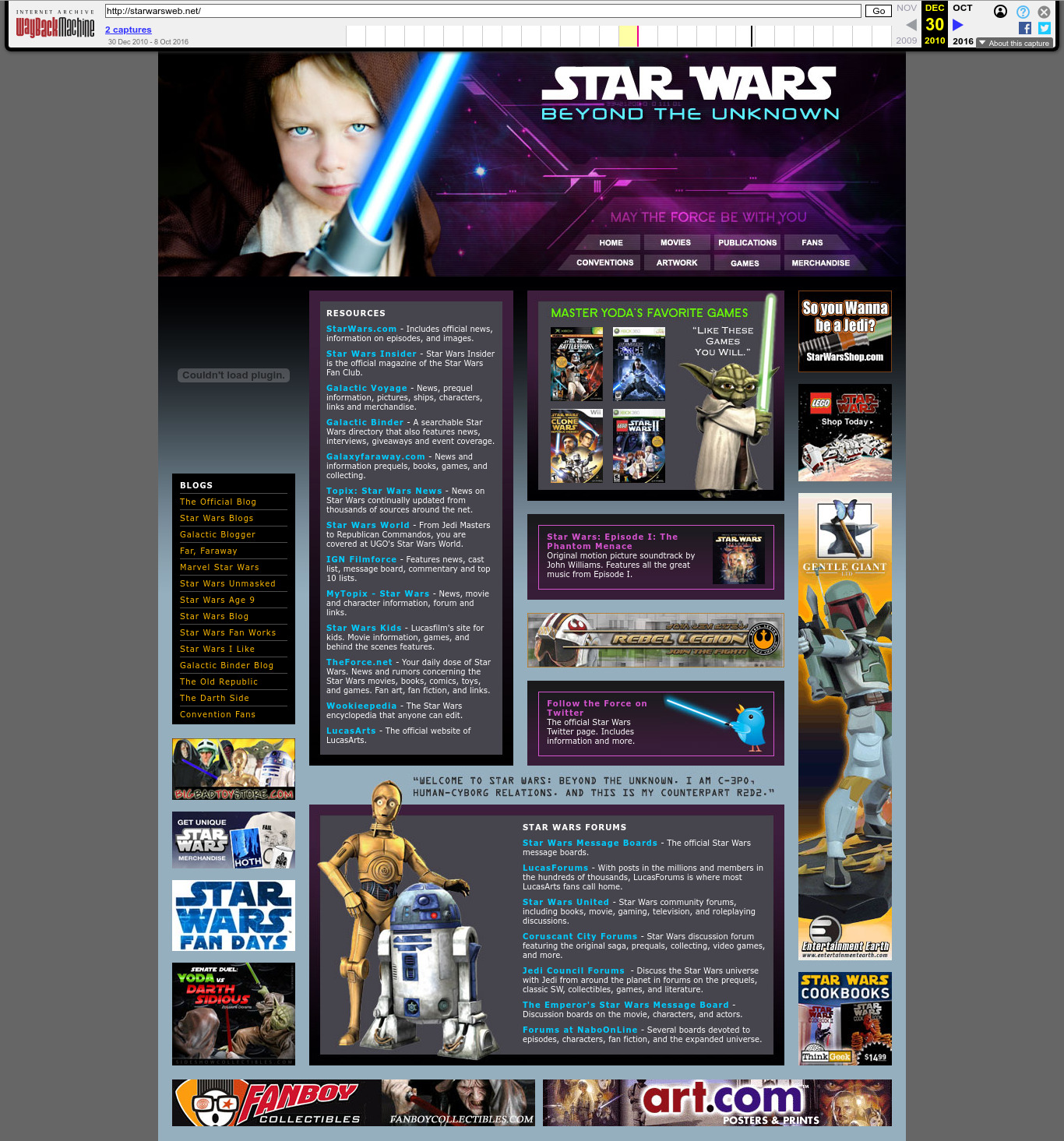
2010 Wayback Machine archive of starwarsweb.net
. The Star Wars one. Clearly branded websites like this are rare, which makes finding them all the much more fun. The Reuters article had two of them (Carson and rastadirect.net), so these were probably manually selected from the full hit dataset, and did not serve specifically as entry points. Most of the websites are quite boring and forgetful as you'd expect.
The subtitle "Beyond The Unknown" may be a reference to the Unknown Regions, an unexplored area of the galaxy in the Star Wars fictional universe.
The photo can still be licensed today as of 2025: www.gettyimages.co.uk/detail/photo/little-jedi-royalty-free-image/172984439. We found it by searching for "jedi boy" on gettyimages.co.uk. The photo is credited to a
madisonwi, presumably an alias based on the location Madison, Wisconsin. Here's a random website about adoption that uses it: www.adoptionadvocates.net/star-wars-adoption-language/ and where it can be seen without the watermarks.It later ocurred to Ciro Santilli that perhaps Reuters chose not to showcase this website because it features the photograph of a minor. But Ciro is sure that that minor is now a handsome young man in his 20's and would find the entire story very amusing if he ever finds out about it!
The images of the droids can be seen e.g. at: www.amazon.co.uk/04-Kampf-Droiden-Superheftig-Jedi/dp/B004TINSW6, a promotional material for a 2008 The Clone Wars television series audio CD and available as transparent PNGs without background in several sources. The Yoda art also seems to come from that show: rpggamer.org/page.php?page=4229.
One can almost picture the contractor who made that site seeing his children watching that show or playing the video game one evening, when a lightbulb popped over their head: tomorrow I'm going to have some fun at work.
In retrospect however, this website was likely a bad idea, since the massive pop culture appeal of Star Wars meant that when The CIA Secretly Ran a Star Wars Fan Site by Joseph Cox was published in 2025 the combination of "CIA" and "Star Wars" on a single sentence produced an irresistible clickbait that amplified knowledge of the fiasco to general public in a way that poor Johnny Carson and Bob Marley could never do. That's why you just can't have fun while working for the secret services anymore.
2011 Wayback Machine archive of alljohnny.com
. Source. Although alljohnny.com is one of the original Reuters examples, we are highlighting this screenshot here because the Reuters provided screenshot is from the extremely early 2004 version of the site, and it is interesting to see how this unique example was later updated in this 2011 version, the only known such case so far. The lack of OPSEC awareness is mind blowing, them reusing a domain like that after so many years in a completely new threat environment and possibly for a new asset.2011 Wayback Machine archive of webofcheer.com scrolled to show Johnny Carson
. Source. This website is a fansite for various comedians. It is the second known reference to Johnny Carson after alljohnny.com, which was one of the original screenshots given in the Reuters article. There must have been some massive Johnny Carson fan among the CIA contractors a that time!2011 Wayback Machine archive of iranfootballsource.com
. The third Iranian football on top of the two other published by Reuters: iraniangoalkicks.com and iraniangoals.com! Admittedly, this one is the most generic and less well designed one. But still. They pushed the theme too far!
The goalkeeper can be seen at: www.pixtastock.com/illustration/7323632.
2010 Wayback Machine archive of dedrickonline.com
. The German one.
The CIA has had a few Germany espionage scandals in the 2010s:
- 2014 www.bbc.co.uk/news/world-europe-28243933: a German Intelligence Agency agent was arrested for spying for the CIA
- 2021 www.reuters.com/world/europe/us-security-agency-spied-merkel-other-top-european-officials-through-danish-2021-05-30/ U.S. spied on Merkel and other Europeans through Danish cables
- 2020 www.dw.com/en/how-the-uss-cia-and-germanys-bnd-spied-on-world-leaders/a-52358527 it was revealed that Germany and the USA had an agreement to spy on world leaders, notably via compromised Swiss company Crypto AG
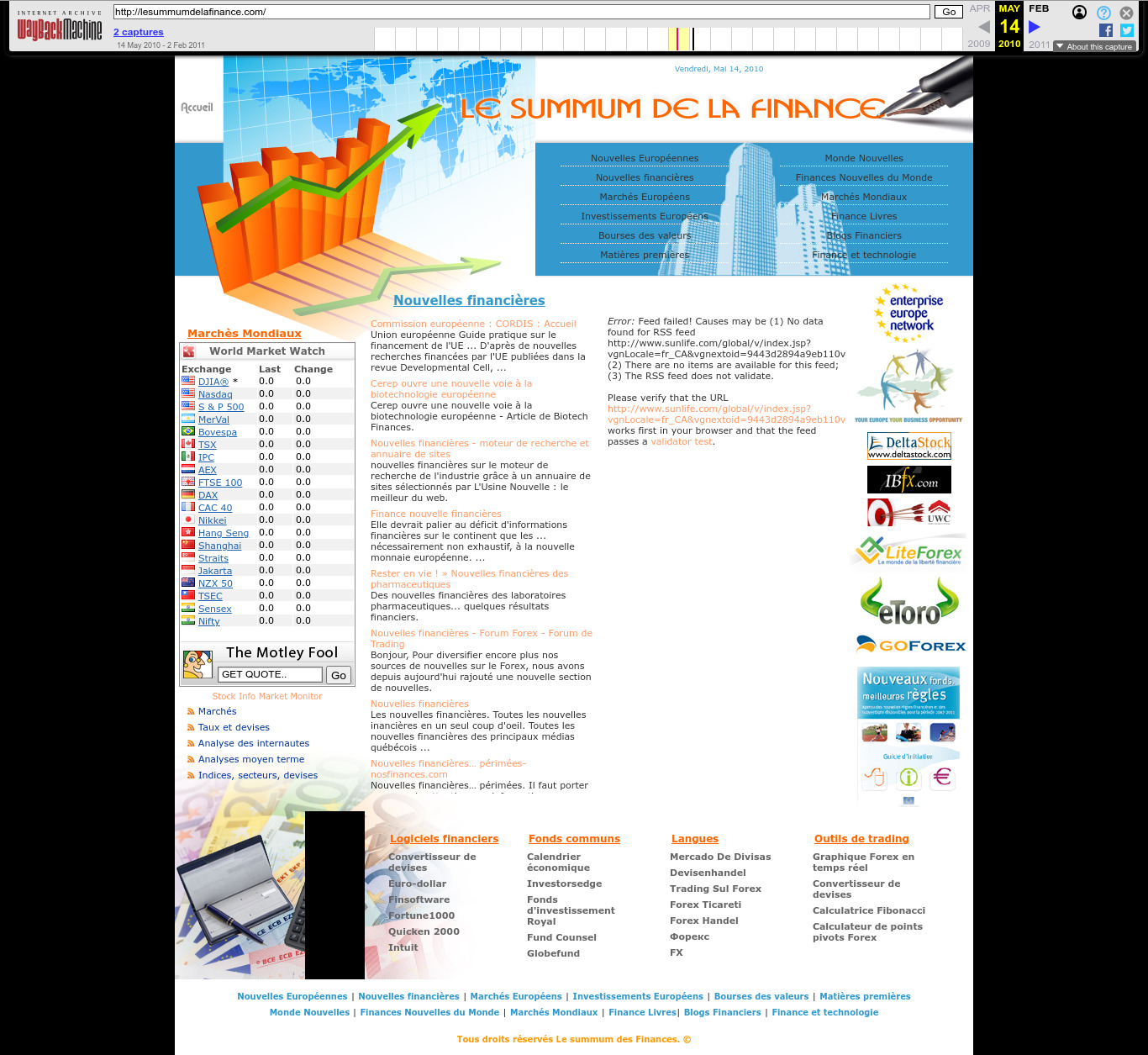
2010 Wayback Machine archive of lesummumdelafinance.com
. The arrow graph is very popular can be seen at: www.financialexpress.com/money/top-4-global-market-risks-for-2024-that-may-impact-your-finances-3346284/ and many other sites. Source unknown.
2011 Wayback Machine archive of economicnewsbuzz.com
. The Korean one. Love the kawaii style!2011 Wayback Machine archive of snapnewsfront.net
. The Japanese one.
The geisha can be seen at: www.shutterstock.com/image-vector/pretty-geisha-16813348 by Larisa Frelke, assumed accounts: x.com/larra_vit | www.xing.com/profile/Larisa_Frelke
2010 Wayback Machine archive of philippinenewsonline.net
. The Philippine one one.2011 Wayback Machine archive of feedsdemexicoyelmundo.com
. The Mexican one.2012 Wayback Machine archive of easytraveleurope.com
. 2011 Wayback Machine archive of tee-shot.net
. One of the many golf-themed sites. Golf appears to be quite popular over in Langley. It's exactly what you'd expect for a mid-level spook to do in their free time!2011 Wayback Machine archive of nouvellesetdesrapports.com
. 2011 Wayback Machine archive of pangawana.com
. 2011 Wayback Machine archive of recuerdosdeviajeonline.com
. 2011 Wayback Machine archive of theworld-news.net
. 2011 Wayback Machine archive of kessingerssportsnews.com
. 2011 Wayback Machine archive of negativeaperture.com
. Some less-trivial breakthroughs:
- finding 2013 DNS Census
- CGI comms characterization
- secure subdomain search on 2013 DNS Census let to a few hits
- 2013 DNS Census virtual host cleanup heuristic keyword searches was massive and led to many new ranges
Scrapped justdropped data, patched:and then:
+++ b/cia-2010-covert-communication-websites/cdx-post.sh
@@ -1,7 +1,7 @@
#!/usr/bin/env bash
# Post process the output of cdx.sh to enrich IDs even further, and reconstruct easier to Web Archive inspect domain names.
-grep -P -e '([^,)]+)\)\/\1\.swf|\)/[^/]+.jar|([^,)]+),([^,)]+),([^,)]+)\)/cgi-bin/[^/]+\.cgi' "$1" |
- sed -r 's/\).*//' | awk -F, '{ printf("%s.%s\n", $2, $1) }' | uniq -c | awk '$1 == 1{ print $2 }' | tee $1.post
+grep -P -e '([^,)]+)\)\/\1\.swf|\)/[^/]+.jar|([^,)]+),([^,)]+),([^,)]+)\)/cgi-bin/[^/]+\.cgi' "$1"|
+ sed -r 's/\).*//' | awk -F, '{ printf("%s.%s\n", $2, $1) }' | uniq -c | awk '{ print $2 }' | tee $1.post./hupo-cdx-tor.sh out 'news|headline|internationali|mondo|mundo|mondi|iran|today' 2006 2022web.archive.org/web/20110203041325/http://financecentraltoday.com/
- viewdns.info/iphistory/?domain=financecentraltoday.com
- 208.91.197.27 British Virgin Islands CONFLUENCE-NETWORK-INC 2013-11-08
- 69.90.163.85 Canada COGECO-PEER1 2013-09-26
- 69.90.160.75 Canada COGECO-PEER1 2011-06-22 viewdns.info/reverseip/?t=1&host=69.90.160.75 says small virtual. Checked all but no hits.
- securitytrails.com/domain/financecentraltoday.com/history/a
- 69.90.160.75 Aptum Technologies 2010-04-04 (15 years) 2010-04-27 (15 years) 23 days
- 69.42.58.70 Aptum Technologies 2009-01-07 (16 years) 2009-01-28 (16 years) 21 days. Near health-men-today.com.
web.archive.org/web/20110202221328/http://thenewsofpakistan.com/
- viewdns.info/iphistory/?domain=thenewsofpakistan.com
- 50.22.27.227 Dallas - United States SOFTLAYER 2013-06-30
- 174.133.70.18 United States SOFTLAYER 2012-11-12. In range.
- securitytrails.com/domain/thenewsofpakistan.com/history/a
web.archive.org/web/20110201184753/http://shadesofnews.com/
- viewdns.info/iphistory/?domain=shadesofnews.com
- 64.6.225.2 United States WEBINT 2013-11-29 viewdns.info/reverseip/?t=1&host=64.6.225.2 mid virtual.
- securitytrails.com/domain/shadesofnews.com/history/a
web.archive.org/web/20050424123432/http://www.pokernewsweb.com/ likely legit in the intended emulated style
web.archive.org/web/20101226225311/http://world-news-online.net/ domainsbyproxy.com registered 2006-06-14T21
- viewdns.info/iphistory/?domain=world-news-online.net
- 199.187.208.12 Miami - United States PERFORMIVE 2013-12-02 viewdns.info/reverseip/?t=1&host=199.187.208.12 is small virtual, checked all in there and 199.187.208.5 - 199.187.208.15
- 63.247.81.241 United States NTHL 2011-09-07 viewdns.info/reverseip/?t=1&host=63.247.81.241 searching 63.247.81.249
- 63.247.81.241 web.archive.org/web/20110202210855/http://motornstyle.com/ off
- 63.247.81.244 web.archive.org/web/20110106222053/http://puzzlesgalore.net/ under construction
- 63.247.81.245 web.archive.org/web/20110202102921/http://chairyogavideo.com/ under construction
- 63.247.81.247 web.archive.org/web/20110207131727/http://pccubeservice.com/indexPage.jsp
- securitytrails.com/domain/world-news-online.net/history/a
web.archive.org/web/20100923090646/http://mideasttoday.net/
- viewdns.info/iphistory/?domain=mideasttoday.net says:
- 208.91.197.27 British Virgin Islands CONFLUENCE-NETWORK-INC 2013-12-09
- 65.98.118.97 United States FORTRESSITX 2013-12-02
- 65.98.118.101 United States FORTRESSITX 2013-05-20. viewdns.info/reverseip/?t=1&host=65.98.118.101 empty
- securitytrails.com/domain/mideasttoday.net/history/a says:
web.archive.org/web/20110209045123/http://dryterrainnews.com/
- viewdns.info/iphistory/?domain=dryterrainnews.com says:
- 50.22.27.227 Dallas - United States SOFTLAYER 2013-11-29
- 174.133.70.18 United States SOFTLAYER 2012-11-12
- securitytrails.com/domain/dryterrainnews.com/history/a
web.archive.org/web/20100206221718/http://euronewsonline.net/
- viewdns.info/iphistory/?domain=euronewsonline.net says:
- 74.220.207.94 United States UNIFIEDLAYER-AS-1 2013-12-09
- 184.168.221.55 United States AS-26496-GO-DADDY-COM-LLC 2013-11-25
- 74.220.207.94 United States UNIFIEDLAYER-AS-1 2013-09-23. viewdns.info/reverseip/?t=1&host=74.220.207.94 says medium virtual.
- securitytrails.com/domain/euronewsonline.net/history/a also says
web.archive.org/web/20110208063146/http://news-and-sports.com/ Hit.
- viewdns.info/iphistory/?domain=news-and-sports.com says:
- 204.11.56.25 British Virgin Islands CONFLUENCE-NETWORK-INC 2014-07-05
- 208.91.197.19 British Virgin Islands CONFLUENCE-NETWORK-INC 2013-05-20
- 66.104.175.42 United States XO-AS15 2012-06-29 In range.
web.archive.org/web/20110202054628/http://intoworldnews.com/ hit.
- viewdns.info/iphistory/?domain=intoworldnews.com says:
- securitytrails:
web.archive.org/web/20110207171340/http://mydailynewsreport.com/ hit
- viewdns.info/iphistory/?domain=mydailynewsreport.com says
- 208.91.197.132 British Virgin Islands CONFLUENCE-NETWORK-INC 2014-03-15
- 74.52.51.139 United States SOFTLAYER 2012-06-29 viewdns.info/reverseip/?t=1&host=74.52.51.139 says small virtual
On that same IP...- web.archive.org/web/20110208004005/http://networkconnectionsite.com/ Hit. viewdns.info/iphistory/?domain=networkconnectionsite.com says only at that IP.
- web.archive.org/web/20110207103008/http://soccerguidesite.com/ Korean site, would be unusual given a splash page. Has a JAR at: web.archive.org/web/20110207103045/http://soccerguidesite.com/tools.jar but everything else unarchived. JAR is atypical.
Around checked 74.52.51.133 - 74.52.51.149- viewdns.info/reverseip/?t=1&host=74.52.51.136 large virtual
- securitytrails.com/domain/mydailynewsreport.com/history/a says
- 74.52.51.139 SoftLayer Technologies Inc. 2011-03-06 (14 years) 2011-03-21 (14 years) 15 days
- 174.123.39.202 SoftLayer Technologies Inc. 2010-12-08 (14 years) 2011-03-05 (14 years) 3 months
- 75.125.247.170 SoftLayer Technologies Inc. 2010-02-20 (15 years) 2010-05-22 (15 years) 3 months
- 205.178.189.129 Network Solutions, LLC 2010-02-10 (15 years) 2010-02-20 (15 years) 10 days. viewdns.info/reverseip/?t=1&host=205.178.189.129 is large virtual.
web.archive.org/web/20050508220858/http://www.asianewsupdate.com/ this looks like the exact format of legitimate site the CIA was emulating. Copyright 2005, a CGI link to as: www.asianewsupdate.com:80/cgi-sys/FormMail.cgi There's a phone there 01 647-0910 so seems less likely?
2010. JAR unarchived. rss, split image
- viewdns.info/iphistory/?domain=newsdelivered.net says:
- 192.96.218.41 United States 123NET 2013-06-10
- 196.40.84.210 Costa Rica RADIOGRAFICA COSTARRICENSE 2013-05-20
- 50.63.202.40 United States AS-26496-GO-DADDY-COM-LLC 2013-04-08
- 74.220.207.158 United States UNIFIEDLAYER-AS-1 2013-03-11. viewdns.info/reverseip/?host=74.220.207.158&t=1 says large virtual.
- securitytrails:
2010. JAR. Split header.
- viewdns.info/iphistory/?domain=latinamericanewsbeat.com says:
- 184.168.221.34 United States AS-26496-GO-DADDY-COM-LLC 2013-03-23
- 74.91.172.195 United States INTERNAP-BLOCK-4 2012-11-12
- 76.162.90.179 United States WINDSTREAM 2011-09-08. viewdns.info/reverseip/?host=76.162.90.179&t=1 says small virtual? Explored 76.162.90.174 - 76.162.90.183.
- securitytrails.com/domain/latinamericanewsbeat.com/history/a
2011. JAR unarchived. Split header.
- viewdns.info/iphistory/?domain=inkfreenews.com says:
- 68.178.232.100 United States AS-26496-GO-DADDY-COM-LLC 2012-09-21
- 128.121.9.46 United States NTT-LTD-2914 2012-06-29. Reverse empty. Checked: 128.121.9.43 - 128.121.9.53
- securitytrails.com/domain/inkfreenews.com/history/a
2011. JAR. a.newslink, a.newslinkalt.
- viewdns.info/iphistory/?domain=profile-news.com says:
- 68.178.232.100 United States AS-26496-GO-DADDY-COM-LLC 2012-06-29
- 199.204.248.105 United States WEBINT 2012-01-11. viewdns.info/reverseip/?host=199.204.248.105&t=1 says large virtual.
- 205.214.86.38 United States DATABANK-LATISYS 2011-08-11. viewdns.info/reverseip/?host=205.214.86.38&t=1 says small virtual.
- securitytrails.com/domain/profile-news.com/history/a
2011. Arabic. RSS.
- viewdns.info/iphistory/?domain=nejadnews.com says: 208.254.38.56 United States COLO-PREM-VZB 2012-06-29.
- viewdns.info/reverseip/?host=208.254.38.56&t=1 says single domain and we see that todaysengineering.com was not too far confirming a new range
web.archive.org/web/20110129115400/http://kmirano.com/ shallow but off style? Has a kmirano.sfw... viewdns.info/iphistory/?domain=kmirano.com says 211.1.224.71 Japan NTT SmartConnect Corporation 2012-01-11
2011. JAR. Copyright 2008. Split header and other images. They are obsessed about CDMA (2G).
- viewdns.info/iphistory/?domain=wiredworldnews.com says:
- 69.89.237.152 United States RINGSQUARED 2012-01-11. Empty.
- 67.213.209.10 Atlanta - United States UK-2 Limited 2011-04-04. Virtual.
- securitytrails.com/domain/wiredworldnews.com/history/a
- 69.89.237.152 RingSquared 2011-06-25 (14 years) 2011-07-30 (14 years) 1 month
- 69.89.237.152 RingSquared 2011-06-14 (14 years) 2011-06-24 (14 years) 10 days
- 67.213.209.10 UK-2 Limited 2008-12-03 (16 years) 2009-02-10 (16 years) 2 months
- 69.4.225.2 SoftLayer Technologies Inc. 2008-09-01 (17 years) 2008-09-09 (17 years) 8 days. viewdns.info/reverseip/?t=1&host=69.4.225.2 empty.
2011. JAR. split header, RSS.
- viewdns.info/iphistory/?domain=the-news-scene.com says 74.81.69.194 United States NTHL 2012-01-11. viewdns.info/reverseip/?host=74.81.69.194&t=1 says virtual.
- securitytrails.com/domain/the-news-scene.com/history/a says
- 74.81.69.194 NETWORK TRANSIT HOLDINGS LLC 2009-12-24 (15 years) 2010-03-23 (15 years) 3 months
- 209.51.136.178 QuickMeg Inc 2008-09-01 (17 years) 2009-12-24 (15 years) 1 year. viewdns.info/reverseip/?t=1&host=209.51.136.178 says small virtual and in there we obtain:Explored viewdns.info 209.51.136.170 - 209.51.136.185 empty.
2010. Suspicious. But no clear fingrenprint. Also not as shallow as others. Also Joomla based which would be novel.
- viewdns.info/iphistory/?domain=eqranews.com says:
- 69.64.147.243 United States RIGHTSIDE 2012-03-03
- 67.228.81.180 Seattle - United States SOFTLAYER 2011-04-04. viewdns.info/reverseip/?t=1&host=67.228.81.180 says virtual.
- securitytrails.com/domain/eqranews.com/history/a says
- 69.64.147.243 Amazon.com, Inc. 2011-04-28 (14 years) 2012-01-19 (13 years) 9 months
- 67.228.81.180 SoftLayer Technologies Inc. 2011-04-18 (14 years) 2011-04-28 (14 years) 10 days
- 174.37.172.68 SoftLayer Technologies Inc. 2011-04-13 (14 years) 2011-04-18 (14 years) 5 days
- 67.228.81.180 SoftLayer Technologies Inc. 2011-03-19 (14 years) 2011-04-13 (14 years) 25 days
- 74.220.215.62 Unified Layer 2010-03-18 (15 years) 2011-03-19 (14 years) 1 year
2010. JAR.
- viewdns.info/iphistory/?domain=magneticfieldnews.com says 173.205.124.151 United States IMH-IAD 2012-01-11. viewdns.info/reverseip/?host=173.205.124.151&t=1 says large-ish virtual.
- dnshistory.org/dns-records/magneticfieldnews.com empty
- securitytrails.com/domain/magneticfieldnews.com/history/a
2011. JAR. RSS, Split header images.
- viewdns.info/iphistory/?domain=segomonews.com 204.13.11.6 United States KATTARE 2012-01-11. viewdns.info/reverseip/?host=204.13.11.6&t=1 says virtual.
- dnshistory.org/historical-dns-records/a/segomonews.com same
- securitytrails.com/domain/segomonews.com/history/a same
newspapergateway.com/ web.archive.org/web/20110208070309/http://newspapergateway.com/ hard to tell but generally off. Has both JAR and SWF.
- viewdns.info/iphistory/?domain=newspapergateway.com says:
- 63.251.171.80 United States INTERNAP-BLOCK-4 2011-11-13
- 66.115.138.101 United States PERFORMIVE 2011-09-08
2011 Farsi. JAR. RSS.
- dnshistory.org/dns-records/pondernews.net nothing
- viewdns.info/iphistory/?domain=pondernews.net. privatesystems.net.
- 68.178.232.100 United States AS-26496-GO-DADDY-COM-LLC 2011-11-28
- 67.222.6.108 Atlanta - United States PRIVATESYSTEMS 2011-10-31. Virtual. Also here on very quick look at promising names:
- web.archive.org/web/20100517070603/http://middle-east-newstoday.com/ Only at that IP. JS.
- securitytrails.com/domain/pondernews.net/history/a
2011. English. Split header, RSS.
- viewdns.info/iphistory/?domain=internationalnewsworthiness.com says 216.86.153.116 United States STEADFAST 2011-04-04. Checking 216.86.153.106 - 216.86.153.125
- viewdns.info/reverseip/?host=216.86.153.114&t=1 big virtual
- viewdns.info/reverseip/?host=216.86.153.116&t=1 says it became a medium virtual
- dnshistory.org/dns-records/internationalnewsworthiness.com empty
- securitytrails.com/domain/internationalnewsworthiness.com/history/a
sandstormnews.com 2011, SWF Arabic.
ul.rss-items > li.rss-item, split header- viewdns.info/iphistory/?domain=sandstormnews.com
- 68.178.232.99 United States AS-26496-GO-DADDY-COM-LLC 2011-04-04. viewdns.info/reverseip/?t=1&host=68.178.232.99 says big virtual.
- securitytrails.com/domain/sandstormnews.com/history/a
zerosandonesnews.com 2011. SWF Split header,
ul.rss-items > li.rss-item- viewdns.info/iphistory/?domain=zerosandonesnews.com empty
- dnshistory.org/dns-records/zerosandonesnews.com empty
- securitytrails.com/domain/zerosandonesnews.com/history/a says 62.22.61.200 which is in range
differentviewtoday.com: web.archive.org/web/20110202185635/http://differentviewtoday.com/ split header images JAR archived at: web.archive.org/web/20110202185659/http://differentviewtoday.com/bwm.jar
lasthournews.com web.archive.org/web/20100513182623/http://lasthournews.com/. Urdu. JAR at: web.archive.org/web/20100513182724/http://lasthournews.com/recent.jar. Split header images.
- viewdns.info/iphistory/?domain=lasthournews.com no relevant IPs
- dnshistory.org/historical-dns-records/a/lasthournews.com mentions 2010-02-27 -> 2010-08-07 216.93.248.194
- securitytrails.com/domain/lasthournews.com/history/a says
mynepalnews.com, split header images,
ul.rss-items > li.rss-item, Unarchived jar:- viewdns.info/iphistory/?domain=mynepalnews.com
- 5.9.240.230 Falkenstein - Germany Hetzner Online GmbH 2014-01-31
- 142.4.222.67 Canada OVH SAS 2013-12-20
- 72.9.137.7 Nepal WorldLink Communications Pvt Ltd 2013-06-30. Big virtual.
- 64.71.179.79 United States HURRICANE 2012-11-12. Nothing else on 64.71.179.71 - 64.71.179.89.This IP address also shows up on web.archive.org/web/20110204095753/http://mynepalnews.com/cgi-bin/check.cgi/
SERVER_ADDR = 64.71.179.79There we also see:which appears to be the crawler's IP: github.com/duy13/vDDoS-Protection/issues/29REMOTE_ADDR = 204.236.235.245
- securitytrails.com/domain/mynepalnews.com/history/a
- 5.9.219.166 Hetzner Online GmbH 2013-12-31 (11 years) 2014-01-08 (11 years) 8 days
- 142.4.222.67 OVH SAS 2013-12-02 (11 years) 2013-12-31 (11 years) 29 days
- 72.9.137.7 WorldLink Communications Pvt Ltd 2013-01-24 (12 years) 2013-04-02 (12 years) 2 months
- 64.71.179.79 Hurricane Electric LLC 2008-09-01 (17 years) 2008-10-21 (16 years) 2 months
- web.archive.org/web/20111008211517/http://elgintoday.com/ wordpress so unlikely
- 50.63.202.88 United States AS-26496-GO-DADDY-COM-LLC 2014-02-21
- 97.74.249.128 United States AS-26496-GO-DADDY-COM-LLC 2014-01-11 big virtual
Announcements and updates by self:
- 2023-06-10: initial announcements
- twitter.com/cirosantilli/status/1667532991315230720. Follow up when more domains were found: twitter.com/cirosantilli/status/1717445686214504830
- www.reddit.com/r/OSINT/comments/146185r/i_found_16_new_cia_covert_communication_websites/. Marked as SPAM 5 by mods days later. After reaching 92 votes, a very positive reply for that niche sub, and being obviously on topic. Weird. Anyways, did its job and likely kicked off hackernews.
- www.facebook.com/cirosantilli/posts/pfbid04KvRbEXghJakcD4AQz4379L5oVjPZ6vrBF1Eak3p81VnqRSXuXdvvYonCWPhGfQXl
- 2023-10-26 twitter.com/cirosantilli/status/1717445686214504830: announcement by self after finding 75 more sites
- Shared by others soo after:
- www.reddit.com/r/conspiracy/comments/14705gp/cia_2010_covert_communication_websites/ failed attempt with bad link unfortunately
- 2024-01-15: twitter.com/cirosantilli/status/1747742453778559165 Oleg Shakirov's findings
- 2024-01-23: mastodon.social/@cirosantilli/111807480628392615 ipinf.ru gives 4 hits and 4 new suspects, announced at:
- 2024-09 Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects
- 2025-03-13: 44 new domains found: Section "44 new CIA websites"
- 2025-04-14: cqcounter screenshots used to confirm many new hits: Section "60 new CIA website screenshots discovered on CQ Counter"
- 2025-05-23: Section "Backing up CIA website archives for research and posterity"
Pings by self:
- 2025-03-13:
- x.com/cirosantilli/status/1900278353065894324 pings x.com/JackRhysider Jack Rhysider, host of the Darkent Diaries podcast
- x.com/cirosantilli/status/1900828210578727276 pings x.com/JennaMC_Laugh Jenna McLaughlin and x.com/zachsdorfman Zach Dorfman, authors of the 2018 Yahoo articles
- 2025-03-31 going to find random interested people on Twitter:
- 2025-05-05:
- inteltoday.org/2021/07/31/us-national-whistleblower-day-july-30-2021-i-john-reidy-declare-cia-debacle-in-iran-china/#comment-46375 pings the author Dr. Ludwig De Braeckeleer. Besides his interest in intelligence, the dude actually also won a Breakthrough Prize in Physics, holy fuck it's mind boggling.
- x.com/cirosantilli/status/1919391488422662245 pings x.com/marisaataylor Marisa Taylor, author of the 2014, McClathy DC article
- x.com/cirosantilli/status/1919859345593880812 and x.com/cirosantilli/status/1919846838850499002 pings x.com/billmarczak Bill Marczak and x.com/thezedwards Zach Edwards, technical analysts for the Reuters article
- x.com/cirosantilli/status/1919860643408007644 pings x.com/joel_schectman Joel Schectman and x.com/bozorgmehr Bozorgmehr Sharafedin authors of the Reuters article
- x.com/cirosantilli/status/1919870831758365113 pings x.com/zachsdorfman Zach Dorfman (protected account) author of the Foreign Policy article
- x.com/cirosantilli/status/1920073080363241727 pings x.com/markmazzettinyt Mark Mazzetti, x.com/nytmike Michael S. Schmidt and x.com/mattapuzzo Matt Apuzzo authors of the 2017 New York Times article. Could not find a Twitter for the fourth author Adam Goldman.
- x.com/PeteWilliamsNBC Pete Williams author of the 2018 NCB News artricle: he's retired and not active on Twitter, not going to bother pinging
Reactions by others:
- 2023-06-19: www.reddit.com/r/numberstations/comments/14dexiu/after_numbers_stations_vanished/ (30 points) off topic on that sub, but thankfully was not deleted, interesting sub topic
- 2023-10-26: Google Analytics backlink from lms.fh-wedel.de/ path unknown. Some shitty German university: en.wikipedia.org/wiki/Fachhochschule_Wedel_University_of_Applied_Sciences LMS stands for Learning management system, apparently a Moodle instance. Maybe they have some Open educational resources, but all in German so pointless
- Second wave:
- 2023-12-01: news.ycombinator.com/item?id=38492304 (65 points). Second submission but pointing to OurBigBook.com rather than cirosantilli.com: ourbigbook.com/cirosantilli/cia-2010-covert-communication-websites We take those. Reached only 65 points as of January 2024.
- 2023-12-02: buttondown.email/grugq/archive/december-2-2023/. "grugq" is the handle of a zero day dealer whose received some scrutiny in 2012 after a Forbes protile was written about him: archive.ph/7mUG5. He comments:presumably referring to DNS Census 2013.
I don’t think anyone anticipated that databases leaked by hackers would enable OSINT researchers to conduct counterintelligence investigations that rival the state security services.
- 2024-01-12: twitter.com/jeremy_wokka/status/1745657801584656564 (40k followers, mid of thread)
- 2025-04-02: www.reddit.com/r/wikipedia/comments/1kd7rzo/comment/mqoocu7/?context=3 user Gilda1234_ mentions this project in a comment to "Between 2010 and 2012, China identified and killed at least 30 CIA informants in the country" by idlikebab
- 2025-05-26 The CIA Secretly Ran a Star Wars Fan Site by Joseph Cox from 404 media, an upstart publication covering edgy digital subjects. This was likely a result of Ciro publicly pinging x.com/zachsdorfman Zach Edwards, one of the analysts for the Reuters article, at x.com/cirosantilli/status/1919846838850499002, as he is cited in the article as having done a technical review. This had a massive knowdown effect and several other media picked the story up. Ciro announcing it at:Forum threads spawned from it:Other media that picked it up:
- Reddit
- www.reddit.com/r/StarWars/comments/1kvtzwm/the_cia_secretly_ran_a_star_wars_fan_site/
- www.reddit.com/r/StarWarsEU/comments/1kvu5g8/the_cia_secretly_ran_a_star_wars_fan_site/
- www.reddit.com/r/nottheonion/comments/1kxtpw4/the_cia_secretly_ran_a_star_wars_fan_site/
- www.reddit.com/r/nottheonion/comments/1kxtpw4/comment/muu531n/A source: www.thesun.co.uk/sport/33904606/putin-spies-cristiano-ronaldo-youtube-videos-messages/
They aren’t the only ones who do stuff like this, Russian agents were using Ronaldo highlight vids on YouTube to communicate 😭
- www.reddit.com/r/nottheonion/comments/1kxtpw4/comment/muu531n/
- www.reddit.com/r/Games/comments/1kye0pj/the_cia_operated_a_network_of_gaming_sites_and/
- www.reddit.com/r/technology/comments/1kvvx48/the_cia_secretly_ran_a_star_wars_fan_site_the/
- www.reddit.com/r/realtech/comments/1kvwigb/the_cia_secretly_ran_a_star_wars_fan_site_the/
- www.reddit.com/r/conspiracy/comments/1kw991t/the_cia_secretly_ran_a_star_wars_fan_site/
- www.reddit.com/r/LowStakesConspiracies/comments/1kwbf2y/the_cia_run_a_star_wars_fansite/
- www.reddit.com/r/andor/comments/1kw587c/very_andor_the_cia_secretly_ran_a_star_wars_fan/
- www.reddit.com/r/BrasildoB/comments/1kw6qah/um_brasileiro_acaba_de_publicar_detalhes_sobre_os/
- www.reddit.com/r/mexico/comments/1kwhuqg/la_incre%C3%ADble_web_de_star_wars_que_us%C3%B3_la_cia_para/
- www.reddit.com/r/KotakuInAction/comments/1kwoch5/the_cia_ran_a_star_wars_fan_site_to_secretly/
- www.reddit.com/r/starwarscanon/comments/1kwoxoq/til_the_cia_secretly_ran_a_star_wars_fan_site/
- www.reddit.com/r/TrueAnon/comments/1kwhxmj/cia_ran_star_wars_fan_site/
- www.reddit.com/r/MauLer/comments/1kxqim9/figures/
- www.reddit.com/r/Intelligence/comments/1kwybso/cia_uses_star_wars_website_to_communicate_with/
- www.reddit.com/r/StarWarsCirclejerk/comments/1kwzeto/in_my_mind_all_last_jedi_haters_are_feds/
- www.reddit.com/r/memes/comments/1kw5x9n/the_cia_really_gets_creative_sometimes/
- www.reddit.com/r/BurnNotice/comments/1kw4b5k/the_cia_secretly_ran_a_star_wars_fan_site_for/
- www.reddit.com/r/BurnNotice/comments/1kw4b5k/comment/muemkhk/ brings up
europeangoldfinch.netfirst described in Season 2 of Prison Break in 2007.Europeangoldfinch.net was a website used by Michael Scofield that allowed the Fox River Eight to communicate with each other on its online message board
- www.reddit.com/r/BurnNotice/comments/1kw4b5k/comment/muemkhk/ brings up
- Decent tweets:
- x.com/CultureCrave/status/1927119278047727908 600k followers
- x.com/val_reloaded/status/1927349417306161165 Argentinian Twitcher 400k followers
- news.ycombinator.com/item?id=44098274 failed unfortunately
- knockout.chat/thread/72492/1
- fanlore.org/wiki/2009-2013_CIA_communications_websites
- YouTube
Video 1. . Source. 2025-05-27. 180k subs. This one focuses on talking about the games and uses this article as the mainreference. He makes that nice note that the game Star Wars Battlefront II reached all time highs in the days following the CIA releasejThe articles apparenty coincided with the reelase of Star Wars Battlefront III alpha to lukewarm reception. Video 2. Star Wars Fan Sites Are Run by THE FEDS?! by Clownfish TV. Source. 2025-05-27. 600k subs. Video didn't take off however. The channel seems to be semi dead. But it is cool to see an American with YouTube-worth eloquence going over it.Video 3. . Source. 2025-05-28. 2M subs. He's basically reading the techspot article: www.techspot.com/news/108062-cia-used-star-wars-fan-site-secretly-communicate.html. Video 5. . Source. Seytonic had previously covered Reuters article at this other video:Video 8. . Source. 2025-06-13. 12k subs. This video draws on some research from this article, citing it on the source list: docs.google.com/document/d/1k7-YoOMRTL8qKE_FoRnyvR1QDa0JTBJo_a-SRwVMEu4/edit?tab=t.0 and using some of the screenshots.This video has some good mentions of the details of Jerry Chun Shing Lee's story which Ciro Santilli was not aware of. - other voice media:
- Meneame, a Spanish Reddit: 2025-05-27 www.meneame.net/m/tecnolog%C3%ADa/increible-web-star-wars-uso-cia-espiar-espana-mexico-otros/standard
Starting on that same day someone made starwarsweb.net redirect to cia.gov at 2025-05-26T13:28:02Z: www.whois.com/whois/starwarsweb.net- "mainstream":
- www.dailymail.co.uk/news/article-14752155/CIA-fake-websites-Star-Wars-communicate-spies.html Also announcing that:
* mastodon.social/@cirosantilli/114580297330915997
* x.com/cirosantilli/status/1927373757829583344
* www.linkedin.com/posts/cirosantilli_the-cia-secretly-ran-a-star-wars-fan-site-activity-7333140418504646656-eRzq/
* www.facebook.com/cirosantilli/posts/pfbid026kssQcXm7TwAHDJ4BQ73RKFCmJRLJsT1dfRpEmZ5GZdmsp8DukaqrbefFuGDqNZvl - www.themirror.com/news/us-news/cia-uses-star-wars-website-1174874
- www.dailymail.co.uk/news/article-14752155/CIA-fake-websites-Star-Wars-communicate-spies.html Also announcing that:
- "mainstream" non-English:
- www.france24.com/fr/%C3%A9co-tech/20250528-star-wars-bourse-ou-football-les-etranges-sites-pour-les-informateurs-de-la-cia (French)
- francais.rt.com/international/121266-espionnage-cia-utilisait-sites-fans-star-wars-pour-communiquer-secretement-avec-ses-agents-etrangers RT in French, God
- www.derstandard.at/consent/tcf/story/3000000271640/die-cia-hat-heimlich-eine-star-wars-fanseite-betrieben Der Standard (Austria)
- tw.news.yahoo.com/玩家可能都用過?原來「美國中情局」cia曾營運過遊戲媒體網站掩護行動-070742215.html (Yahoo Taiwan)
- www.abc.es/internacional/cia-empleo-sitios-web-inofensivos-paginas-star-20250528171402-nt.html (Spain)
- "non-mainstream":
- www.dexerto.com/entertainment/the-cia-secretly-used-a-star-wars-fan-site-to-talk-to-spies-report-3199318/ and x.com/Dexerto/status/1927000891963363406 large-ish publication
- www.thegamer.com/star-wars-fan-website-cia-usa-government-spies-controlled/
- www.techspot.com/news/108062-cia-used-star-wars-fan-site-secretly-communicate.html This was one of the biggest hits on Google Analytics actually.
- gigazine.net/news/20250527-starwars-fan-sites-made-by-cia/ Japanese
- Wired:
- www.pcgamer.com/gaming-industry/the-cia-operated-a-network-of-gaming-sites-and-even-a-star-wars-fanpage-that-were-part-of-one-of-its-worst-ever-intelligence-catastrophes/
- www.msn.com/en-us/news/technology/the-cia-secretly-ran-a-star-wars-fan-site-to-communicate-with-spies/ar-AA1FASFY
- www.gamespot.com/articles/the-cia-once-ran-a-star-wars-fan-site-as-part-of-a-global-intelligence-effort/1100-6532045/
- www.darkhorizons.com/how-u-s-spies-used-a-star-wars-fan-page/
- gigazine.net/news/20250527-starwars-fan-sites-made-by-cia/
- Reddit
- 2025-08-01 saw another mini-trend due to The CIA Built Hundreds of Covert Websitesby Alan Macleod: www.mintpressnews.com/cia-secret-network-885-fake-websites/290325/
This then spawned some sindicated posts:and forum threads:- www.sott.net/article/500997-The-CIA-built-hundreds-of-covert-websites-Heres-what-they-were-hiding
- scheerpost.com/2025/08/02/the-cia-built-hundreds-of-covert-websites-heres-what-they-were-hiding/
- 2025-08-02 alethonews.com/2025/08/02/the-cia-built-hundreds-of-covert-websites-heres-what-they-were-hiding/ (Greek)
- 2025-08-02 popularresistance.org/the-cia-built-hundreds-of-covert-websites/
- 2025-08-04 cz24.news/alan-macleod-cia-vytvorila-stovky-tajnych-webu-globalni-spionazni-terminaly-co-vlastne-skryvaly/ (Czech)
Notable reactions to the websites themselves:
- 2022-09-29 www.reddit.com/r/soccer/comments/xrgua4/the_cia_used_a_message_board_on_a_fake_soccer/ "The CIA used a message board on a fake soccer website called "Iraniangoals.com" to communicate with Iranian spies, dozens of whom were arrested after the website was discovered." by user Carlos-Dangerzone
The third one from Cambridge after:
This is going to be the most important application of generative AI. Especially if we ever achieve good text-to-video.
Image generators plus human ranking:
- pornpen.ai/ a bit too restrictive. Girl laying down. Girl sitting. Penis or no penis. But relatively good at it
- civitai.tv/. How to reach it: civitai.tv/tag/nun/2/
www.pornhub.com/view_video.php?viewkey=ph63c71351edece: Heavenly Bodies Part 1: Sister's Mary First Act. Pornhub title: "AI generated Hentai Story: Sexy Nun alternative World(Isekai) Stable Diffusion" Interesting concept, slide-narrated over visual novel. The question is how they managed to keep face consistency across images.
The fundamental insight of Git design is: a SHA represents not only current state, but also the full history due to the Merkle tree implementation, see notably:
This makes it so that you will always notice if you are overwriting history on the remote, even if you are developing from two separate local computers (or more commonly, two people in two different local computers) and therefore will never lose any work accidentally.
It is very hard to achieve that without the Merkle tree.
Consider for example the most naive approach possible of marking versions with consecutive numbers:
Unlisted articles are being shown, click here to show only listed articles.