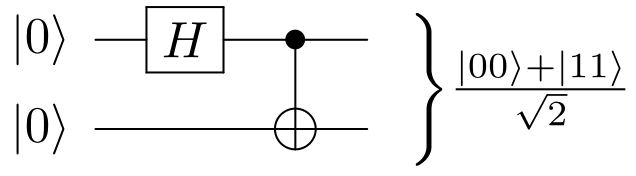
Bell circuit Updated 2025-07-16
qiskit/hello.py Updated 2025-07-16
Sample program output,
counts are randomized each time.First we take the quantum state vector immediately after the input.We understand that the first element of
input:
state:
Statevector([1.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
dims=(2, 2))
probs:
[1. 0. 0. 0.]Statevector is , and has probability of 1.0.Next we take the state after a Hadamard gate on the first qubit:We now understand that the second element of the
h:
state:
Statevector([0.70710678+0.j, 0.70710678+0.j, 0. +0.j,
0. +0.j],
dims=(2, 2))
probs:
[0.5 0.5 0. 0. ]Statevector is , and now we have a 50/50 propabability split for the first bit.Then we apply the CNOT gate:which leaves us with the final .
cx:
state:
Statevector([0.70710678+0.j, 0. +0.j, 0. +0.j,
0.70710678+0.j],
dims=(2, 2))
probs:
[0.5 0. 0. 0.5]Then we print the circuit a bit:
qc without measure:
┌───┐
q_0: ┤ H ├──■──
└───┘┌─┴─┐
q_1: ─────┤ X ├
└───┘
c: 2/══════════
qc with measure:
┌───┐ ┌─┐
q_0: ┤ H ├──■──┤M├───
└───┘┌─┴─┐└╥┘┌─┐
q_1: ─────┤ X ├─╫─┤M├
└───┘ ║ └╥┘
c: 2/═══════════╩══╩═
0 1
qasm:
OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
h q[0];
cx q[0],q[1];
measure q[0] -> c[0];
measure q[1] -> c[1]; Microsoft Updated 2025-07-16
They are evil because they produce closed source offline software used by millions: Microsoft Windows.
And also their monopolistic practices: United States v. Microsoft Corp.
So, as put in Video "Bill Gates vs Steve Jobs by Epic Rap Battles of History (2012)" by fake Steve Jobs to fake Bill Gates:
However, like all big tech companies with infinite money, they do end up doing some cool things in their research department, Microsoft Research, notably for Ciro Santilli being:
- Lean
- their quantum computing work. C is of course a bad idea, we don't need yet another domain-specific language, Python library based solutions like Qiskit are obviously the way to go
OpenQASM Updated 2025-07-16
E.g. with our qiskit/hello.py, we obtain the Bell state circuit:
OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
h q[0];
cx q[0],q[1];
measure q[0] -> c[0];
measure q[1] -> c[1]; qiskit/initialize.py Updated 2025-07-16
In this example we will initialize a quantum circuit with a single CNOT gate and see the output values.
By default, Qiskit initializes every qubit to 0 as shown in the qiskit/hello.py. But we can also initialize to arbitrary values as would be done when computing the output for various different inputs.
Output:which we should all be able to understand intuitively given our understanding of the CNOT gate and quantum state vectors.
┌──────────────────────┐
q_0: ┤0 ├──■──
│ Initialize(1,0,0,0) │┌─┴─┐
q_1: ┤1 ├┤ X ├
└──────────────────────┘└───┘
c: 2/═════════════════════════════
init: [1, 0, 0, 0]
probs: [1. 0. 0. 0.]
init: [0, 1, 0, 0]
probs: [0. 0. 0. 1.]
init: [0, 0, 1, 0]
probs: [0. 0. 1. 0.]
init: [0, 0, 0, 1]
probs: [0. 1. 0. 0.]
┌──────────────────────────────────┐
q_0: ┤0 ├──■──
│ Initialize(0.70711,0,0,0.70711) │┌─┴─┐
q_1: ┤1 ├┤ X ├
└──────────────────────────────────┘└───┘
c: 2/═════════════════════════════════════════
init: [0.7071067811865475, 0, 0, 0.7071067811865475]
probs: [0.5 0.5 0. 0. ]quantumcomputing.stackexchange.com/questions/13202/qiskit-initializing-n-qubits-with-binary-values-0s-and-1s describes how to initialize circuits qubits only with binary 0 or 1 to avoid dealing with the exponential number of elements of the quantum state vector.
Quantum circuits vs classical circuits Updated 2025-07-16
Just like a classic programmer does not need to understand the intricacies of how transistors are implemented and CMOS semiconductors, the quantum programmer does not understand physical intricacies of the underlying physical implementation.
The main difference to keep in mind is that quantum computers cannot save and observe intermediate quantum state, so programming a quantum computer is basically like programming a combinatorial-like circuit with gates that operate on (qu)bits:
For this reason programming a quantum computer is much like programming a classical combinatorial circuit as you would do with SPICE, verilog-or-vhdl, in which you are basically describing a graph of gates that goes from the input to the output
For this reason, we can use the words "program" and "circuit" interchangeably to refer to a quantum program
Also remember that and there is no no clocks in combinatorial circuits because there are no registers to drive; and so there is no analogue of clock in the quantum system either,
Quantum compilation Updated 2025-07-16
Quantum Fourier transform Updated 2025-07-16
Sample implementations: