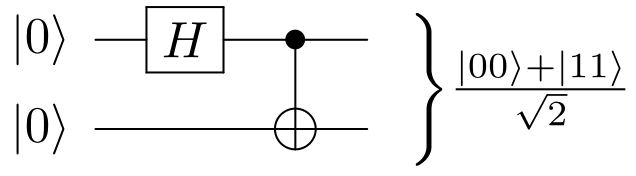
One of the four following states:

∣ Φ^{+} ⟩ = \frac{1}{2} (∣ 00 ⟩ + ∣ 11 ⟩) ∣ Φ^{-} ⟩ = \frac{1}{2} (∣ 00 ⟩ - ∣ 11 ⟩) ∣ Ψ^{+} ⟩ = \frac{1}{2} (∣ 01 ⟩ + ∣ 10 ⟩) ∣ Ψ^{-} ⟩ = \frac{1}{2} (∣ 01 ⟩ - ∣ 10 ⟩)

When unqualified as in "the Bell state", it generally just means

∣ Φ^{+} ⟩

The Bell states are entangled and non-separable. Intuitively, we can see that when we measure that state, the values of the first and second bit are strictly correlated. This is the hallmark of quantum computation: making up states where qubits are highly correlated to match a specific algorithmic answer, and opposed to uniformly random noise. For example, the Bell state circuit is a common hello world, e.g. it is used in the official Qiskit hello world.

Bell circuit

 0  0

A quantum circuit which when fed with input

∣ 00 ⟩

produces the Bell state.

In Qiskit at: qiskit/hello.py.

Figure 1.
Quantum circuit that generates the Bell state
. Source.
The fundamental intuition for this circuit is as follows.
First the Hadamard gate makes the first qubit be in a 50/50 state.
Then, the CNOT gate gets controlled by that 50/50 value, and the controlled qubit also gets 50/50 chance as a result.
However, both qubits are now entangled: the result of the second qubit depends on the result of the first one. Because:
if the first qubit is 0, cnot is not active, and so the second qubit remains 0 as its input
if the first qubit is 1, cnot is active, and so the second qubit is flipped to 1

Greenberger-Horne-Zeilinger state

 2  0

Quantum memory

 1  0

TODO clear example and application.

www.quantamagazine.org/quantum-memory-proves-exponentially-powerful-20241016/ from Quanta Magazine has an incomprehensible news of something that sounds cool

 Ancestors (7)

 Incoming links (3)

 View article source

 Discussion (0)

New discussion

There are no discussions about this article yet.

 Articles by others on the same topic (2)

Quantum state by

Codex  0 Created 2026-09-24 Updated 2026-10-20

 View more

A quantum state describes a preparation through its predicted measurement in quantum mechanics probabilities. In the Hilbert space formulation, a pure state is a quantum state ray: a normalized vector representative

∣ ψ ⟩

satisfies

⟨ ψ ∣ ψ ⟩ = 1

, and representatives differing by a global phase describe the same quantum state. ^[ref]

Both pure states and mixed states are represented by a density operator on the chosen complex Hilbert space:

ρ = ρ^{†}, ⟨ v ∣ ρ ∣ v ⟩ \geq 0 for every ∣ v ⟩, Tr ρ = 1.

(1)

Thus

ρ

is Hermitian, positive semidefinite and of unit trace; in infinite dimension it must also be a trace-class operator. For a normalized pure state,

ρ = ∣ ψ ⟩ ⟨ ψ ∣

is a rank-one orthogonal projection. A mixed state has no single such vector representative. Its density matrix is the matrix of

ρ

in a chosen orthonormal basis. ^[ref] For a discrete POVM with effects

E_{a} \geq 0

and

\sum_{a} E_{a} = I

, the Born rule reads

P (a) = Tr (ρ E_{a}), P (a) = ⟨ ψ ∣ E_{a} ∣ ψ ⟩ for a pure state .

(2)

These constraints and Born rule probabilities describe arbitrary finite-dimensional preparations. ^[ref]

Randomly choosing normalized pure states with probabilities

w_{j}

and forgetting the label gives

ρ = \sum_{j} w_{j} ∣ ψ_{j} ⟩ ⟨ ψ_{j} ∣, w_{j} \geq 0, \sum_{j} w_{j} = 1.

(3)

This quantum state ensemble averages probabilities; a quantum superposition adds probability amplitudes. Several ensembles can give the same density operator. Quantum entanglement can make a reduced density matrix mixed while the joint quantum state is pure. ^[ref]

The preparation, the choice of basis, and the measurement are separate ingredients. A wavefunction

ψ (x) = ⟨ x ∣ ψ ⟩

is the position representation of a pure state; a general mixed state requires a density operator. For a closed quantum system, a unitary operator evolves it as

ρ \mapsto U ρ U^{†}

, preserving its eigenvalues and purity of a density operator. ^[ref] The Bloch sphere and Bloch ball give the qubit geometry; quantum state tomography connects repeated preparations to an estimated density matrix; projective measurement treats the conditional state after an outcome.

 Read the full article

Quantum state by

Wikipedia Bot  1

 View more

A quantum state is a fundamental concept in quantum mechanics that describes the state of a quantum system. It encapsulates all the information about the system and can be represented in several ways, such as: 1. **Wave Function**: In non-relativistic quantum mechanics, a quantum state can be represented by a wave function, usually denoted by the Greek letter psi (Ψ).

 Read the full article

  See all articles in the same topic Create my own version

 Discussion (0)  Subscribe (1)

 Discussion (0)