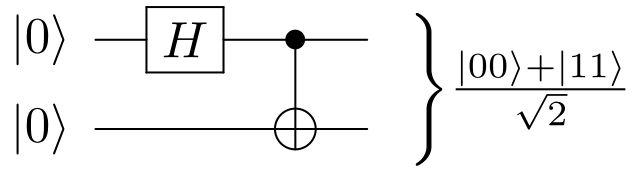
Bell circuit Updated 2025-07-16
CNOT gate Updated 2025-07-16
The CNOT gate is a controlled quantum gate that operates on two qubits, flipping the second (operand) qubit if the first (control) qubit is set.
Equation 1.
CNOT gate matrix
. CNOT gate symbol
. Source. The symbol follow the generic symbol convention for controlled quantum gates shown at Figure "Generic controlled quantum gate symbol", but replacing the generic "U" with the Figure "Quantum NOT gate symbol".On the standard basis:we see that this means that only and should be possible. Therefore, the state must be of the form:where and are two complex numbers such that
If we operate the CNOT gate on that state, we obtain:and so the input is unchanged as desired, because the control qubit is 0.
Therefore, in that case, what happened is that the probabilities of and were swapped from and to and respectively, which is exactly what the quantum NOT gate does.
So from this we understand more concretely what "the gate only operates if the first qubit is set to one" means.
Now go and study the Bell state and understand intuitively how this gate is used to produce it.
Introduction to quantum computing Updated 2025-08-08
Course plan:
- Section "Programmer's model of quantum computers"
- look at a Qiskit hello world
- e.g. ours: qiskit/hello.py
- learn about quantum circuits.
- tensor product in quantum computing
- First we learn some quantum logic gates. This shows an alternative, and extremely important view of a quantum computer besides a matrix multiplication: as a circuit. Fundamental subsections:
- quantum algorithms
Tensor product in quantum computing Updated 2025-07-16
We don't need to understand a super generalized version of tensor products to know what they mean in basic quantum computing!
Intuitively, taking a tensor product of two qubits simply means putting them together on the same quantum system/computer.
The quantum state is called a separable state, because it can be written as a single product of two different qubits. We have simply brought two qubits together, without making them interact.
If we then add a CNOT gate to make a Bell state:we can now see that the Bell state is non-separable: we've made the two qubits interact, and there is no way to write this state with a single tensor product. The qubits are fundamentally entangled.