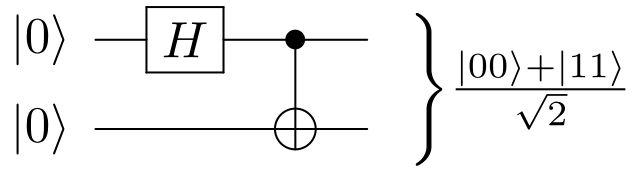
Bell circuit Updated 2025-05-26 +Created 1970-01-01
View more
A quantum circuit which when fed with input produces the Bell state.
Figure 1.
Quantum circuit that generates the Bell state
. Source.
The fundamental intuition for this circuit is as follows.
First the Hadamard gate makes the first qubit be in a 50/50 state.
Then, the CNOT gate gets controlled by that 50/50 value, and the controlled qubit also gets 50/50 chance as a result.
However, both qubits are now entangled: the result of the second qubit depends on the result of the first one. Because:
Read the full article
qiskit/hello.py Updated 2025-05-26 +Created 1970-01-01
View more
Our example uses a Bell state circuit to illustrate all the fundamental Qiskit basics.
Sample program output, counts are randomized each time.
First we take the quantum state vector immediately after the input.
input:
state:
Statevector([1.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
            dims=(2, 2))
probs:
[1. 0. 0. 0.]
We understand that the first element of Statevector is , and has probability of 1.0.
Next we take the state after a Hadamard gate on the first qubit:
h:
state:
Statevector([0.70710678+0.j, 0.70710678+0.j, 0.        +0.j,
             0.        +0.j],
            dims=(2, 2))
probs:
[0.5 0.5 0.  0. ]
We now understand that the second element of the Statevector is , and now we have a 50/50 propabability split for the first bit.
Then we apply the CNOT gate:
cx:
state:
Statevector([0.70710678+0.j, 0.        +0.j, 0.        +0.j,
             0.70710678+0.j],
            dims=(2, 2))
probs:
[0.5 0.  0.  0.5]
which leaves us with the final .
Then we print the circuit a bit:
qc without measure:
     ┌───┐
q_0: ┤ H ├──■──
     └───┘┌─┴─┐
q_1: ─────┤ X ├
          └───┘
c: 2/══════════

qc with measure:
     ┌───┐     ┌─┐
q_0: ┤ H ├──■──┤M├───
     └───┘┌─┴─┐└╥┘┌─┐
q_1: ─────┤ X ├─╫─┤M├
          └───┘ ║ └╥┘
c: 2/═══════════╩══╩═
                0  1
qasm:
OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
h q[0];
cx q[0],q[1];
measure q[0] -> c[0];
measure q[1] -> c[1];
And finally we compile the circuit and do some sample measurements:
qct:
     ┌───┐     ┌─┐
q_0: ┤ H ├──■──┤M├───
     └───┘┌─┴─┐└╥┘┌─┐
q_1: ─────┤ X ├─╫─┤M├
          └───┘ ║ └╥┘
c: 2/═══════════╩══╩═
                0  1
counts={'11': 484, '00': 516}
counts={'11': 493, '00': 507}
Read the full article
Hadamard gate Updated 2025-05-26 +Created 1970-01-01
View more
The Hadamard gate takes or (quantum states with probability 1.0 of measuring either 0 or 1), and produces states that have equal probability of 0 or 1.
(1)
Equation 1.
Hadamard gate matrix
.
Figure 1.
Hadamard gate symbol
. Source.
Read the full article
Introduction to quantum computing Updated 2025-05-26 +Created 1970-01-01
View more
Read the full article
Single-qubit gate Updated 2025-05-26 +Created 1970-01-01
View more
The first two that you should study are:
Read the full article
Tensor product in quantum computing Updated 2025-05-26 +Created 1970-01-01
View more
We don't need to understand a super generalized version of tensor products to know what they mean in basic quantum computing!
Intuitively, taking a tensor product of two qubits simply means putting them together on the same quantum system/computer.
When we write the bra-ket notation: that is the same as .
The tensor product is called a "product" because it distributes over addition.
E.g. consider:
(1)
Intuitively, in this operation we just put a Hadamard gate qubit together with a second pure qubit.
And the outcome still has the second qubit as always 0, because we haven't made them interact.
The quantum state is called a separable state, because it can be written as a single product of two different qubits. We have simply brought two qubits together, without making them interact.
If we then add a CNOT gate to make a Bell state:
(2)
we can now see that the Bell state is non-separable: we've made the two qubits interact, and there is no way to write this state with a single tensor product. The qubits are fundamentally entangled.
Read the full article