2017. Directed by Michael Oswald. Adam Curtis vibes.
Some notable points:
- the role of the British Overseas Territories as tax havens
- the role of the City of London in setting economic policy
- the role of trusts
Bibliography:
Some mechanics:
- inter agent communication
- compute power is limited by limiting Java bytecode count execution per bot per cycle
Battlecode Final Tournament 2023
. Source. Introduction to Battlecode by MIT OpenCourseWare (2014)
Source. The Quora question: www.quora.com/Are-there-any-PhD-programs-in-training-an-AI-system-to-play-computer-games-Like-the-work-DeepMind-do-combining-Reinforcement-Learning-with-Deep-Learning-so-the-AI-can-play-Atari-games
- stackoverflow.com/questions/600079/how-do-i-clone-a-subdirectory-only-of-a-git-repository/52269934#52269934
- summaries:
- dupes:
- file or directory
- file
- only small files:
For the strong.
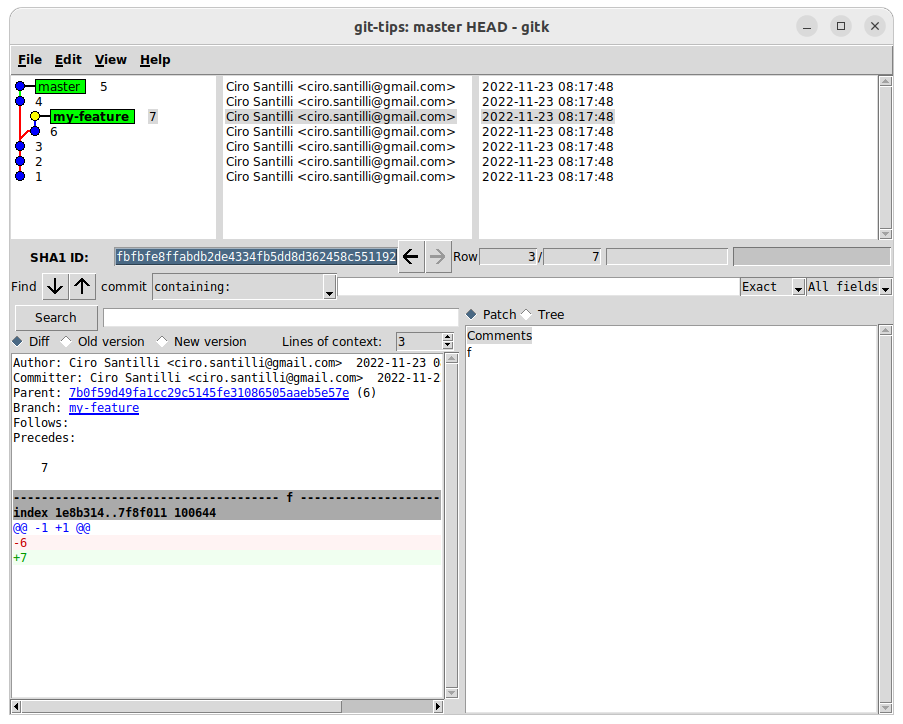
git log --abbrev-commit --decorate --graph --pretty=oneline master HEADOutput:
* b4ec057 (master) 5
* 0b37c1b 4
| * fbfbfe8 (HEAD -> my-feature) 7
| * 7b0f59d 6
|/
* 661cfab 3
* 6d748a9 2
* c5f8a2c 1If we also add the As we can see, this removes any commit that is neither:
--simplify-by-decoration, which you very often want want on a real repository with many commits:* b4ec057 (master) 5
| * fbfbfe8 (HEAD -> my-feature) 7
|/
* c5f8a2c 1- under a branch or tag
- at the intersection of too branches or tags
In order to solve conflicts, you just have to understand what commit you are trying to move where.
E.g. if from:we do:what happens step by step is first 6 is moved on top of 5:and then 7 is moved on top of the new 6:
5 master
|
4 7 my-feature HEAD
| |
3 6
|/
2
|
1git rebase master6on5 HEAD
|
5 master
|
4 7 my-feature
| |
3 6
| |
2-----------------+
|
17on5 HEAD
|
6on5
|
5 master
|
4 7 my-feature
| |
3 6
| |
2-----------------+
|
17on5 my-feature HEAD
|
6on5
|
5 master
|
4
|
3
|
2
|
1 Git tips The key to solve conflicts: see the two conflicting diffs by  Ciro Santilli 37 Updated 2025-07-16
Ciro Santilli 37 Updated 2025-07-16
The key to solve conflicts is:
You have to understand what are the two commits that touched a given line (one from master, one from features), and then combine them somehow.
CLI hello world:
gnuplot -p -e 'p sin(x)' Unlisted articles are being shown, click here to show only listed articles.