Ciro Santilli @cirosantilli 35

 Incoming links: Spacelike-separated event

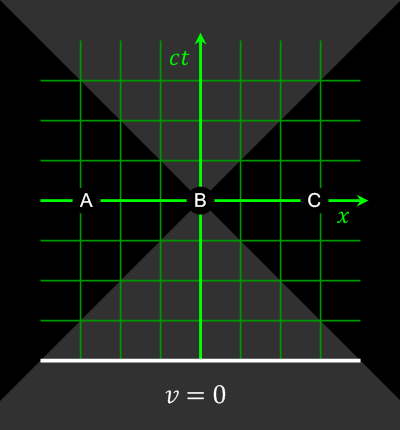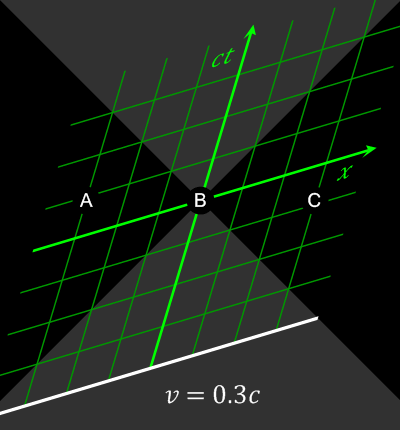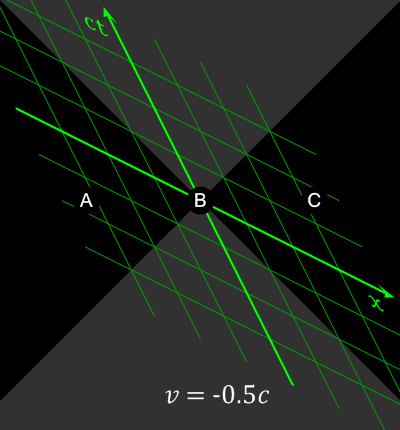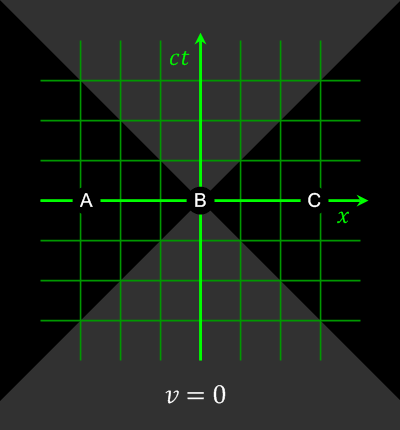
Length contraction  Updated 2025-01-10  +Created 1970-01-01

Suppose that a rod has is length

L

measured on a rest frame

S

(or maybe even better: two identical rulers were manufactured, and one is taken on a spaceship, a bit like the twin paradox).

Question: what is the length

L^{'}

than an observer in frame

S^{'}

moving relative to

S

as speed

v

observe the rod to be?

The key idea is that there are two events to consider in each frame, which we call 1 and 2:

the left end of the rod is an observation event at a given position at a given time: $x_{1}$ and $t_{1}$ for $S$ or $x_{1}^{'}$ and $t_{1}^{'}$ for $S^{'}$
the right end of the rod is an observation event at a given position at a given time : $x_{2}$ and $t_{2}$ for $S$ or $x_{2}^{'}$ and $t_{2}^{'}$ for $S^{'}$

Note that what you visually observe on a photograph is a different measurement to the more precise/easy to calculate two event measurement. On a photograph, it seems you might not even see the contraction in some cases as mentioned at en.wikipedia.org/wiki/Terrell_rotation

Measuring a length means to measure the

x_{2} - x_{1}

difference for a single point in time in your frame (

t 2 = t 1

So what we want to obtain is

x_{2}^{'} - x_{1}^{'}

for any given time

t^{'} 2 = t^{'} 1

In summary, we have:

L L^{'} = x_{2} = x_{2}^{'} - x_{1} - x_{1}^{'} t_{2}^{'} = t_{1}^{'}

(1)

By plugging those values into the Lorentz transformation, we can eliminate

t_{2} a n d t_{1}

, and conclude that for any

t_{2}^{'} = t_{1}^{'}

, the length contraction relation holds:

L^{'} = \frac{L}{γ}

(2)

The key question that needs intuitive clarification then is: but how can this be symmetric? How can both observers see each other's rulers shrink?

And the key answer is: because to the second observer, the measurements made by the first observer are not simultaneous. Notably, the two measurement events are obviously spacelike-separated events by looking at the light cone, and therefore can be measured even in different orders by different observers.

 Read the full article

Light cone  Updated 2025-01-10  +Created 1970-01-01

 View more

A subset of Spacetime diagram.

The key insights that it gives are:

future and past are well defined: every reference frame sees your future in your future cone, and your past in your past cone
Otherwise causality could be violated, and then things would go really bad, you could tell your past self to tell your past self to tell your past self to do something.
You can only affect the outcome of events in your future cone, and you can only be affected by events in your past cone. You can't travel fast enough to affect.
Two spacetime events with such fixed causality are called timelike-separated events.
every other event (to right and left, known as spacelike-separated events) can be measured to happen before or after your current spacetime event by different observers.
But that does not violate causality, because you just can't reach those spacetime points anyways to affect them.

Figure 1.
Animation showing how space-separated events can be observed to happen in different orders by observers in different frames of reference
. Source.

 Read the full article

Timelike-separated event  Updated 2025-01-10  +Created 1970-01-01

 View more

The opposite of spacelike-separated events.

 Read the full article

Transversal time dilation  Updated 2025-01-10  +Created 1970-01-01

 View more

Light watch transverse to direction of motion. This case is interesting because it separates length contraction from time dilation completely.

Of course, as usual in special relativity, calling something "time dilation" leads us to mind boggling ideas of "symmetry breaking": if both frames have a light watch, how can both possibly observe the other to be time dilated?

And the answer to this, is the usual: in special relativity time and space are interwoven in a fucked up way, everything is just a spacetime event.

In this case, there are three spacetime events of interest: both clocks start at same position, your beam hits up at x=0, moving frame hits up at x>0.

Those two mentioned events are spacelike-separated events, and therefore even though they seem simultaneous to you, they are not going to be simultaneous to the moving observer!

If little clock one meter away from you tells you that at the time of some event (your light beam hit up) the moving light watch was only 50% up, this is just a number given by your one meter away watch!

 Read the full article