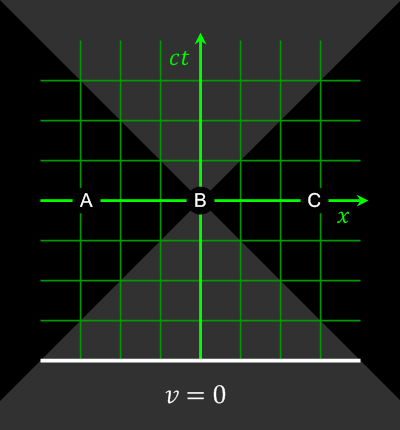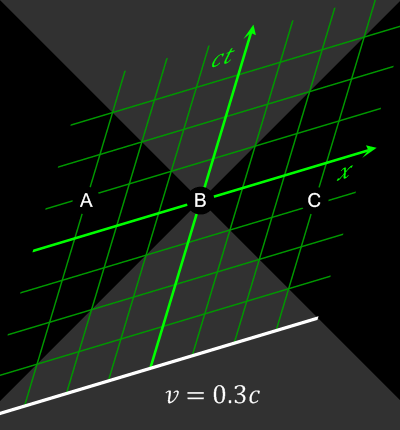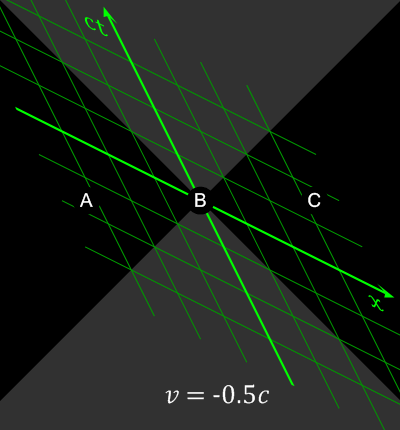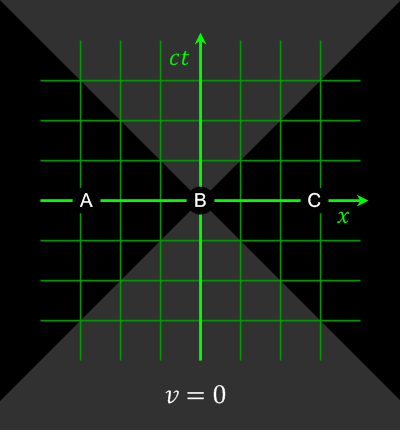
Explains how it is possible that everyone observes the same speed of light, even if they are moving towards or opposite to the light!!!
This was first best observed by the Michelson-Morley experiment, which uses the movement of the Earth at different times of the year to try and detect differences in the speed of light.
This leads leads to the following conclusions:
- to length contraction and time dilation
- the speed of light is the maximum speed anything can reach
The "special" in the name refers to the fact that it is a superset of general relativity, which also explains gravity in a single framework.
Since time and space get all messed up together, you have to be very careful to understand what it means to say "I observed this to happen over there at that time", otherwise you will go crazy. A good way to think about is this:
- use Einstein synchronization to setup a bunch of clocks for every position in your frame of reference
- on every point of space, you put a little detector which records events and the time of the event
- each detector can only detect events locally, i.e. events that happen very close to the detector
- then, after the event, the detectors can send a signal to you, who is sitting at the origin, telling you what they detected
This single experimental observation/idea is the basis for all of special relativity.
Special relativity is the direct result of people bending their backs to accommodate for this really weird fact.
Bibliography:
- Subtle is the Lord by Abraham Pais (1982) chapter III "Relativity, the special theory" has a good sketch as you may imagine.
Can you just imagine what if luminiferous aether was one single fixed rigid body? This is apparently what Maxwell believed, Subtle is the Lord by Abraham Pais (1982) page 111 quoting his entry to Encyclopedia Britannica:Then it would provide a natural space coordinate for the entire universe!
There can be no doubt that the interplanetary and interstellar spaces are not empty but are occupied by a material substance or body, which is certainly the largest, and probably the most uniform, body of which we have any knowledge.
Apparently Einstein was the first to completely say: let's just screw this aether thing completely then, it's getting too complicated, and we don't really need it. As Wikipedia puts it well, in very unencyclopedic tone[ref]: Aether fell to Occam's razor.
Given experiments such as the Fizeau experiment and the Michelson-Morley experiment that couldn't really detect the Earth's movement across aether, people started to wonder if the Earth wasn't dragging the luminiferous aether.
- moving magnet and conductor problem: the more experiments confirm Maxwell's equations, the more special relativity has to be correct
- aberration TODO more precisely how it is evidence.
Michelson Interferometer by Amrita Vlab (2013)
Source. Shows the optical controls and alignment in more detail.Michelson Interferometer by TSG Physics (2012)
Source. TSG PHysiQuantum electrodynamics bibliographycs is the channel from the MIT Department of Physics Technical Services Group. In the video they produce a very clear round interference pattern.This paper is in the public domain and people have uploaded it e.g. to glorious Wikisource: en.wikisource.org/wiki/On_the_Relative_Motion_of_the_Earth_and_the_Luminiferous_Ether including its amazing illustrations.
Fig 3 from On the Relative Motion of the Earth and the Luminiferous Ether
. Source. Amazing 3D technical drawing from the 19th century!!!The equation that allows us to calculate stuff in special relativity!
Take two observers with identical rules and stopwatch, and aligned axes, but one is on a car moving at towards the direction at speed .
When both observe an event, if we denote:It is of course arbitrary who is standing and who is moving, we will just use the term "standing" for the one without primes.
- the observation of the standing observer
- the observation of the ending observer on a car
Note that if tends towards zero, then this reduces to the usual Galilean transformations which our intuition expects:
This explains why we don't observe special relativity in our daily lives: macroscopic objects move too slowly compared to light, and is almost zero.
Same motivation as Galilean invariance, but relativistic version of that: we want the laws of physics to have the same form on all inertial frames, so we really want to write them in a way that is Lorentz covariant.
This is just the relativistic version of that which takes the Lorentz transformation into account instead of just the old Galilean transformation.
OK, so let's verify the main desired consequence of the Lorentz transformation: that everyone observes the same speed of light.
Observers will measure the speed of light by calculating how long it takes the light going towards cross a rod of length laid in the x axis at position .
Each observer will observe two events:
Supposing that the standing observer measures the speed of light as and that light hits the left side of the rod at time , then he observes the coordinates:
Now, if we transform for the moving observer:and so the moving observer measures the speed of light as:
Suppose that a rod has is length measured on a rest frame (or maybe even better: two identical rulers were manufactured, and one is taken on a spaceship, a bit like the twin paradox).
Question: what is the length than an observer in frame moving relative to as speed observe the rod to be?
The key idea is that there are two events to consider in each frame, which we call 1 and 2:Note that what you visually observe on a photograph is a different measurement to the more precise/easy to calculate two event measurement. On a photograph, it seems you might not even see the contraction in some cases as mentioned at en.wikipedia.org/wiki/Terrell_rotation
- the left end of the rod is an observation event at a given position at a given time: and for or and for
- the right end of the rod is an observation event at a given position at a given time : and for or and for
By plugging those values into the Lorentz transformation, we can eliminate , and conclude that for any , the length contraction relation holds:
The key question that needs intuitive clarification then is: but how can this be symmetric? How can both observers see each other's rulers shrink?
And the key answer is: because to the second observer, the measurements made by the first observer are not simultaneous. Notably, the two measurement events are obviously spacelike-separated events by looking at the light cone, and therefore can be measured even in different orders by different observers.
What you would see the moving rod look like on a photo of a length contraction experiment, as opposed as using two locally measured separate spacetime events to measure its length.
One of the best ways to think about it is the transversal time dilation thought experiment.
Light watch transverse to direction of motion. This case is interesting because it separates length contraction from time dilation completely.
Of course, as usual in special relativity, calling something "time dilation" leads us to mind boggling ideas of "symmetry breaking": if both frames have a light watch, how can both possibly observe the other to be time dilated?
And the answer to this, is the usual: in special relativity time and space are interwoven in a fucked up way, everything is just a spacetime event.
In this case, there are three spacetime events of interest: both clocks start at same position, your beam hits up at x=0, moving frame hits up at x>0.
Those two mentioned events are spacelike-separated events, and therefore even though they seem simultaneous to you, they are not going to be simultaneous to the moving observer!
If little clock one meter away from you tells you that at the time of some event (your light beam hit up) the moving light watch was only 50% up, this is just a number given by your one meter away watch!
The key question is: why is this not symmetrical?
One answer is: because one of the twin accelerates, and therefore changes inertial frames.
But the better answer is: understand what happens when the stationary twin sends light signals at constant time intervals to each other. When does the travelling twin receives them?
Another way of understanding it is: you have to make all calculations on a single inertial frame for the entire trip.
Supposing the sibling quickly accelerates out (or magically starts moving at constant speed), travels at constant speed, and quickly accelerates back, and travels at constant speed setup, there are three frames that seem reasonable:
- the frame of the non-accelerating sibling
- the outgoing trip of the accelerating sibling
- the return trip of the accelerating sibling
If you do that, all three calculations give the exact same result, which is reassuring.
Another way to understand it is to do explicit integrations of the acceleration: physics.stackexchange.com/questions/242043/what-is-the-proper-way-to-explain-the-twin-paradox/242044#242044 This is the least insightful however :-)
Bibliography:
The following aspects of Maxwell's equations make no sense without special relativity:
- the Lorentz force would be different observers have different speeds, see e.g.: charged particle moving at the same speed of electrons thought experiment
- Maxwell's equations imply that the speed of light is the same for all inertial reference frames
When charged particle though experiment are seen from the point of view of special relativity, it becomes clear that magnetism is just a direct side effect of charges being viewed in special relativity. One is philosophically reminded of how spin is the consequence of quantum mechanics + special relativity.
Bibliography:
It appears that Maxwell's equations can be derived directly from Coulomb's law + special relativity:
This idea is suggested by the charged particle moving at the same speed of electrons thought experiment, which indicates that magnetism is just a consenquence of special relativity.
Why moving charges produce magnetic field? by FloatHeadPhysics (2022)
Source. In the above experiment:
- from the wire frame, the charge feels electromagnetic force, because it is moving and there is a magnetic field
- from the single charge frame, there is still magnetic field (positive charges are moving), but the body itself is not moving, so there is no force!
The solution to this problem is length contraction: the positive charges are length contracted and the moving electrons aren't, and therefore they are denser and therefore there is an effective charge from that frame.
This is also mentioned at David Tong www.damtp.cam.ac.uk/user/tong/em/el4.pdf (archive) "David Tong: Lectures on Electromagnetism - 5. Electromagnetism and Relativity" "5.2.1 Magnetism and Relativity".
How Special Relativity Fixed Electromagnetism by The Science Asylum (2019)
Source. See also: covariance.
Subtle is the Lord by Abraham Pais (1982) chapter III "Relativity, the special theory" mentions that this fact and its importance (we want the laws of physics to look the same on all inertial frames, AKA Lorentz covariance) was first fully relized by poincaré in 1905.
And at that same time poincaré also immediately started to think about the other fundamental force then known: gravity, and off the bat realized that gravitational waves must exist. general relativities is probably just "the simplest way to make gravity Lorentz covariant".
Bibliography:
- www.youtube.com/watch?v=nrBiDRZRK5g Maxwell Lagrangian Derivation by Dietterich Labs (2019)
- www.youtube.com/watch?v=yo-Z3RO-eeY Deriving the Maxwell Lagrangian by Pretty Much Physics (2019)
A 4D gradient with some small special relativity specifics added in (the light of speed and sign change for the time).
Because the Minkowski inner product product is not positive definite, the norm induced by an inner product is a norm, and the space is not a metric space strictly speaking.
This form is not really an inner product in the common modern definition, because it is not positive definite, only a symmetric bilinear form.
By default, we will use the time negative representation unless stated otherwise:but another equivalent one is to use a time positive representation:The matrix is typically denoted by the Greek letter eta.
Answer: it can give some qualitative intuition on what is larger/smaller happens before/after based only on arguably more intuitive geometric considerations, without requiring you to do any calculations, see e.g. Figure "Spacetime diagram illustrating how faster-than-light travel implies time travel".
The key insights that it gives are:
- future and past are well defined: every reference frame sees your future in your future cone, and your past in your past coneOtherwise causality could be violated, and then things would go really bad, you could tell your past self to tell your past self to tell your past self to do something.
- every other event (to right and left, known as spacelike-separated events) can be measured to happen before or after your current spacetime event by different observers.
Animation showing how space-separated events can be observed to happen in different orders by observers in different frames of reference
. Source. The opposite of spacelike-separated events.
Mathematically, we can decide if two events are timelike-separated or spacelike-separated by just looking at the sign of the spacetime interval between them.
On the light cone, these are events on the left/right part of the cone.
Different observers might not agree on the order of two spacelike-separated events.
Further discussion at Section "Light cone".
The opposite of those events are timelike-separated events.
In the Galilean transformation, there are two separate invariants that two inertial frame of reference always agree on between two separate events:
- time
- length, given by the Pythagorean theorem
However, in special relativity, neither of those are invariant separately, since space and time are mixed up together.
Note that this distance can be zero for two events separated.
Articles by others on the same topic
This is a section about Special relativity!
For example, this sentence. And then another one.
Special relativity is a fundamental theory in physics developed by Albert Einstein and introduced in his 1905 paper "On the Electrodynamics of Moving Bodies." The theory revolutionized our understanding of space, time, and motion, and it is based on two primary postulates: 1. **The Principle of Relativity**: The laws of physics are the same in all inertial frames of reference, meaning that the laws apply equally for observers in uniform motion relative to one another.
This is a section about Special relativity!
For example, this sentence. And then another one.