Sponsor Ciro Santilli's work on OurBigBook.com Progress updates Updated 2025-11-21
Education is broken Updated 2025-11-21
Once Ciro was at a University course practical session, and a graduate was around helping out. Ciro asked if what the graduate did anything specifically related to the course, and they replied they didn't. And they added that:Even though Ciro was already completely disillusioned by then, that still made an impression on him. Something is really wrong with this shit.
One has to put the bread on the table.
Other people that think that the educational system is currently bullshit as of 2020:
- Einstein, quoted in The New York Times, March 13 1949, p. 34:[ref]
- Ron Maimon
- Xavier Niel: fortune.com/2018/11/30/billionaire-xavier-niel/ "Want This Billionaire's Attention? Drop Out of School" (2018). He also created 42.
- Year On
- by Zach Caceres
- Anand Raja submission "Students and Universities": publications.parliament.uk/pa/cm200809/cmselect/cmdius/170/170ii.pdf, www.linkedin.com/in/anandraja/.
- xsrus.com/life-school-and-the-80-20-rule. Also GPA 2.0 linked from xsrus.com/ to xsrus.com/gpa-2.0 but down now
- A Mathematician's Lament by Paul Lockhart www.maa.org/external_archive/devlin/LockhartsLament.pdf
- www.learningforreal.org/quotes/ quotes Elbert Hubbard:She's somewhat focused on the performing arts, but what she says applies basically equally well to the natural sciences. A talk: www.youtube.com/watch?v=ggYL9gQeVEk She talks about authentic learning.
- www.youtube.com/watch?v=iG9CE55wbtY Do schools kill creativity? by Sir Ken Robinson (2017)
- Erik Finman thinks school is broken
- sociable.co/technology/silicon-valley-education-students-entrepreneurs/ Bringing Silicon Valley into Schools: How to Make Students Entrepreneurs of Their Own Education (2016)
- hackeducation.com/2015/04/25/factory-model The Invented History of 'The Factory Model of Education' by Audrey Watters (2015)
- www.forbes.com/councils/forbescoachescouncil/2025/04/17/the-ai-fear-factor-why-leaders-resist-and-how-to-move-forward/ The Single Best Idea for Reforming K-12 Education by Steve Denning (2011)
The problem with education by Ciro Santilli
. Source. In this video Ciro Santilli exposes his fundamental philosophy regarding why Education is broken. This philosophy was the key motivation behind the failed OurBigBook Project.Educational systems are carried by Indian YouTubers meme
. Source. Over a Dmitriy Khaladzhi carrying a horse over his shoulders meme template.Peter Gregory from Silicon Valley shows his hate for university in a fake TED talk
. Source. Key moment: someone from the crowd cries:to which the speaker replies:The true value of snake oil is intangible as well.
David Deutsch on Education interviewed by Aidan McCullen (2019)
Source. Key quote that hits the nail:
So right... the purpose of education is not to teach facts. The purpose of education is to propose ways of thinking, which students themselves must try to apply and decide if it suits them! And use the patterns of thinking that are useful to reach their goals.
Like Noam Chomsky, he proposes education has been a system of indoctrination more than anything else e.g. twitter.com/daviddeutschoxf/status/1406374921748496386:At twitter.com/DavidDeutschOxf/status/1051475227476185089 another good quote by Churchill:
All compulsory education, "tough" or not, "love" or not, in camps or not, and whether it "traumatises" or not, is a violation of human rights.
Headmasters have powers at their disposal with which Prime Ministers have never yet been invested.
Quote selection by Charles Bukowski (2016)
Source. Generally speaking, you're free until you're about 4 years old. Then you go to grammar school and then you start becoming... oriented and shoved into areas. You lose what individualism you have, if you have enough of course, you retain some of it... Then you work the 8 hour job with almost a feeling of goodness, like you're doing something. Then you get married like marriage is a victory, and you have children like children is a victory... Marriage, birth, children. It's something they have to do because there's nothing else to do. There's no glory in it, there's no steam, there's no fire. It's very, very flat... You get caught into the stricture of what you're supposed to be and you have no other choice. You're finally molded and melded into what you're supposed to be. I didn't like this.
Home Updated 2025-12-02
Check out: OurBigBook.com, the best way to publish your scientific knowledge. It's an open source note taking system that can publish from lightweight markup files in your computer both to a multi-user mind melding dynamic website, or as a static website. It's like Wikipedia + GitHub + Stack Overflow + Obsidian mashed up. Source code: github.com/ourbigbook/ourbigbook.
Sponsor me to work on this project. For 400k USD I will quit my job or not get a new job and work on OurBigBook full time for a second year to try and kickstart The Higher Education Revolution. Status: ~44k / 400k USD. At 4M USD I retire/tenure and work on open STEM forever. How to donate: Section "Sponsor Ciro Santilli's work on OurBigBook.com".
I first quit my job 1st June 2024 to work on the project for 1 year after I reached my initial 100k goal mostly via a 1000 Monero donation. For a second follow up year, I increased my requirement to 400k USD to give me more peace of mind as I'm destroying my career in the process. A second year greatly improve chances of success: on year one I improved my tech, on year two I want to come guns blazing to solve courses and get users.
Mission: to live in a world where you can learn university-level mathematics, physics, chemistry, biology and engineering from perfect free open source books that anyone can write to get famous. More rationale: Section "OurBigBook.com"
Explaining things is my superpower, e.g. I was top user #39 on Stack Overflow in 2023[ref][ref] and I have a few 1k+ star educational GitHub repositories[ref][ref][ref][ref]. Now I want to bring that level of awesomeness to masters level Mathematics and Physics. But I can't do it alone! So I created OurBigBook.com to allow everyone to work together towards the perfect book of everything.
My life's goal is to bring hardcore university-level STEM open educational content to all ages. Sponsor me at github.com/sponsors/cirosantilli starting from 1$/month so I can work full time on it. Further information: Section "Sponsor Ciro Santilli's work on OurBigBook.com". Achieving what I call "free gifted education" is my Nirvana.
This website is written in OurBigBook Markup, and it is published on both cirosantilli.com (static website) and outbigbook.om/cirosantilli (multi-user OurBigBook Web instance). Its source code is located at: github.com/cirosantilli/cirosantilli.github.io and also at
cirosantilli.com/_dir and it is licensed under CC BY-SA 4.0 unless otherwise noted.To contact Ciro, see: Section "How to contact Ciro Santilli". He likes to talk with random people of the Internet.
GitHub | Stack Overflow | LinkedIn | YouTube | Twitter | Wikipedia | Zhihu 知乎 | Weibo 微博 | Other accounts
Besides that, I'm also a freedom of speech slacktivist and recreational cyclist. I like Chinese traditional music and classic Brazilian pop. Opinions are my own, but they could be yours too. Tax the rich.
Let's create an educational system with:
- no distinction between university and high school, students just go as fast as they can to what they really want without stupid university entry exams
- fully open source learning material
- on-demand examinations that anyone can easily take without prerequisites
- granular entry selection only for space in specific laboratories or participation in specific novel research projects
I offer:
- online private tutoring for:
- any STEM university course
- passionate younger STEM students (any age) who want to learn university level material and beyond. Can your kid be the next Fields Medalist or Nobel Prize winner? I'm here to help, especially if you are filthy rich! I focus moving students forward as fast as they want on and on producing useful novel tutorials and results
Let your child be my Emile, and me be their Adolfo Amidei, and let's see how far they can go! I will help take your child:and achieve their ambitious STEM goals!- into the best universities
- into the best PhD programs
- educational consulting for institutions looking to improve their STEM courses
- do you know that course or teacher that consistently gets bad reviews every year? I'll work with the teacher to turn the problem around!
- are you looking to create a consistent open educational resources offering to increase your institutions internationally visibility? I can help with that too.
My approach is to:For minors, parents are welcome to join video calls, and all interactions with the student will be recorded and made available to parents.
- propose interesting research projects. The starting point is always deciding the end goal: Section "Backward design"
- learn what is needed to do the project together with the student(s)
- publish any novel results or tutorials/tools produced freely licensed online, and encourage the student to do the same (Section "Let students learn by teaching", digital garden)
I have a proven track of explaining complex concepts in an interesting and useful way. I work for the learner. Teaching statement at: Section "How to teach". Pricing to be discussed. Contact details at: Section "How to contact Ciro Santilli".
I am particularly excited about pointing people to the potential next big things, my top picks these days are:I am also generally interested in:
- quantum computing
- AGI research, in particular AI code generation, automated theorem proving and robotics
- assorted molecular biology technologies
- 20th century physics, notably AMO and condensed matter
- the history of science, and in particular trying to look at seminal papers of a field
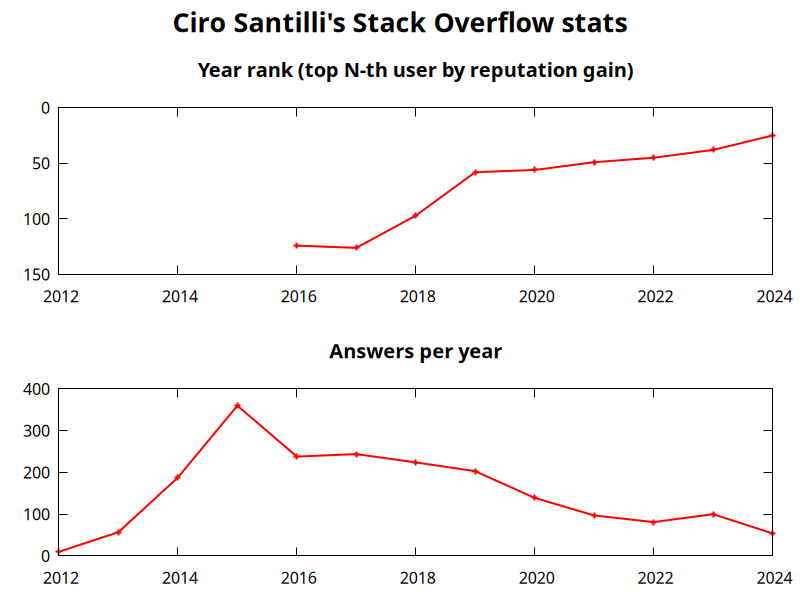
Ciro Santilli's amazing Stack Overflow profile
. Ciro contributes almost exclusively by answering question he Googles into out of his own need, and never by refreshing the newest question of big tags for low hanging fruit! More information at: Section "Ciro Santilli's Stack Overflow contributions".Ciro Santilli's Stack Overflow stats
. Further methodology details at: Figure "Ciro Santilli's Stack Overflow stats".The problem with education by Ciro Santilli
. Source. In this video Ciro Santilli exposes his fundamental philosophy regarding why Education is broken. This philosophy was the key motivation behind the failed OurBigBook Project.OurBigBook Web topics demo
. Source. The OurBigBook topic feature allows users to "merge their minds" in a "sort by upvote"-stack overflow-like manner for each subject. This is the killer feature of OurBigBook Web. More information at: docs.ourbigbook.com/ourbigbook-web-topics.OurBigBook dynamic article tree demo
. Source. The OurBigBook dynamic tree feature allows any of your headers to be the toplevel h1 header of a page, while still displaying its descendants. SEO loves this, and it also allows users to always get their content on the correct granularity. More information at: docs.ourbigbook.com/ourbigbook-web-dynamic-article-tree.OurBigBook local editing and publishing demo
. Source. With OurBigBook you can store your content as plaintext files in a Lightweight markup, and then publish that to either OurBigBook.com to get awesome multi-user features, or as a static website where you are in full control. More information at: docs.ourbigbook.com/publish-your-content.Top Down 2D continuous game with Urho3D C++ SDL and Box2D for Reinforcement learning by Ciro Santilli (2018)
Source. More information: Section "Ciro's 2D reinforcement learning games". This is Ciro's underwhelming stab at the fundamental question: Can AGI be trained in simulations?. This project could be taken much further.Water Margin tribute to Chinese dissidents by Ciro Santilli (2022)
Source. Part of Ciro Santilli's campaign for freedom of speech in China, see also: cirosantilli.com/china-dictatorship/water-margin.Lenovo ThinkPad T430 running a BIOS hello world
. This uses Ciro Santilli's project x86 bare metal examples with source code at: github.com/cirosantilli/x86-bare-metal-examplesLinux Kernel Module Cheat presentation
. Source. This project, with source code at: github.com/cirosantilli/linux-kernel-module-cheat, aims to be the perfect emulation setup to study and develop the Linux kernel, kernel modules, QEMU, gem5 as well as x86_64, ARM userland and baremetal assembly and more.My Bitcoin inscription museum by Ciro Santilli
. Source. Introductory video to Section "Cool data embedded in the Bitcoin blockchain". -------------------------------------
| Force of Will 3 U U |
| --------------------------------- |
| | //////////// | |
| | ////() ()\////\ | |
| | ///_\ (--) \///\ | |
| | ) //// \_____///\\ | |
| | ) \ / / / / | |
| | ) / \ | | / _/ | |
| | ) \ ( ( / / / / \ | |
| | / ) ( ) / ( )/( ) \ | |
| | \(_)/(_)/ /UUUU \ \\\/ | | |
| .---------------------------------. |
| Interrupt |
| ,---------------------------------, |
| | You may pay 1 life and remove a | |
| | blue card in your hand from the | |
| | game instead of paying Force of | |
| | Will's casting cost. Effects | |
| | that prevent or redirect damage | |
| | cannot be used to counter this | |
| | loss of life. | |
| | Counter target spell. | |
| `---------------------------------` |
| l
| Illus. Terese Nelsen |
-------------------------------------Code 1.
ASCII art of a Force of Will Magic: The Gathering card inscribed in the Bitcoin blockchain
. Artist unknown, uploaded December 2014. Part of Section "Cool data embedded in the Bitcoin blockchain" where Ciro Santilli maintains a curated list of such interesting inscriptions.
This was a small project done by Ciro for artistic purposes that received some attention due to the incredible hype surrounding cryptocurrencies at the time. Ciro Santilli's views on cryptocurrencies are summarized at: Section "Are cryptocurrencies useful?".
YellowRobot.jpgJPG image fully embedded in the Bitcoin blockchain depicting some kind of cut material art depicting a yellow robot, inscribed on January 29, 2017.
Ciro Santilli found this image and others during his research for Section "Cool data embedded in the Bitcoin blockchain" by searching for image fingerprints on every transaction payload of the blockchain with a script.
The image was uploaded by EMBII, co-creator of the AtomSea & EMBII upload mechanism, which was responsible for a large part of the image inscriptions in the Bitcoin blockchain.
The associated message reads:This is one of Ciro Santilli's favorite AtomSea & EMBII uploads, as it perfectly encapsules the "medium as an art form" approach to blockchain art, where even non-novel works can be recontextualized into something interesting, here depicting an opposition between the ephemeral and the immutable.
Chiharu [EMBII's Japanese wife] and I found this little yellow robot while exploring Chicago. It will be covered by tar or eventually removed but this tribute will remain. N 41.880778 E -87.629210
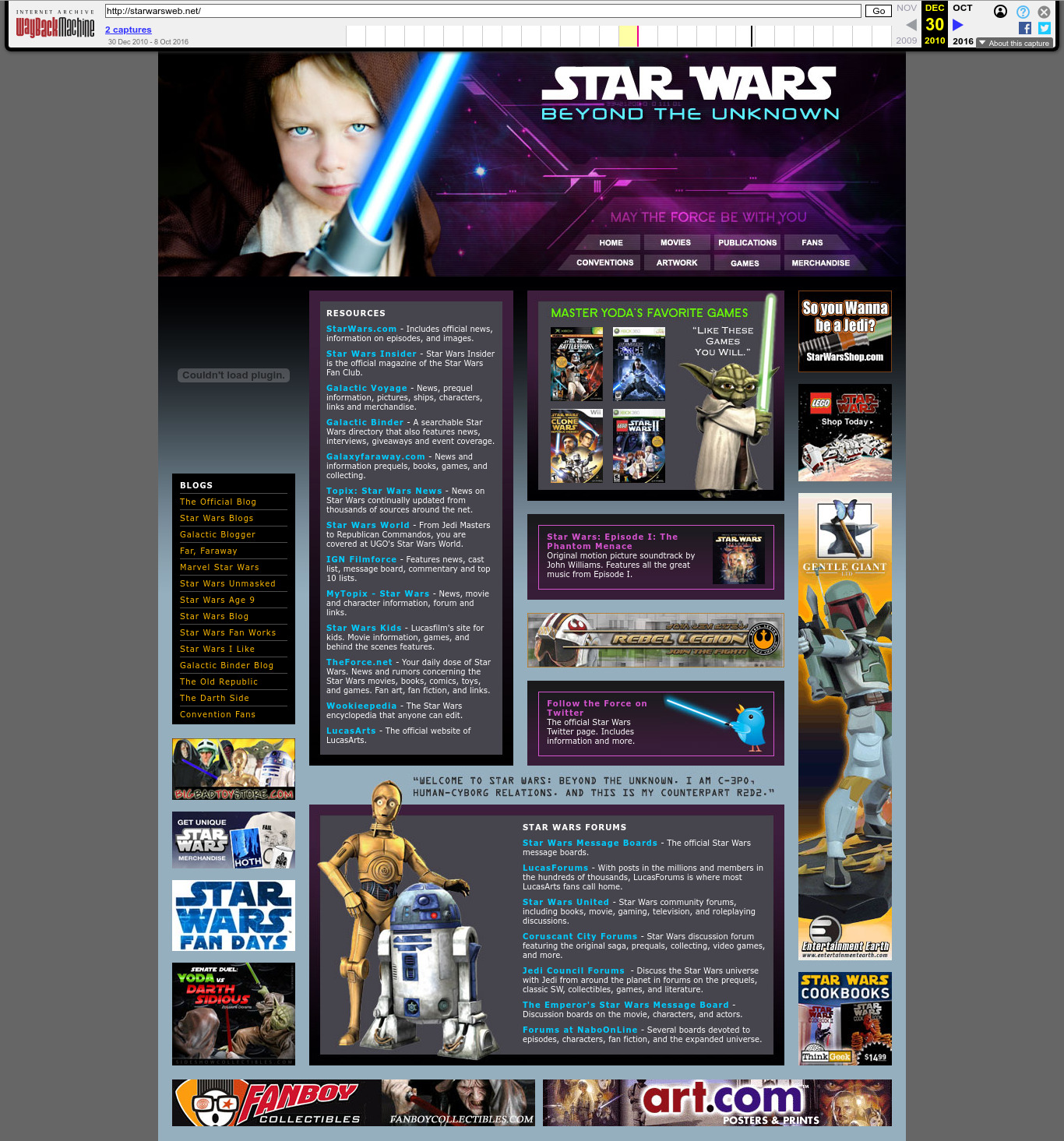
2010 Wayback Machine archive of starwarsweb.net
. This website was used as one of the CIA 2010 covert communication websites, a covert system the CIA used to communicate with its assets. More details at: Section "CIA 2010 covert communication websites".
Ciro Santilli had some naughty OSINT fun finding some of the websites of this defunct network in 2023 after he heard about the 2022 Reuters report on the matter, which for the first time gave away 7 concrete websites out of a claimed 885 total found. As of November 2023, Ciro had found about 350 of them.
2010 Wayback Machine archive of noticiasmusica.net
. This is another website that was used as one of the CIA 2010 covert communication websites. This website is written in Brazilian Portuguese, and therefore suggests that the CIA had assets in Brazil at the time, and thus was spying on a "fellow democracy".
Although Snowden's revelations made it extremely obvious to the world that the USA spies upon everyone outside of the Five Eyes, including fellow democracies, it is rare to have such a direct a concrete proof of it visible live right on the Wayback Machine. Other targeted democracies include France, Germany, Italy and Spain. More details at: USA spying on its own allies.
This investigative report by Ciro Santilli was featured on the Daily Mail after 404 Media reported on it in 2025.
Diagram of the fundamental theorem on homomorphisms by Ciro Santilli (2020)
Shows the relationship between group homomorphisms and normal subgroups.
Used in the Stack Exchange answer to What is the intuition behind normal subgroups? One of Section "The best articles by Ciro Santilli".
Spacetime diagram illustrating how faster-than-light travel implies time travel by Ciro Santilli (2021)
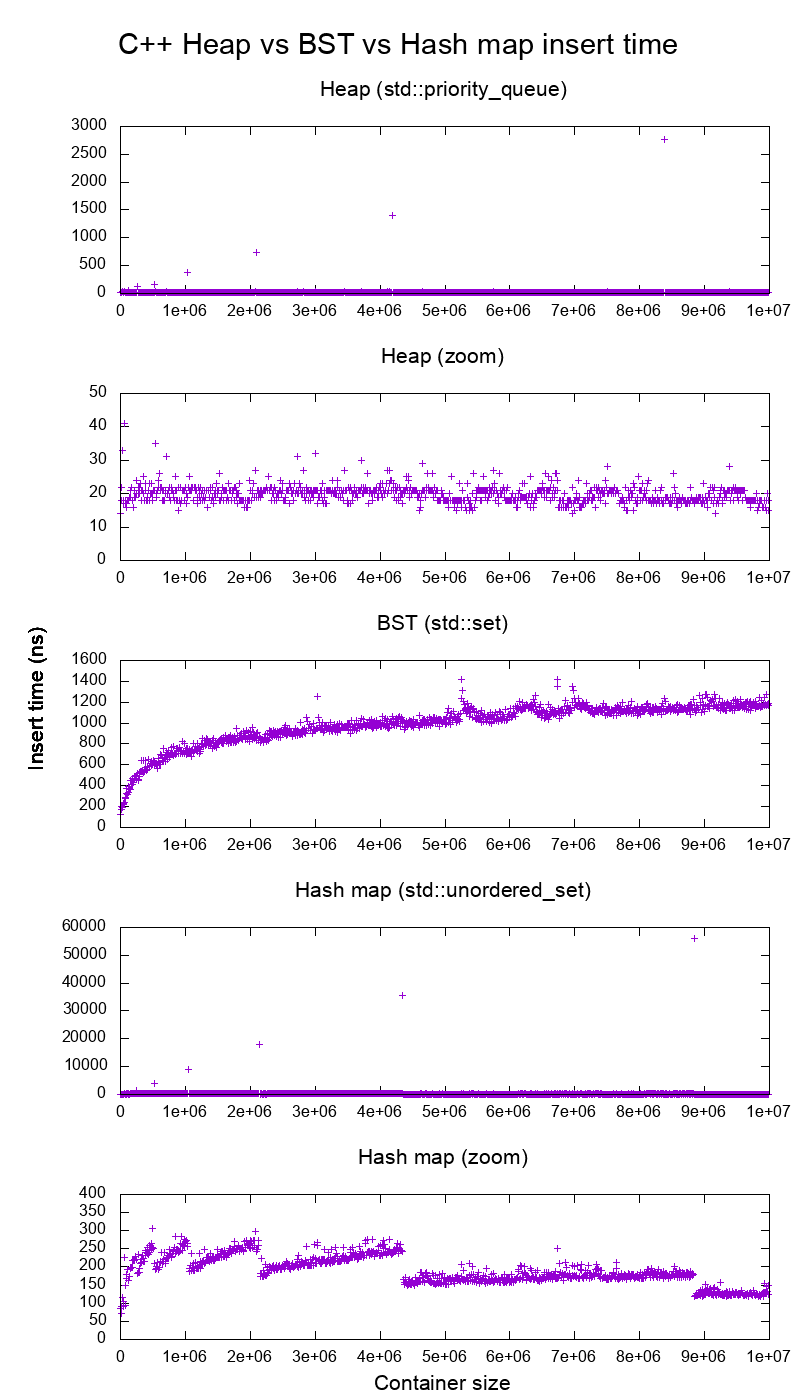
Used in the Stack Exchange answer to Does faster than light travel imply travelling back in time?. One of Section "The best articles by Ciro Santilli".Average insertion time into heaps, binary search tree and hash maps of the C++ standard library by Ciro Santilli (2015)
Source. Used in the Stack Overflow answer to Heap vs Binary Search Tree (BST). One of Section "The best articles by Ciro Santilli".Birch and Swinnerton-Dyer conjecture in two minutes by Ciro Santilli
. Source. Quick and direct explanation of the statement of the BSD conjecture for people who know basic university mathematics. This is one of the Millennium Prize Problems, and you will get a million dollars if you can solve it! This therefore falls in the Simple to state but hard to prove of Ciro Santilli's the beauty of mathematics aesthetics.Top view of an open Oxford Nanopore MinION
. Source. This is Ciro Santilli's hand on the Wikipedia article: en.wikipedia.org/wiki/Oxford_Nanopore_Technologies. He put it there after working a bit on Section "How to use an Oxford Nanopore MinION to extract DNA from river water and determine which bacteria live in it" :-) And he would love to document more experiments like that one Section "Videos of all key physics experiments", but opportunities are extremely rare.A quick 2D continuous AI game prototype for reinforcement learning written in Matter.js, you can view it on a separate page at cirosantilli.com/_raw/js/matterjs/examples.html#top-down-asdw-fixed-viewport. This is a for-fun-only prototype for Ciro's 2D reinforcement learning games, C++ or maybe Python (for the deep learning ecosystem) seems inevitable for a serious version of such a project. But it is cute how much you can do with a few lines of Matter.js!
HTML snippet:
<iframe src="_raw/js/matterjs/examples.html#top-down-asdw-fixed-viewport" width="1000" height="850"></iframe> Cool data embedded in the Bitcoin blockchain Porn Updated 2025-12-01
For now we are going to keep this site porn-free and only link to prevent bad things from happening, as it might violate GitHub porn policy depending on how it is hosted, and Google may dislike it. Video "What is more obscene: sex or war? scene from The People vs. Larry Flynt".
If illegal porn were to ever be found, we would be unable to acknowledge that, and would just have to silently remove it. Of course, the reproducible nature of Bitcoin Inscription Indexer means that anyone who regenerates the data would immediately see such entries in the diff.
Another issue is that it can be quite hard to determine if porn is legal or illegal, e.g. it can be hard to distinguish legal an illegal ages or revenge vs consensual porn, especially at the low resolutions that you may expect to find embedded in the blockchain. We are generally going to be quite strict about this, and in case of uncertainty on porn legality we will censor first.
OK the list:
- tx 4c903a377addab7c1e35a685d3dabc664199e406374b1e5ce2fc59e78fb5b754 (2016-07-09) contains an animated GIF of a woman pole dancing. She is seen from behind, in revealing blue clothes that show her buttocks. Reproduced at: twitter.com/cirosantilli/status/1755378949117370668. The file contains the following strings embedded into it:and:
This GIF file was assembled with GIF Construction Set from:
Alchemy Mindworks Inc.
This comment block will not appear in files created with a registered version of GIF Construction SetCryptograffiti.info messages now cheaper.
AI generated porn Updated 2025-12-13
This is going to be the most important application of generative AI. Especially if we ever achieve good text-to-video.
Image generators plus human ranking:
- pornpen.ai/ a bit too restrictive. Girl laying down. Girl sitting. Penis or no penis. But relatively good at it
- civitai.tv/. How to reach it: civitai.tv/tag/nun/2/
www.pornhub.com/view_video.php?viewkey=ph63c71351edece: Heavenly Bodies Part 1: Sister's Mary First Act. Pornhub title: "AI generated Hentai Story: Sexy Nun alternative World(Isekai) Stable Diffusion" Interesting concept, slide-narrated over visual novel. The question is how they managed to keep face consistency across images.
Discrete logarithm Updated 2025-10-27
An important case is the discrete logarithm of the cyclic group in which the group is a cyclic group.
Municipal Market of São Paulo Updated 2025-07-16
But as of 2020, it is completely surrounded by extremely poor people, to the point that it makes you scared if you stand out in any way by showing any kind of middle/upper class wealth, or being a foreigner.
The market is basically a touristic spot that no person in Sao Paulo will ever go to (unless they are young, single, and can just walk in there by themselves) in the middle of this surreal environment.
In 2020 Ciro was there with his wife on a touristic visit. Living in Europe at the time, he felt even more privileged. So they went to a fruit stand, and the man started giving his wife amazing free samples of very exotic fruit, some of which Ciro had never tasted himself, without saying the price. It did feel like he was giving out too much for free. Then Ciro decided of course to buy some more fruits to pay for the show, which was a nice show. Then while buying, it came out a bit more expensive than would have been reasonable, but Ciro was too dazzled by the speed and noises, and he paid for it. Later on, he told his wife about it, and how he felt that they had added some ultra-expensive bulk fruits that were of a clearly lower level than the gold nuggets of the free samples (especially for Brazil's cost standards). The presenter was an extremely crafty con artist, and Ciro felt like they had specifically preyed on Ciro Santilli's self perceived compassionate personality, because it was apparent that those men were underprivileged and fighting for their living day by day with those over-expensive fruits. This was an extremely valuable lesson, Ciro was glad that it was learnt at a relatively low cost on that occasion.
Murray Gell-Mann Updated 2025-07-16
Web of Stories 1997 interview playlist: www.youtube.com/playlist?list=PLVV0r6CmEsFxKFx-0lsQDs6oLP3SZ9BlA
The way this dude speaks. He exhales incredible intelligence!!!
In the interviews you can see that he pronounces names in all languages amazingly, making acute effort to do so, to the point of being notable. His passion for linguistics is actually mentioned on Genius: Richard Feynman and Modern Physics by James Gleick (1994).
Maybe this obsession is partly due to his name which no English speaking person knows how to pronounce from the writing.
This passion also led in part for his names to some physics terminology he worked on winning out over alternatives by his collaborators, most notably in the case of the naming of the quark.
Defining properties of elementary particles Updated 2025-07-16
A suggested at Physics from Symmetry by Jakob Schwichtenberg (2015) chapter 3.9 "Elementary particles", it appears that in the Standard Model, the behaviour of each particle can be uniquely defined by the following five numbers:
Once you specify these properties, you could in theory just pluck them into the Standard Model Lagrangian and you could simulate what happens.
Setting new random values for those properties would also allow us to create new particles. It appears unknown why we only see the particles that we do, and why they have the values of properties they have.
Definition of the exponential function Updated 2025-07-16
Definition of the indefinite orthogonal group Updated 2025-07-16
Given a matrix with metric signature containing positive and negative entries, the indefinite orthogonal group is the set of all matrices that preserve the associated bilinear form, i.e.:Note that if , we just have the standard dot product, and that subcase corresponds to the following definition of the orthogonal group: Section "The orthogonal group is the group of all matrices that preserve the dot product".
As shown at all indefinite orthogonal groups of matrices of equal metric signature are isomorphic, due to the Sylvester's law of inertia, only the metric signature of matters. E.g., if we take two different matrices with the same metric signature such as:and:both produce isomorphic spaces. So it is customary to just always pick the matrix with only +1 and -1 as entries.
Definition of the orthogonal group Updated 2025-07-16
Mathematical definition that most directly represents this: the orthogonal group is the group of all matrices that preserve the dot product.
Degree (algebra) Updated 2025-07-16
The degree of some algebraic structure is some parameter that describes the structure. There is no universal definition valid for all structures, it is a per structure type thing.
This is particularly useful when talking about structures with an infinite number of elements, but it is sometimes also used for finite structures.
Examples:
- the dihedral group of degree n acts on n elements, and has order 2n
- the parameter that characterizes the size of the general linear group is called the degree of that group, i.e. the dimension of the underlying matrices
DELETE with JOIN (SQL) Updated 2025-07-16
Demo under: nodejs/sequelize/raw/many_to_many.js.
NO way in the SQL standard apparently, but you'd hope that implementation status would be similar to UPDATE with JOIN, but not even!
- PostgreSQL: possible with
DELETE FROM USING: stackoverflow.com/questions/11753904/postgresql-delete-with-inner-join - SQLite: not possible without subqueries as of 3.35 far: stackoverflow.com/questions/24511153/how-delete-table-inner-join-with-other-table-in-sqlite, Does not appear to have any relevant features at: www.sqlite.org/lang_delete.html
ORM
- Sequelize: no support of course: stackoverflow.com/questions/40890131/sequelize-destroy-record-with-join
Deletionism Updated 2025-07-16
The problem of deletionism is that it removes users' confidence that their precious data will be safe. It's almost like having a database that constantly resets itself. Who will be willing to post on a website that deletes the content they created for free half of the time thus wasting people's precious time?
Democracy Updated 2025-07-16
Nash equilibrium Updated 2025-07-16
The best example to look at first is the penalty kick left right Nash equilibrium.
Then, a much more interesting example is choosing a deck of a TCG competition: Magic: The Gathering meta-based deck choice is a bimatrix game, which is the exact same, but each player has N choices rather than 2.
The next case that should be analyzed is the prisoner's dilemma.
The key idea is that:
- imagine that the game will be played many times between two players
- if one player always chooses one deck, the other player will adapt by choosing the anti-deck
- therefore, the best strategy for both players, is to pick decks randomly, each with a certain probability. This type of probabilistic approach is called a mixed strategy
- if any player deviates from the equilibrium probability, then the other player can add more of the anti-deck to the deck that the other player deviated, and gain an edgeTherefore, using equilibrium probabilities is the optimal way to play
Natural language processing Updated 2025-07-16
An impossible AI-complete dream!
It is impossible to understand speech, and take meaningful actions from it, if you don't understand what is being talked about.
Derivation of the Klein-Gordon equation Updated 2025-07-16
But since this is quantum mechanics, we feel like making into the "momentum operator", just like in the Schrödinger equation.
But we don't really know how to apply the momentum operator twice, because it is a gradient, so the first application goes from a scalar field to the vector field, and the second one...
But then, we have to avoid taking the square root to reach a first derivative in time, because we don't know how to take the square root of that operator expression.
So the Klein-Gordon equation just takes the approach of using this squared Hamiltonian instead.
Since it is a Hamiltonian, and comparing it to the Schrödinger equation which looks like:taking the Hamiltonian twice leads to:
We can contrast this with the Dirac equation, which instead attempts to explicitly construct an operator which squared coincides with the relativistic formula: derivation of the Dirac equation.
Derivation of the Schrodinger equation Updated 2025-07-16
Where derivation == "intuitive routes", since a "law of physics" cannot be derived, only observed right or wrong.
TODO also comment on why are complex numbers used in the Schrodinger equation?.
Some approaches:
- en.wikipedia.org/w/index.php?title=Schr%C3%B6dinger_equation&oldid=964460597#Derivation: holy crap, this just goes all in into a Lie group approach, nice
- Richard Feynman's derivation of the Schrodinger equation:
- physics.stackexchange.com/questions/263990/feynmans-derivation-of-the-schrödinger-equation
- www.youtube.com/watch?v=xQ1d0M19LsM "Class Y. Feynman's Derivation of the Schrödinger Equation" by doctorphys (2020)
- www.youtube.com/watch?v=zC_gYfAqjZY&list=PL54DF0652B30D99A4&index=53 "I5. Derivation of the Schrödinger Equation" by doctorphys
Unlisted articles are being shown, click here to show only listed articles.