Gun-type fission weapons don't work with plutonium Created 2024-08-14 Updated 2025-07-16
Gun-type fission weapons don't work with Plutonium-239 because of the presence of Plutonium-240 as an impurity which leads to fizzle.
Good mentions at: youtu.be/dgBDvnqMkT4?t=252
Gamma spectroscopy Created 2024-08-14 Updated 2025-07-16
Gamma spectroscopy of a Uranium ore
. Source. Several points of the Uranium 238 decay chain are clearly visible. Thorium-232 decay chain Created 2024-08-14 Updated 2025-07-16
Breeder reactor Created 2024-08-14 Updated 2025-07-16
A nuclear reactor made to produce specific isotopes rather than just consume fissile material to produce electrical power. The most notably application being to produce Plutonium-239 for nuclear weapons from Uranium-238 being irradiated from Uranium-235-created fission.
Tome of the Comptes rendus de l'Académie des Sciences Created 2024-08-14 Updated 2025-07-16
Weapon grade Plutonium is cheaper than weapon grade Uranium Created 2024-08-14 Updated 2025-07-16
Because you can generate plutonium-239 from uranium-238 in a breeder reactor, and then separate the plutonium-239 from the Uranium simply by using chemistry methods because you've created an element with different valence electrons.
Isn't it somewhat funny that it is easier to purify a synthetic element than a naturally occurring one?
Thorium-232 Created 2024-08-14 Updated 2025-07-16
GPHS-RTG Created 2024-08-14 Updated 2025-07-16
Polonium-209 Created 2024-08-14 Updated 2025-07-16
Polonium-208 Created 2024-08-14 Updated 2025-07-16
Plutonium-240 Created 2024-08-14 Updated 2025-07-16
This isotope shows up as an inevitable contaminant in Plutonium-239 for nuclear weapons, because it emits neutrons too fast and makes it harder to assemble the critical mass without fizzle.
It is the presence of this contaminant that made implosion-type fission weapon a necessity: Section "Gun-type fission weapons don't work with plutonium".
Plutonium-239 Created 2024-08-14 Updated 2025-07-16
Plutonium-240 is a contaminant.
Plutonium-238 Created 2024-08-14 Updated 2025-07-16
S-50 liquid thermal diffusion plant Created 2024-08-14 Updated 2025-07-16
K-25 Created 2024-08-14 Updated 2025-07-16
Y-12 electromagnetic separation plant Created 2024-08-14 Updated 2025-07-16
Thermal neutron Created 2024-08-14 Updated 2025-07-16
These are neutrons that have reached the thermal equilibrium according to the Maxwell-Boltzmann distribution after having bounced around many times without undergoing neutron capture.
Good fissile material is material that is able to absorb thermal neutrons and continue the reaction, because that's the type of neutron you end up getting the most of.
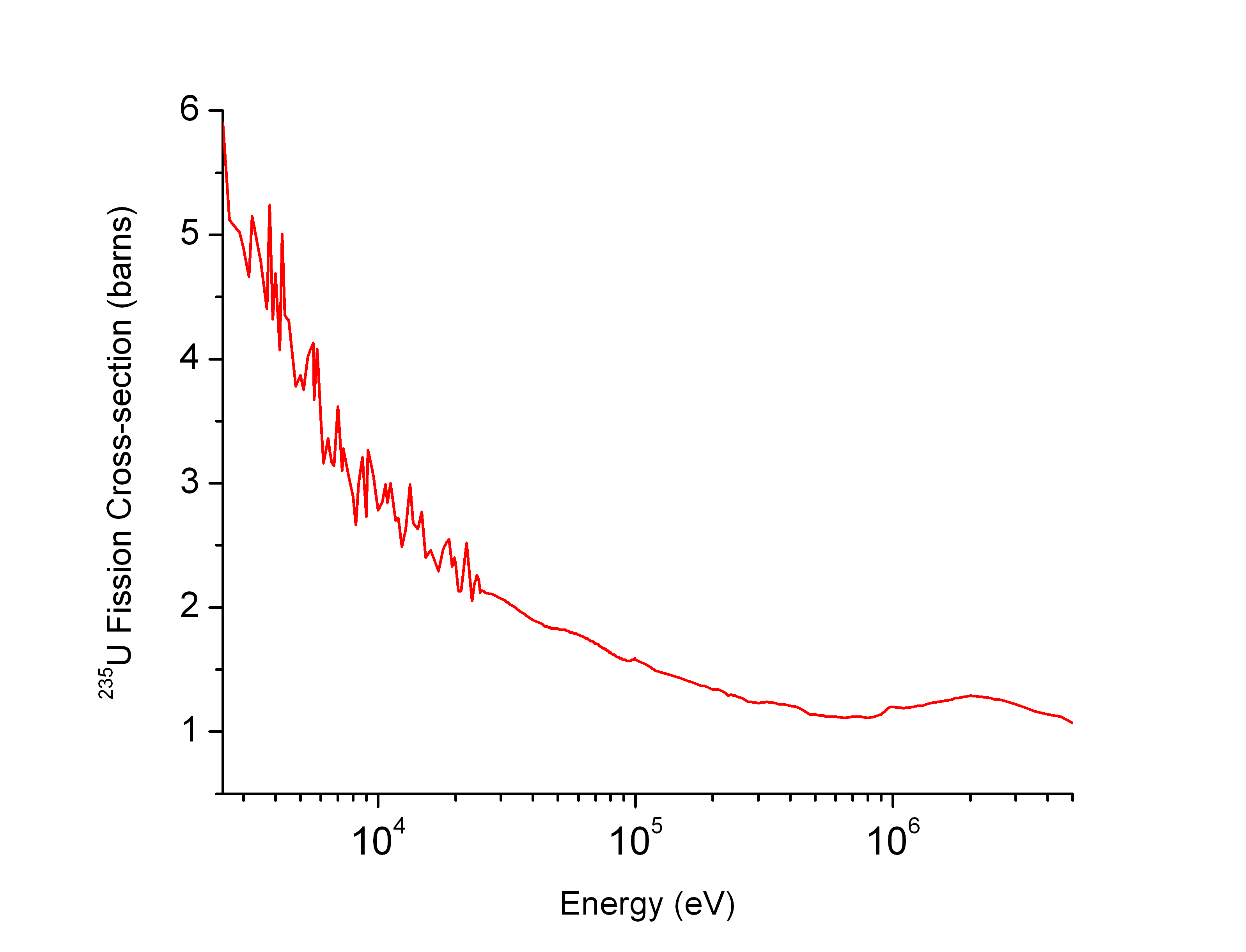
Neutron cross section Created 2024-08-14 Updated 2025-07-16
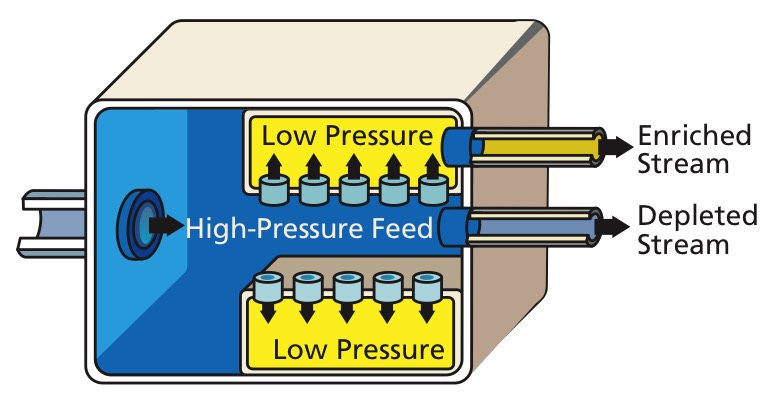
Gas centrifuge Created 2024-08-14 Updated 2025-07-16
Gaseous diffusion Created 2024-08-14 Updated 2025-07-16
This isotope separation method was the first big successful method, having been used in the Manhattan Project, notably in the K-25 reactor.
This method was superseded by the more efficient gas centrifuges.
Unlisted articles are being shown, click here to show only listed articles.