CIA 2010 covert communication websites 2013 DNS Census virtual host cleanup by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
We've noticed that often when there is a hit range:and that this does not seem to be that common. Let's see if that is a reasonable fingerprint or not.
- there is only one IP for each domain
- there is a range of about 20-30 of those
Note that although this is the most common case, we have found multiple hits that viewdns.info maps to the same IP.
First we create a table The
u (unique) that only have domains which are the only domain for an IP, let's see by how much that lowers the 191 M total unique domains:time sqlite3 u.sqlite 'create table t (d text, i text)'
time sqlite3 av.sqlite -cmd "attach 'u.sqlite' as u" "insert into u.t select min(d) as d, min(i) as i from t where d not like '%.%.%' group by i having count(distinct d) = 1"not like '%.%.%' removes subdomains from the counts so that CGI comms are still included, and distinct in count(distinct is because we have multiple entries at different timestamps for some of the hits.Let's start with the 208 subset to see how it goes:OK, after we fixed bugs with the above we are down to 4 million lines with unique domain/IP pairs and which contains all of the original hits! Almost certainly more are to be found!
time sqlite3 av.sqlite -cmd "attach 'u.sqlite' as u" "insert into u.t select min(d) as d, min(i) as i from t where i glob '208.*' and d not like '%.%.%' and (d like '%.com' or d like '%.net') group by i having count(distinct d) = 1"This data is so valuable that we've decided to upload it to: archive.org/details/2013-dns-census-a-novirt.csv Format:The numbers of the first column are the IPs as a 32-bit integer representation, which is more useful to search for ranges in.
8,chrisjmcgregor.com
11,80end.com
28,fine5.net
38,bestarabictv.com
49,xy005.com
50,cmsasoccer.com
80,museemontpellier.net
100,newtiger.com
108,lps-promptservice.com
111,bridesmaiddressesshow.comTo make a histogram with the distribution of the single hostname IPs:Which gives the following useless noise, there is basically no pattern:
#!/usr/bin/env bash
bin=$((2**24))
sqlite3 2013-dns-census-a-novirt.sqlite -cmd '.mode csv' >2013-dns-census-a-novirt-hist.csv <<EOF
select i, sum(cnt) from (
select floor(i/${bin}) as i,
count(*) as cnt
from t
group by 1
union
select *, 0 as cnt from generate_series(0, 255)
)
group by i
EOF
gnuplot \
-e 'set terminal svg size 1200, 800' \
-e 'set output "2013-dns-census-a-novirt-hist.svg"' \
-e 'set datafile separator ","' \
-e 'set tics scale 0' \
-e 'unset key' \
-e 'set xrange[0:255]' \
-e 'set title "Counts of IPs with a single hostname"' \
-e 'set xlabel "IPv4 first byte"' \
-e 'set ylabel "count"' \
-e 'plot "2013-dns-census-a-novirt-hist.csv" using 1:2:1 with labels' \
; CIA 2010 covert communication websites 2013 DNS census MX records by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
Let' see if there's anything in records/mx.xz.
mx.csv is 21GB.
They do have
" in the files to escape commas so:mx.pyWould have been better with csvkit: stackoverflow.com/questions/36287982/bash-parse-csv-with-quotes-commas-and-newlines
import csv
import sys
writer = csv.writer(sys.stdout)
with open('mx.csv', 'r') as f:
reader = csv.reader(f)
for row in reader:
writer.writerow([row[0], row[3]])then:
# uniq not amazing as there are often two or three slightly different records repeated on multiple timestamps, but down to 11 GB
python3 mx.py | uniq > mx-uniq.csv
sqlite3 mx.sqlite 'create table t(d text, m text)'
# 13 GB
time sqlite3 mx.sqlite ".import --csv --skip 1 'mx-uniq.csv' t"
# 41 GB
time sqlite3 mx.sqlite 'create index td on t(d)'
time sqlite3 mx.sqlite 'create index tm on t(m)'
time sqlite3 mx.sqlite 'create index tdm on t(d, m)'
# Remove dupes.
# Rows: 150m
time sqlite3 mx.sqlite <<EOF
delete from t
where rowid not in (
select min(rowid)
from t
group by d, m
)
EOF
# 15 GB
time sqlite3 mx.sqlite vacuumLet's see what the hits use:
awk -F, 'NR>1{ print $2 }' ../media/cia-2010-covert-communication-websites/hits.csv | xargs -I{} sqlite3 mx.sqlite "select distinct * from t where d = '{}'"At around 267 total hits, only 84 have MX records, and from those that do, almost all of them have exactly:with only three exceptions:We need to count out of the totals!which gives, ~18M, so nope, it is too much by itself...
smtp.secureserver.net
mailstore1.secureserver.netdailynewsandsports.com|dailynewsandsports.com
inews-today.com|mail.inews-today.com
just-kidding-news.com|just-kidding-news.comsqlite3 mx.sqlite "select count(*) from t where m = 'mailstore1.secureserver.net'"Let's try to use that to reduce where
av.sqlite from 2013 DNS Census virtual host cleanup a bit further:time sqlite3 mx.sqlite '.mode csv' "attach 'aiddcu.sqlite' as 'av'" '.load ./ip' "select ipi2s(av.t.i), av.t.d from av.t inner join t as mx on av.t.d = mx.d and mx.m = 'mailstore1.secureserver.net' order by av.t.i asc" > avm.csvavm stands for av with mx pruning. This leaves us with only ~500k entries left. With one more figerprint we could do a Wayback Machine CDX scanning scan.Let's check that we still have most our hits in there:At 267 hits we got 81, so all are still present.
grep -f <(awk -F, 'NR>1{print $2}' /home/ciro/bak/git/media/cia-2010-covert-communication-websites/hits.csv) avm.csvsecureserver is a hosting provider, we can see their blank page e.g. at: web.archive.org/web/20110128152204/http://emmano.com/. security.stackexchange.com/questions/12610/why-did-secureserver-net-godaddy-access-my-gmail-account/12616#12616 comments:
secureserver.net is the name GoDaddy use as the reverse DNS for IP addresses used for dedicated/virtual server hosting
CIA 2010 covert communication websites 2013 DNS census NS records by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
We can also cut down the data a lot with stackoverflow.com/questions/1915636/is-there-a-way-to-uniq-by-column/76605540#76605540 and tld filtering:This brings us down to a much more manageable 3.0 GB, 83 M rows.
awk -F, 'BEGIN{OFS=","} { if ($1 != last) { print $1, $3; last = $1; } }' ns.csv | grep -E '\.(com|net|info|org|biz),' > nsu.csvLet's just scan it once real quick to start with, since likely nothing will come of this venue:As of 267 hits we get:so yeah, most of those are likely going to be humongous just by looking at the names.
grep -f <(awk -F, 'NR>1{print $2}' ../media/cia-2010-covert-communication-websites/hits.csv) nsu.csv | tee nsu-hits.csv
cat nsu-hits.csv | csvcut -c 2 | sort | awk -F. '{OFS="."; print $(NF-1), $(NF)}' | sort | uniq -c | sort -k1 -n 1 a2hosting.com
1 amerinoc.com
1 ayns.net
1 dailyrazor.com
1 domainingdepot.com
1 easydns.com
1 frienddns.ru
1 hostgator.com
1 kolmic.com
1 name-services.com
1 namecity.com
1 netnames.net
1 tonsmovies.net
1 webmailer.de
2 cashparking.com
55 worldnic.com
86 domaincontrol.comThe smallest ones by far from the total are: frienddns.ru with only 487 hits, all others quite large or fake hits due to CSV. Did a quick Wayback Machine CDX scanning there but no luck alas.
Let's check the smaller ones:Doubt anything will come out of this.
inews-today.com,2013-08-12T03:14:01,ns1.frienddns.ru
source-commodities.net,2012-12-13T20:58:28,ns1.namecity.com -> fake hit due to grep e-commodities.net
dailynewsandsports.com,2013-08-13T08:36:28,ns3.a2hosting.com
just-kidding-news.com,2012-02-04T07:40:50,jns3.dailyrazor.com
fightwithoutrules.com,2012-11-09T01:17:40,sk.s2.ns1.ns92.kolmic.com
fightwithoutrules.com,2013-07-01T22:46:23,ns1625.ztomy.com
half-court.net,2012-09-10T09:49:15,sk.s2.ns1.ns92.kolmic.com
half-court.net,2013-07-07T00:31:12,ns1621.ztomy.com CIA 2010 covert communication websites 2013 DNS census SOA records by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
Same as 2013 DNS census NS records basically, nothing came out.
CIA 2010 covert communication websites 2012 Internet Census hostprobes by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
Hostprobes quick look on two ranges:
208.254.40:
... similar down
208.254.40.95 1334668500 down no-response
208.254.40.95 1338270300 down no-response
208.254.40.95 1338839100 down no-response
208.254.40.95 1339361100 down no-response
208.254.40.95 1346391900 down no-response
208.254.40.96 1335806100 up unknown
208.254.40.96 1336979700 up unknown
208.254.40.96 1338840900 up unknown
208.254.40.96 1339454700 up unknown
208.254.40.96 1346778900 up echo-reply (0.34s latency).
208.254.40.96 1346838300 up echo-reply (0.30s latency).
208.254.40.97 1335840300 up unknown
208.254.40.97 1338446700 up unknown
208.254.40.97 1339334100 up unknown
208.254.40.97 1346658300 up echo-reply (0.26s latency).
... similar up
208.254.40.126 1335708900 up unknown
208.254.40.126 1338446700 up unknown
208.254.40.126 1339330500 up unknown
208.254.40.126 1346494500 up echo-reply (0.24s latency).
208.254.40.127 1335840300 up unknown
208.254.40.127 1337793300 up unknown
208.254.40.127 1338853500 up unknown
208.254.40.127 1346454900 up echo-reply (0.23s latency).
208.254.40.128 1335856500 up unknown
208.254.40.128 1338200100 down no-response
208.254.40.128 1338749100 down no-response
208.254.40.128 1339334100 down no-response
208.254.40.128 1346607900 down net-unreach
208.254.40.129 1335699900 up unknown
... similar downSuggests exactly 127 - 96 + 1 = 31 IPs.
208.254.42:
... similar down
208.254.42.191 1334522700 down no-response
208.254.42.191 1335276900 down no-response
208.254.42.191 1335784500 down no-response
208.254.42.191 1337845500 down no-response
208.254.42.191 1338752700 down no-response
208.254.42.191 1339332300 down no-response
208.254.42.191 1346499900 down net-unreach
208.254.42.192 1334668500 up unknown
208.254.42.192 1336808700 up unknown
208.254.42.192 1339334100 up unknown
208.254.42.192 1346766300 up echo-reply (0.40s latency).
208.254.42.193 1335770100 up unknown
208.254.42.193 1338444900 up unknown
208.254.42.193 1339334100 up unknown
... similar up
208.254.42.221 1346517900 up echo-reply (0.19s latency).
208.254.42.222 1335708900 up unknown
208.254.42.222 1335708900 up unknown
208.254.42.222 1338066900 up unknown
208.254.42.222 1338747300 up unknown
208.254.42.222 1346872500 up echo-reply (0.27s latency).
208.254.42.223 1335773700 up unknown
208.254.42.223 1336949100 up unknown
208.254.42.223 1338750900 up unknown
208.254.42.223 1339334100 up unknown
208.254.42.223 1346854500 up echo-reply (0.13s latency).
208.254.42.224 1335665700 down no-response
208.254.42.224 1336567500 down no-response
208.254.42.224 1338840900 down no-response
208.254.42.224 1339425900 down no-response
208.254.42.224 1346494500 down time-exceeded
... similar downSuggests exactly 223 - 192 + 1 = 31 IPs.
It does appears that long sequences of ranges are a sort of fingerprint. The question is how unique it would be.
First:This reduces us to 2 million IP rows from the total possible 16 million IPs.
n=208
time awk '$3=="up"{ print $1 }' $n | uniq -c | sed -r 's/^ +//;s/ /,/' | tee $n-up-uniq
t=$n-up-uniq.sqlite
rm -f $t
time sqlite3 $t 'create table tmp(cnt text, i text)'
time sqlite3 $t ".import --csv $n-up-uniq tmp"
time sqlite3 $t 'create table t (i integer)'
time sqlite3 $t '.load ./ip' 'insert into t select str2ipv4(i) from tmp'
time sqlite3 $t 'drop table tmp'
time sqlite3 $t 'create index ti on t(i)'OK now just counting hits on fixed windows has way too many results:
sqlite3 208-up-uniq.sqlite "\
SELECT * FROM (
SELECT min(i), COUNT(*) OVER (
ORDER BY i RANGE BETWEEN 15 PRECEDING AND 15 FOLLOWING
) as c FROM t
) WHERE c > 20 and c < 30
"Let's try instead consecutive ranges of length exactly 31 instead then:271. Hmm. A bit more than we'd like...
sqlite3 208-up-uniq.sqlite <<EOF
SELECT f, t - f as c FROM (
SELECT min(i) as f, max(i) as t
FROM (SELECT i, ROW_NUMBER() OVER (ORDER BY i) - i as grp FROM t)
GROUP BY grp
ORDER BY i
) where c = 31
EOFAnother route is to also count the ups:
n=208
time awk '$3=="up"{ print $1 }' $n | uniq -c | sed -r 's/^ +//;s/ /,/' | tee $n-up-uniq-cnt
t=$n-up-uniq-cnt.sqlite
rm -f $t
time sqlite3 $t 'create table tmp(cnt text, i text)'
time sqlite3 $t ".import --csv $n-up-uniq-cnt tmp"
time sqlite3 $t 'create table t (cnt integer, i integer)'
time sqlite3 $t '.load ./ip' 'insert into t select cnt as integer, str2ipv4(i) from tmp'
time sqlite3 $t 'drop table tmp'
time sqlite3 $t 'create index ti on t(i)'Let's see how many consecutives with counts:
sqlite3 208-up-uniq-cnt.sqlite <<EOF
SELECT f, t - f as c FROM (
SELECT min(i) as f, max(i) as t
FROM (SELECT i, ROW_NUMBER() OVER (ORDER BY i) - i as grp FROM t WHERE cnt >= 3)
GROUP BY grp
ORDER BY i
) where c > 28 and c < 32
EOFLet's check on 66:not representative at all... e.g. several convfirmed hits are down:
grep -e '66.45.179' -e '66.45.179' 6666.45.179.215 1335305700 down no-response
66.45.179.215 1337579100 down no-response
66.45.179.215 1338765300 down no-response
66.45.179.215 1340271900 down no-response
66.45.179.215 1346813100 down no-response CIA 2010 covert communication websites 2012 Internet Census icmp_ping by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
Let's check relevancy of known hits:Output:
grep -e '208.254.40' -e '208.254.42' 208 | tee 208hits208.254.40.95 1355564700 unreachable
208.254.40.95 1355622300 unreachable
208.254.40.96 1334537100 alive, 36342
208.254.40.96 1335269700 alive, 17586
..
208.254.40.127 1355562900 alive, 35023
208.254.40.127 1355593500 alive, 59866
208.254.40.128 1334609100 unreachable
208.254.40.128 1334708100 alive from 208.254.32.214, 43358
208.254.40.128 1336596300 unreachableThe rest of 208 is mostly unreachable.
208.254.42.191 1335294900 unreachable
...
208.254.42.191 1344737700 unreachable
208.254.42.191 1345574700 Icmp Error: 0,ICMP Network Unreachable, from 63.111.123.26
208.254.42.191 1346166900 unreachable
...
208.254.42.191 1355665500 unreachable
208.254.42.192 1334625300 alive, 6672
...
208.254.42.192 1355658300 alive, 57412
208.254.42.193 1334677500 alive, 28985
208.254.42.193 1336524300 unreachable
208.254.42.193 1344447900 alive, 8934
208.254.42.193 1344613500 alive, 24037
208.254.42.193 1344806100 alive, 20410
208.254.42.193 1345162500 alive, 10177
...
208.254.42.223 1336590900 alive, 23284
...
208.254.42.223 1355555700 alive, 58841
208.254.42.224 1334607300 Icmp Type: 11,ICMP Time Exceeded, from 65.214.56.142
208.254.42.224 1334681100 Icmp Type: 11,ICMP Time Exceeded, from 65.214.56.142
208.254.42.224 1336563900 Icmp Type: 11,ICMP Time Exceeded, from 65.214.56.142
208.254.42.224 1344451500 Icmp Type: 11,ICMP Time Exceeded, from 65.214.56.138
208.254.42.224 1344566700 unreachable
208.254.42.224 1344762900 unreachablen=66
time awk '$3~/^alive,/ { print $1 }' $n | uniq -c | sed -r 's/^ +//;s/ /,/' | tee $n-up-uniq-cOK down to 45 MB, now we can work.
grep -e '66.45.179' -e '66.104.169' -e '66.104.173' -e '66.104.175' -e '66.175.106' '66-alive-uniq-c' | tee 66hitsThere are two types of JavaScript found so far. The ones with SHA and the ones without. There are only 2 examples of JS with SHA:Both files start with precisely the same string:
- iraniangoals.com: web.archive.org/web/20110202091909/http://iraniangoals.com/journal.js Commented at: iraniangoals.com JavaScript reverse engineering
- iranfootballsource.com: web.archive.org/web/20110202091901/http://iranfootballsource.com/futbol.js
- kukrinews.com: web.archive.org/web/20100513094909/http://kukrinews.com/news.js
- todaysnewsandweather-ru.com: web.archive.org/web/20110207094735/http://todaysnewsandweather-ru.com/blacksea.js
var ms="\u062F\u0631\u064A\u0627\u0641\u062A\u06CC",lc="\u062A\u0647\u064A\u0647 \u0645\u062A\u0646",mn="\u0628\u0631\u062F\u0627\u0632\u0634 \u062F\u0631 \u062C\u0631\u064A\u0627\u0646 \u0627\u0633\u062A...\u0644\u0637\u0641\u0627 \u0635\u0628\u0631 \u0643\u0646\u064A\u062F",lt="\u062A\u0647\u064A\u0647 \u0645\u062A\u0646",ne="\u067E\u0627\u0633\u062E",kf="\u062E\u0631\u0648\u062C",mb="\u062D\u0630\u0641",mv="\u062F\u0631\u064A\u0627\u0641\u062A\u06CC",nt="\u0627\u0631\u0633\u0627\u0644",ig="\u062B\u0628\u062A \u063A\u0644\u0637. \u062C\u0647\u062A \u062A\u062C\u062F\u064A\u062F \u062B\u0628\u062A \u0635\u0641\u062D\u0647 \u0631\u0627 \u0628\u0627\u0632\u0622\u0648\u0631\u06CC \u06A9\u0646\u064A\u062F",hs="\u063A\u064A\u0631 \u0642\u0627\u0628\u0644 \u0627\u062C\u0631\u0627. \u062E\u0637\u0627 \u062F\u0631 \u0627\u062A\u0651\u0635\u0627\u0644",ji="\u063A\u064A\u0631 \u0642\u0627\u0628\u0644 \u0627\u062C\u0631\u0627. \u062E\u0637\u0627 \u062F\u0631 \u0627\u062A\u0651\u0635\u0627\u0644",ie="\u063A\u064A\u0631 \u0642\u0627\u0628\u0644 \u0627\u062C\u0631\u0627. \u062E\u0637\u0627 \u062F\u0631 \u0627\u062A\u0651\u0635\u0627\u0644",gc="\u0633\u0648\u0627\u0631 \u06A9\u0631\u062F\u0646 \u062A\u06A9\u0645\u064A\u0644 \u0634\u062F",gz="\u0645\u0637\u0645\u0626\u0646\u064A\u062F \u06A9\u0647 \u0645\u064A\u062E\u0648\u0627\u0647\u064A\u062F \u067E\u064A\u0627\u0645 \u0631\u0627 \u062D\u0630\u0641 \u06A9\u0646\u064A\u062F\u061F"Good fingerprint present in all of them:
throw new Error("B64 D.1");};if(at[1]==-1){throw new Error("B64 D.2");};if(at[2]==-1){if(f<ay.length){throw new Error("B64 D.3");};dg=2;}else if(at[3]==-1){if(f<ay.length){throw new Error("B64 D.4") CIA 2010 covert communication websites feedsdemexicoyelmundo.com JavaScript reverse engineering by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
The JavaScript of each website appears to be quite small and similarly sized. They are all minimized, but have reordered things around a bit.
For example consider: web.archive.org/web/20110202190932/http://feedsdemexicoyelmundo.com/mundo.js
First we have to know that the Wayback Machine adds some stuff before and after the original code. The actual code there starts at:and ends in:
ap={fg:['MSXML2.XMLHTTPck++;};return fu;};Further analysis would be needed.
Previously it was unclear if there were any .org hits, until we found the first one with clear comms: web.archive.org/web/20110624203548/http://awfaoi.org/hand.jar
Later on, two more clear ones were found with expired domain trackers:further settling their existence. Later on newimages.org also came to light.
Others that had been previously found in IP ranges but without clear comms:
.org is very rare, and has been excluded from some of our search heuristics. That was a shame, but likely not much was missed.
CIA 2010 covert communication websites Wayback Machine CDX scanning by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
The Wayback Machine has an endpoint to query cralwed pages called the CDX server. It is documented at: github.com/internetarchive/wayback/blob/master/wayback-cdx-server/README.md.
This allows to filter down 10 thousands of possible domains in a few hours. But 100s of thousands would be too much. This is because you have to query exactly one URL at a time, and they possibly rate limit IPs. But no IP blacklisting so far after several hours, so it's not that bad.
Once you have a heuristic to narrow down some domains, you can use this helper: ../cia-2010-covert-communication-websites/cdx.sh to drill them down from 10s of thousands down to hundreds or thousands.
We then post process the results of cdx.sh with ../cia-2010-covert-communication-websites/cdx-post.sh to drill them down from from thousands to dozens, and manually inspect everything.
From then on, you can just manually inspect for hist on your browser.
CIA 2010 covert communication websites Wayback Machine crawl date search by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
At twitter.com/togelius/status/1328404390114435072 called out on DeepMind Lab2D for not giving them credit on prior work!As seen from web.archive.org/web/20220331022932/http://gvgai.net/ though, DeepMind sponsored them at some point.
This very much looks like like GVGAI which was first released in 2014, been used in dozens (maybe hundreds) of papers, and for which one of the original developers was Tom Schaul at DeepMind...
- SQLite with
rowid: stackoverflow.com/questions/8190541/deleting-duplicate-rows-from-sqlite-database - SQL Server has crazy "CTEs" change backing table extension: stackoverflow.com/questions/18390574/how-to-delete-duplicate-rows-in-sql-server
Principal investigator: Simon M. Lucas.
diff3 conflict is basically what you always want to see, either by setting it as the default as per stackoverflow.com/questions/27417656/should-diff3-be-default-conflictstyle-on-git:git config --global merge.conflictstyle diff3git checkout --conflict=diff3With this, conflicts now show up as:
++<<<<<<< HEAD
+5
++||||||| parent of 7b0f59d (6)
++3
++=======
+ 6
++>>>>>>> 7b0f59d (6)7b0f59d is the SHA-2 of commit 6.instead of the inferior default:
++<<<<<<< ours
+5
++=======
+ 6
++>>>>>>> theirsWe can also observe the current tree state during resolution:so we understand that we are now at 5 and that we are trying to apply our commit
* b4ec057 (HEAD, master) 5
* 0b37c1b 4
| * fbfbfe8 (my-feature) 7
| * 7b0f59d 6
|/
* 661cfab 3
* 6d748a9 2
* c5f8a2c 16So it is much clearer what is happening:and so now we have to decide what the new code is that will put both of these together.
We now reach:and the tree looks like:So we understand that:
++<<<<<<< HEAD
+11
++||||||| parent of fbfbfe8 (7)
++6
++=======
+ 7
++>>>>>>> fbfbfe8 (7)* ca7f7ff (HEAD) 6
* b4ec057 (master) 5
* 0b37c1b 4
| * fbfbfe8 (my-feature) 7
| * 7b0f59d 6
|/
* 661cfab 3
* 6d748a9 2
* c5f8a2c 1and after resolving that one we now reach:
* e1aaf20 (HEAD -> my-feature) 7
* ca7f7ff 6
* b4ec057 (master) 5
* 0b37c1b 4
* 661cfab 3
* 6d748a9 2
* c5f8a2c 1These are good free newbie GUI options:
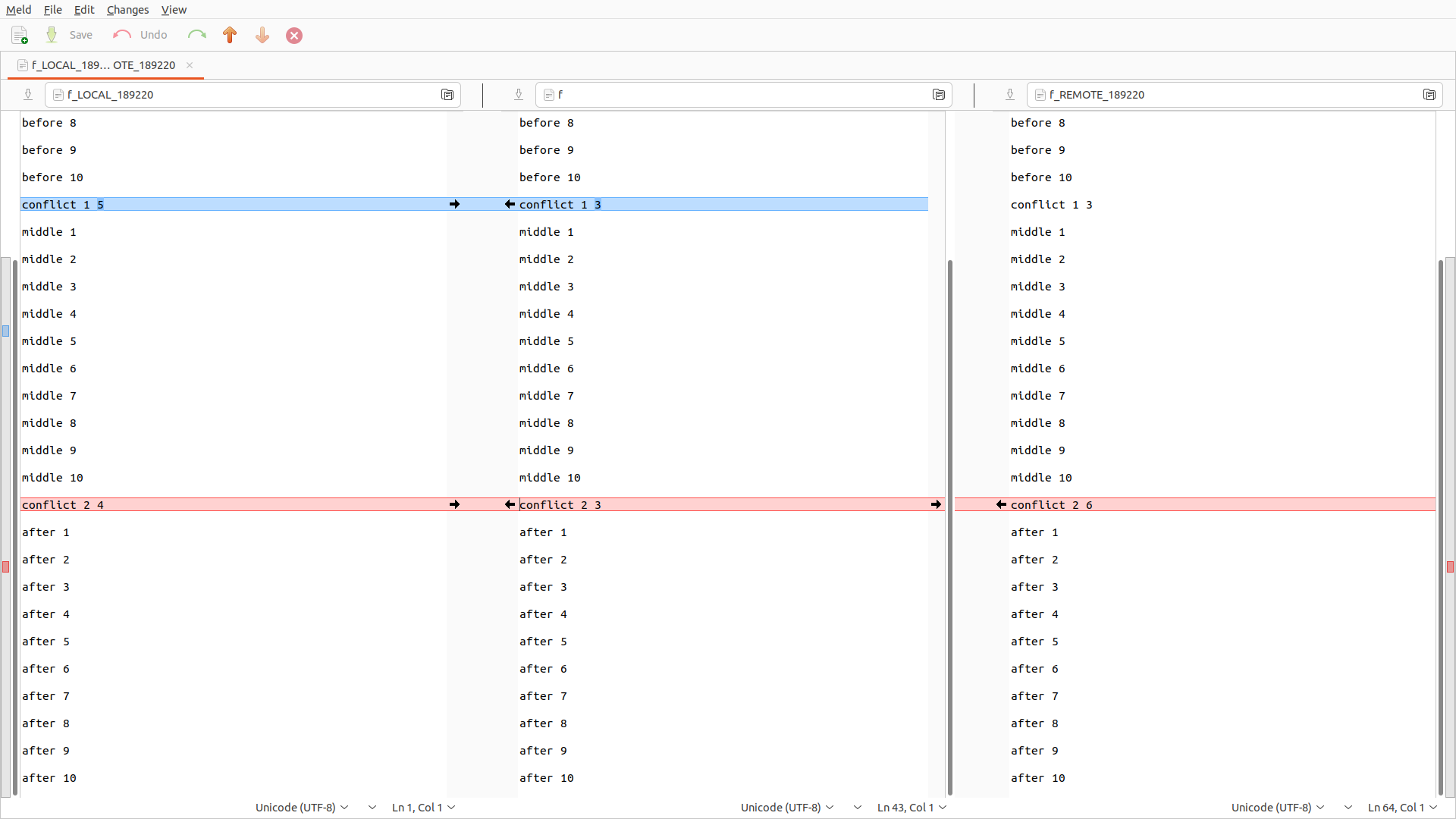
sudo apt install meld
git mergetool --tool meld
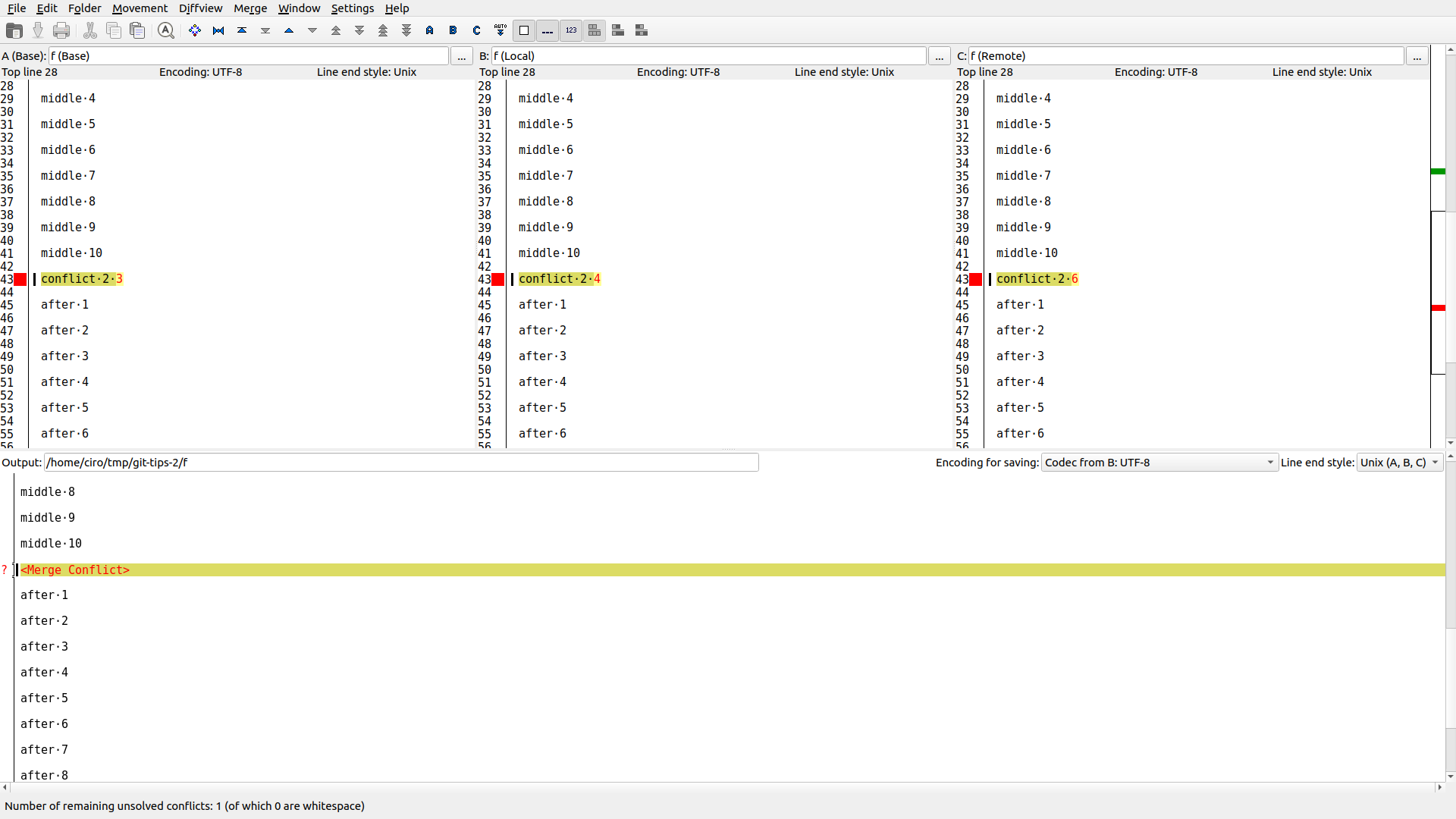
sudo apt install kdiff3
git mergetool --tool kdiff3git-tips-2.sh
#!/usr/bin/env bash
set -eux
add() (
rm -f f
for i in `seq 10`; do
printf "before $i\n\n" >> f
done
printf "conflict 1 $1\n\n" >> f
for i in `seq 10`; do
printf "middle $i\n\n" >> f
done
printf "conflict 2 $2\n\n" >> f
for i in `seq 10`; do
printf "after $i\n\n" >> f
done
git add f
)
rm -rf git-tips-2
mkdir git-tips-2
cd git-tips-2
git init
for i in 1 2 3; do
add $i $i
git commit -m $i
done
add 3 4
git commit -m 4
add 5 4
git commit -m 5
git checkout HEAD~2
git checkout -b my-feature
add 3 6
git commit -m 6
add 7 6
git commit -m 7 Git tips But which commit from master did we conflict with exactly? by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
git rebase does not tell you that, and that sucks.We only know which commit from the feature branch caused the problem.
Generally we can guess or it is not needed, but
imerge does look promising: stackoverflow.com/questions/18162930/how-can-i-find-out-which-git-commits-cause-conflicts There are unlisted articles, also show them or only show them.