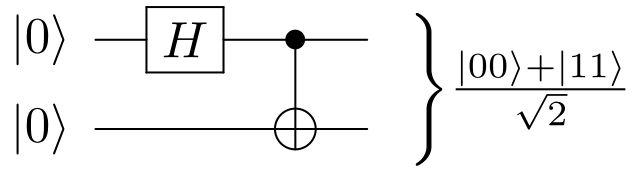
Ciro Santilli (@cirosantilli) - undefined articles

Bell circuit  Updated 2024-12-15  +Created 1970-01-01

A quantum circuit which when fed with input

∣ 00 ⟩

produces the Bell state.

In Qiskit at: qiskit/hello.py.

Figure 1.
Quantum circuit that generates the Bell state
. Source.
The fundamental intuition for this circuit is as follows.
First the Hadamard gate makes the first qubit be in a 50/50 state.
Then, the CNOT gate gets controlled by that 50/50 value, and the controlled qubit also gets 50/50 chance as a result.
However, both qubits are now entangled: the result of the second qubit depends on the result of the first one. Because:
if the first qubit is 0, cnot is not active, and so the second qubit remains 0 as its input
if the first qubit is 1, cnot is active, and so the second qubit is flipped to 1

 Read the full article

CNOT gate  Updated 2024-12-15  +Created 1970-01-01

 View more

The CNOT gate is a controlled quantum gate that operates on two qubits, flipping the second (operand) qubit if the first (control) qubit is set.

This gate is the first example of a controlled quantum gate that you should study.

⎣ ⎢ ⎢ ⎢ ⎡ 1000010000010010 ⎦ ⎥ ⎥ ⎥ ⎤

(1)

Equation 1.

CNOT gate matrix

.

Figure 1.
CNOT gate symbol
. Source. The symbol follow the generic symbol convention for controlled quantum gates shown at Figure "Generic controlled quantum gate symbol", but replacing the generic "U" with the Figure "Quantum NOT gate symbol".

To understand why the gate is called a CNOT gate, you should think as follows.

First let's produce a generic quantum state vector where the control qubit is certain to be 0.

On the standard basis:

∣ 00 ⟩ ∣ 01 ⟩ ∣ 10 ⟩ ∣ 11 ⟩

(2)

we see that this means that only

∣ 00 ⟩

and

∣ 01 ⟩

should be possible. Therefore, the state must be of the form:

⎣ ⎢ ⎢ ⎢ ⎡ x y 00 ⎦ ⎥ ⎥ ⎥ ⎤

(3)

where

x

and

y

are two complex numbers such that

∣ x ∣ + ∣ y ∣ = 1.0

If we operate the CNOT gate on that state, we obtain:

⎣ ⎢ ⎢ ⎢ ⎡ 1000010000010010 ⎦ ⎥ ⎥ ⎥ ⎤ \times ⎣ ⎢ ⎢ ⎢ ⎡ x y 00 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ x y 00 ⎦ ⎥ ⎥ ⎥ ⎤

(4)

and so the input is unchanged as desired, because the control qubit is 0.

If however we take only states where the control qubit is for sure 1:

⎣ ⎢ ⎢ ⎢ ⎡ 1000010000010010 ⎦ ⎥ ⎥ ⎥ ⎤ \times ⎣ ⎢ ⎢ ⎢ ⎡ 00 x y ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ 00 y x ⎦ ⎥ ⎥ ⎥ ⎤

(5)

Therefore, in that case, what happened is that the probabilities of

∣ 10 ⟩

and

∣ 11 ⟩

were swapped from

x

and

y

to

y

and

x

respectively, which is exactly what the quantum NOT gate does.

So from this we understand more concretely what "the gate only operates if the first qubit is set to one" means.

Now go and study the Bell state and understand intuitively how this gate is used to produce it.

 Read the full article

Controlled quantum gate  Updated 2024-12-15  +Created 1970-01-01

 View more

Controlled quantum gates are gates that have two types of input qubits:

control qubits
operand qubits (terminology made up by Ciro Santilli just now)

These gates can be understood as doing a certain unitary operation only if the control qubits are enabled or disabled.

The first example to look at is the CNOT gate.

Figure 1.
Generic controlled quantum gate symbol
. Source.
The black dot means "control qubit", and "U" means an arbitrary Unitary operation.
When the operand has a conventional symbol, e.g. the Figure "Quantum NOT gate symbol" for the quantum NOT gate to form the CNOT gate, that symbol is used in the operand instead.

 Read the full article

@cirosantilli/_file/qiskit/qiskit/hello.py  Updated 2024-12-15  +Created 1970-01-01

 View more

Our example uses a Bell state circuit to illustrate all the fundamental Qiskit basics.

Sample program output, counts are randomized each time.

First we take the quantum state vector immediately after the

∣ 00 ⟩

input.

input:
state:
Statevector([1.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
            dims=(2, 2))
probs:
[1. 0. 0. 0.]

We understand that the first element of Statevector is

∣ 00 ⟩

, and has probability of 1.0.

Next we take the state after a Hadamard gate on the first qubit:

h:
state:
Statevector([0.70710678+0.j, 0.70710678+0.j, 0.        +0.j,
             0.        +0.j],
            dims=(2, 2))
probs:
[0.5 0.5 0.  0. ]

We now understand that the second element of the Statevector is

∣ 01 ⟩

, and now we have a 50/50 propabability split for the first bit.

Then we apply the CNOT gate:

cx:
state:
Statevector([0.70710678+0.j, 0.        +0.j, 0.        +0.j,
             0.70710678+0.j],
            dims=(2, 2))
probs:
[0.5 0.  0.  0.5]

which leaves us with the final

\frac{∣ 0 0 ⟩ + ∣ 1 1 ⟩}{2}

.

Then we print the circuit a bit:

qc without measure:
     ┌───┐
q_0: ┤ H ├──■──
     └───┘┌─┴─┐
q_1: ─────┤ X ├
          └───┘
c: 2/══════════

qc with measure:
     ┌───┐     ┌─┐
q_0: ┤ H ├──■──┤M├───
     └───┘┌─┴─┐└╥┘┌─┐
q_1: ─────┤ X ├─╫─┤M├
          └───┘ ║ └╥┘
c: 2/═══════════╩══╩═
                0  1
qasm:
OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
h q[0];
cx q[0],q[1];
measure q[0] -> c[0];
measure q[1] -> c[1];

And finally we compile the circuit and do some sample measurements:

qct:
     ┌───┐     ┌─┐
q_0: ┤ H ├──■──┤M├───
     └───┘┌─┴─┐└╥┘┌─┐
q_1: ─────┤ X ├─╫─┤M├
          └───┘ ║ └╥┘
c: 2/═══════════╩══╩═
                0  1
counts={'11': 484, '00': 516}
counts={'11': 493, '00': 507}

 Read the full article

Introduction to quantum computing  Updated 2024-12-15  +Created 1970-01-01

 View more

Course plan:

Section "Programmer's model of quantum computers"
look at a Qiskit hello world
- e.g. ours: qiskit/hello.py
learn about quantum circuits.
- tensor product in quantum computing
- First we learn some quantum logic gates. This shows an alternative, and extremely important view of a quantum computer besides a matrix multiplication: as a circuit. Fundamental subsections:
- quantum algorithms
  - Section "Quantum Fourier transform"
  - Section "Shor's algorithm"

 Read the full article

Photonic quantum computer  Updated 2024-12-15  +Created 1970-01-01

 View more

Uses photons!

The key experiment/phenomena that sets the basis for photonic quantum computing is the two photon interference experiment.

The physical representation of the information encoding is very easy to understand:

input: we choose to put or not photons into certain wires or no
interaction: two wires pass very nearby at some point, and photons travelling on either of them can jump to the other one and interact with the other photons
output: the probabilities that photos photons will go out through one wire or another

Video 1.

Jeremy O'Brien: "Quantum Technologies" by GoogleTechTalks (2014)

Source. This is a good introduction to a photonic quantum computer. Highly recommended.

youtube.com/watch?v=7wCBkAQYBZA&t=1285 shows an experimental curve for a two photon interference experiment by Hong, Ou, Mandel (1987)
youtube.com/watch?v=7wCBkAQYBZA&t=1440 shows a KLM CNOT gate
youtube.com/watch?v=7wCBkAQYBZA&t=2831 discusses the quantum error correction scheme for photonic QC based on the idea of the "Raussendorf unit cell"

 Read the full article

qiskit/initialize.py  Updated 2024-12-15  +Created 1970-01-01

 View more

In this example we will initialize a quantum circuit with a single CNOT gate and see the output values.

By default, Qiskit initializes every qubit to 0 as shown in the qiskit/hello.py. But we can also initialize to arbitrary values as would be done when computing the output for various different inputs.

Output:

     ┌──────────────────────┐
q_0: ┤0                     ├──■──
     │  Initialize(1,0,0,0) │┌─┴─┐
q_1: ┤1                     ├┤ X ├
     └──────────────────────┘└───┘
c: 2/═════════════════════════════

init: [1, 0, 0, 0]
probs: [1. 0. 0. 0.]

init: [0, 1, 0, 0]
probs: [0. 0. 0. 1.]

init: [0, 0, 1, 0]
probs: [0. 0. 1. 0.]

init: [0, 0, 0, 1]
probs: [0. 1. 0. 0.]

     ┌──────────────────────────────────┐
q_0: ┤0                                 ├──■──
     │  Initialize(0.70711,0,0,0.70711) │┌─┴─┐
q_1: ┤1                                 ├┤ X ├
     └──────────────────────────────────┘└───┘
c: 2/═════════════════════════════════════════

init: [0.7071067811865475, 0, 0, 0.7071067811865475]
probs: [0.5 0.5 0.  0. ]

which we should all be able to understand intuitively given our understanding of the CNOT gate and quantum state vectors.

quantumcomputing.stackexchange.com/questions/13202/qiskit-initializing-n-qubits-with-binary-values-0s-and-1s describes how to initialize circuits qubits only with binary 0 or 1 to avoid dealing with the exponential number of elements of the quantum state vector.

 Read the full article

Quantum logic gates are needed for physical implementation  Updated 2024-12-15  +Created 1970-01-01

 View more

One direct practical reason is that we need to map the matrix to real quantum hardware somehow, and all quantum hardware designs so far and likely in the future are gate-based: you manipulate a small number of qubits at a time (2) and add more and more of such operations.

While there are "quantum compilers" to increase the portability of quantum programs, it is to be expected that programs manually crafted for a specific hardware will be more efficient just like in classic computers.

TODO: is there any clear reason why computers can't beat humans in approximating any unitary matrix with a gate set?

This is analogous to what classic circuit programmers will do, by using smaller logic gates to create complex circuits, rather than directly creating one huge truth table.

The most commonly considered quantum gates take 1, 2, or 3 qubits as input.

The gates themselves are just unitary matrices that operate on the input qubits and produce the same number of output qubits.

For example, the matrix for the CNOT gate, which takes 2 qubits as input is:

The final question is then: if I have a 2 qubit gate but an input with more qubits, say 3 qubits, then what does the 2 qubit gate (4x4 matrix) do for the final big 3 qubit matrix (8x8)? In order words, how do we scale quantum gates up to match the total number of qubits?

The intuitive answer is simple: we "just" extend the small matrix with a larger identity matrix so that the sum of the probabilities third bit is unaffected.

More precisely, we likely have to extend the matrix in a way such that the partial measurement of the original small gate qubits leaves all other qubits unaffected.

For example, if the circuit were made up of a CNOT gate operating on the first and second qubits as in:

0 ----+----- 0
      |
1 ---CNOT--- 1

2 ---------- 2

then we would just extend the 2x2 CNOT gate to:

TODO lazy to properly learn right now. Apparently you have to use the Kronecker product by the identity matrix. Also, zX-calculus appears to provide a powerful alternative method in some/all cases.

Bibliography:

quantumcomputing.stackexchange.com/questions/2299/how-to-interpret-a-quantum-circuit-as-a-matrix

 Read the full article

Tensor product in quantum computing  Updated 2024-12-15  +Created 1970-01-01

 View more

We don't need to understand a super generalized version of tensor products to know what they mean in basic quantum computing!

Intuitively, taking a tensor product of two qubits simply means putting them together on the same quantum system/computer.

When we write the bra-ket notation:

∣ 00 ⟩

that is the same as

∣ 0 ⟩ \otimes ∣ 0 ⟩

.

The tensor product is called a "product" because it distributes over addition.

E.g. consider:

(\frac{∣ 0 ⟩ + ∣ 1 ⟩}{2}) \otimes ∣ 0 ⟩ = \frac{∣ 0 ⟩ \otimes ∣ 0 ⟩ + ∣ 1 ⟩ \otimes ∣ 0 ⟩}{2} = \frac{∣ 0 0 ⟩ + ∣ 1 0 ⟩}{2}

(1)

Intuitively, in this operation we just put a Hadamard gate qubit together with a second pure

∣ 0 ⟩

qubit.

And the outcome still has the second qubit as always 0, because we haven't made them interact.

The quantum state

\frac{∣ 0 0 ⟩ + ∣ 1 0 ⟩}{2}

is called a separable state, because it can be written as a single product of two different qubits. We have simply brought two qubits together, without making them interact.

If we then add a CNOT gate to make a Bell state:

\frac{∣ 0 0 ⟩ + ∣ 1 1 ⟩}{2} = \frac{∣ 0 ⟩ \otimes ∣ 0 ⟩ + ∣ 1 ⟩ \otimes ∣ 1 ⟩}{2}

(2)

we can now see that the Bell state is non-separable: we've made the two qubits interact, and there is no way to write this state with a single tensor product. The qubits are fundamentally entangled.

 Read the full article

Ciro Santilli @cirosantilli 34

 Incoming links: CNOT gate