Incoming links: Energy
The neutron temperature example is crucial: you just can't give the cross section of a target alone, the energy of the incoming beam also matters.
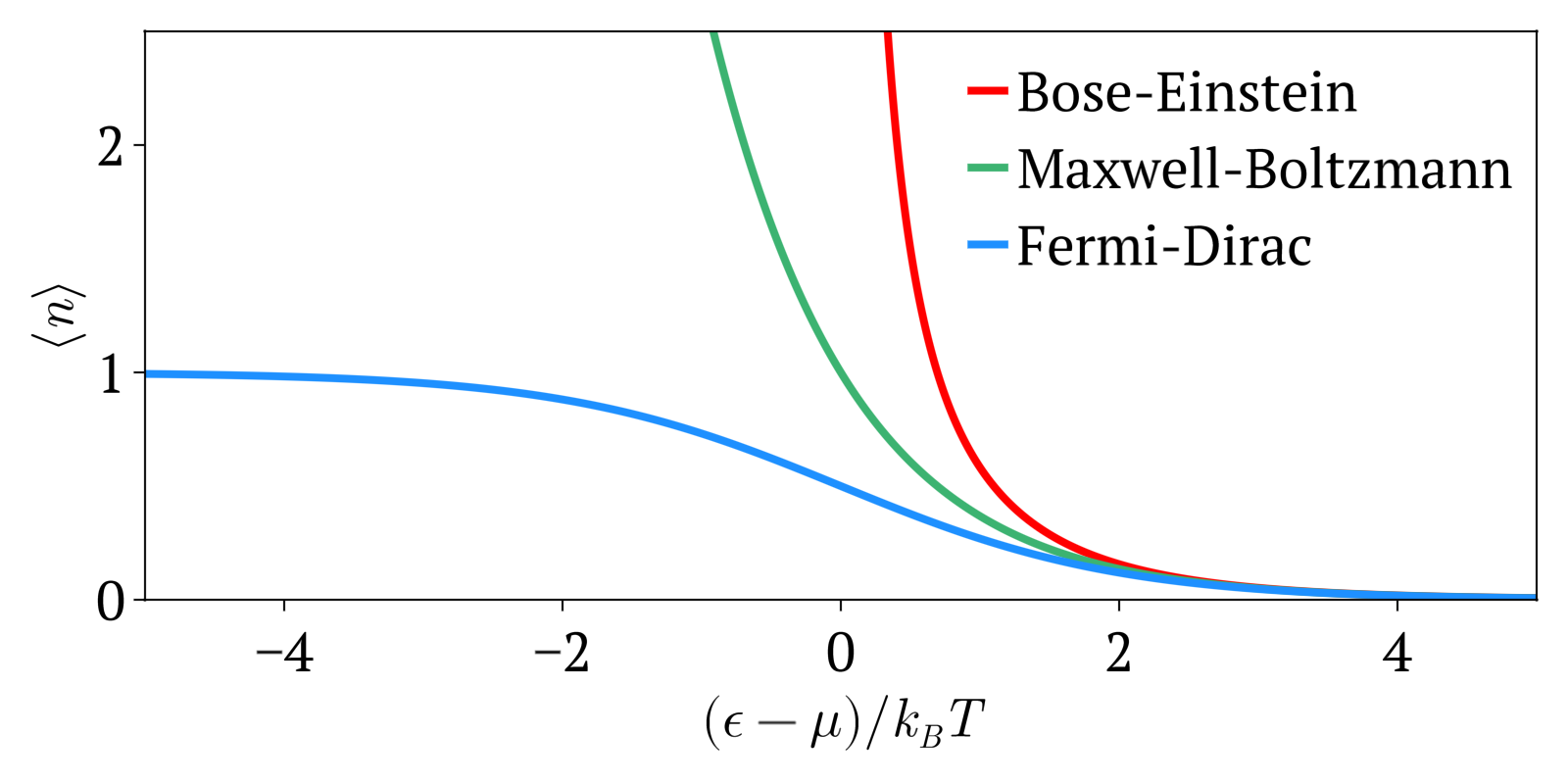
Maxwell-Boltzmann vs Bose-Einstein vs Fermi-Dirac statistics Updated 2024-12-15 +Created 2024-10-28
Maxwell-Boltzmann statistics, Bose-Einstein statistics and Fermi-Dirac statistics all describe how energy is distributed in different physical systems at a given temperature.
For example, Maxwell-Boltzmann statistics describes how the speeds of particles are distributed in an ideal gas.
The temperature of a gas is only a statistical average of the total energy of the gas. But at a given temperature, not all particles have the exact same speed as the average: some are higher and others lower than the average.
For a large number of particles however, the fraction of particles that will have a given speed at a given temperature is highly deterministic, and it is this that the distributions determine.
One of the main interest of learning those statistics is determining the probability, and therefore average speed, at which some event that requires a minimum energy to happen happens. For example, for a chemical reaction to happen, both input molecules need a certain speed to overcome the potential barrier of the reaction. Therefore, if we know how many particles have energy above some threshold, then we can estimate the speed of the reaction at a given temperature.
The three distributions can be summarized as:
- Maxwell-Boltzmann statistics: statistics without considering quantum statistics. It is therefore only an approximation. The other two statistics are the more precise quantum versions of Maxwell-Boltzmann and tend to it at high temperatures or low concentration. Therefore this one works well at high temperatures or low concentrations.
- Bose-Einstein statistics: quantum version of Maxwell-Boltzmann statistics for bosons
- Fermi-Dirac statistics: quantum version of Maxwell-Boltzmann statistics for fermions. Sample system: electrons in a metal, which creates the free electron model. Compared to Maxwell-Boltzmann statistics, this explained many important experimental observations such as the specific heat capacity of metals. A very cool and concrete example can be seen at youtu.be/5V8VCFkAd0A?t=1187 from Video "Using a Photomultiplier to Detect single photons by Huygens Optics" where spontaneous field electron emission would follow Fermi-Dirac statistics. In this case, the electrons with enough energy are undesired and a source of noise in the experiment.
Maxwell-Boltzmann vs Bose-Einstein vs Fermi-Dirac statistics
. Source. 
A good conceptual starting point is to like the example that is mentioned at The Harvest of a Century by Siegmund Brandt (2008).
Consider a system with 2 particles and 3 states. Remember that:
- in quantum statistics (Bose-Einstein statistics and Fermi-Dirac statistics), particles are indistinguishable, therefore, we might was well call both of them
A, as opposed toAandBfrom non-quantum statistics - in Bose-Einstein statistics, two particles may occupy the same state. In Fermi-Dirac statistics
Therefore, all the possible way to put those two particles in three states are for:
- Maxwell-Boltzmann distribution: both A and B can go anywhere:
State 1 State 2 State 3 AB AB AB A B B A A B B A A B B A - Bose-Einstein statistics: because A and B are indistinguishable, there is now only 1 possibility for the states where A and B would be in different states.
State 1 State 2 State 3 AA AA AA A A A A A A - Fermi-Dirac statistics: now states with two particles in the same state are not possible anymore:
State 1 State 2 State 3 A A A A A A
Used to explain the black-body radiation experiment.
Published as: On the Theory of the Energy Distribution Law of the Normal Spectrum by Max Planck (1900).
The Quantum Story by Jim Baggott (2011) page 9 mentions that Planck apparently immediately recognized that Planck constant was a new fundamental physical constant, and could have potential applications in the definition of the system of units (TODO where was that published):This was a visionary insight, and was finally realized in the 2019 redefinition of the SI base units.
Planck wrote that the constants offered: 'the possibility of establishing units of length, mass, time and temperature which are independent of specific bodies or materials and which necessarily maintain their meaning for all time and for all civilizations, even those which are extraterrestrial and nonhuman, constants which therefore can be called "fundamental physical units of measurement".'
TODO how can it be derived from theoretical principles alone? There is one derivation at; en.wikipedia.org/wiki/Planck%27s_law#Derivation but it does not seem to mention the Schrödinger equation at all.
Quantum Mechanics 2 - Photons by ViaScience (2012)
Source. Contains a good explanation of how discretization + energy increases with frequency explains the black-body radiation experiment curve: you need more and more energy for small wavelengths, each time higher above the average energy available.In this solution of the Schrödinger equation, by the uncertainty principle, position is completely unknown (the particle could be anywhere in space), and momentum (and therefore, energy) is perfectly known.
The plane wave function appears for example in the solution of the Schrödinger equation for a free one dimensional particle. This makes sense, because when solving with the time-independent Schrödinger equation, we do separation of variable on fixed energy levels explicitly, and the plane wave solutions are exactly fixed energy level ones.
Analects translation by Robert Eno (2015) 16.7: