This is what happens when you apply a DC voltage across a Josephson junction.
It is called "AC effect" because when we apply a DC voltage, it produces an alternating current on the device.
By looking at the Josephson equations, we see that a positive constant, then just increases linearly without bound.
Therefore, from the first equation:we see that the current will just vary sinusoidally between .
This meas that we can use a Josephson junction as a perfect voltage to frequency converter.
Wikipedia mentions that this frequency is , so it is very very high, so we are not able to view individual points of the sine curve separately with our instruments.
Also it is likely not going to be very useful for many practical applications in this mode.
An I-V curve can also be seen at: Figure "Electron microscope image of a Josephson junction its I-V curve".
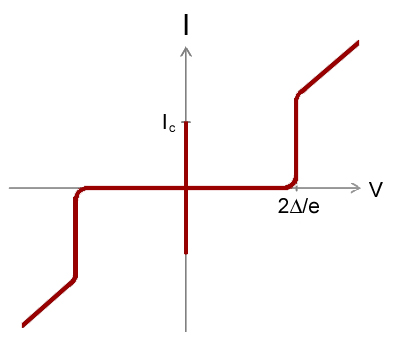
I-V curve of the AC Josephson effect
. Source. 
Voltage is horizontal, current vertical. The vertical bar in the middle is the effect of interest: the current is going up and down very quickly between , the Josephson current of the device. Because it is too quick for the oscilloscope, we just see a solid vertical bar.
The non vertical curves at right and left are just other effects we are not interested in.
TODO what does it mean that there is no line at all near the central vertical line? What happens at those voltages?
Superconducting Transition of Josephson junction by Christina Wicker (2016)
Source. Amazing video that presumably shows the screen of a digital oscilloscope doing a voltage sweep as temperature is reduced and superconductivity is reached.
Articles by others on the same topic
There are currently no matching articles.