Josephson effect (1962)

Discrete quantum effect observed in superconductors with a small insulating layer, a device known as a Josephson junction.

To understand the behaviour effect, it is important to look at the Josephson equations consider the following Josephson effect regimes separately:

A good summary from Wikipedia by physicist Andrew Whitaker:

at a junction of two superconductors, a current will flow even if there is no drop in voltage; that when there is a voltage drop, the current should oscillate at a frequency related to the drop in voltage; and that there is a dependence on any magnetic field

Bibliography:

www.youtube.com/watch?v=cnZ6exn2CkE "Superconductivity: Professor Brian Josephson". Several random excerpts from Cambridge people talking about the Josephson effect

Table of contents

History of the Josephson effect

0 0

In 1962 Brian Josephson published his inaugural paper predicting the effect as Section "Possible new effects in superconductive tunnelling (1963, Prediction of the Josephson effect)".

In 1963 Philip W. Anderson and John M. Rowell published their paper that first observed the effect as Section "Possible new effects in superconductive tunnelling (1963, Prediction of the Josephson effect)".

Some golden notes can be found at True Genius: The Life and Science of John Bardeen page 224 and around. Philip W. Anderson commented:

We were all - Josephson, Pippard and myself, as well as various other people who also habitually sat at the Mond tea and participated in the discussions of the next few weeks - very much puzzled by the meaning of the fact that the current depends on the phase

As part of the course Anderson had introduced the concept of broken symmetry in superconductors. Josephson "was fascinated by the idea of broken symmetry, and wondered whether there could be any way of observing it experimentally."

Possible new effects in superconductive tunnelling (1963, Prediction of the Josephson effect)

0 0

The inaugural that predicted the Josephson effect.

Published on Physics Letters, then a new journal, before they split into Physics Letters A and Physics Letters B. True Genius: The Life and Science of John Bardeen mentions that this choice was made rather than the more prestigious Physical Review Letters because they were not yet so confident about the results.

Paywalled by Elsevier as of 2023 at: www.sciencedirect.com/science/article/abs/pii/0031916362913690

Probable observation of the Josephson superconducting tunneling effect (1963, Observation of the Josephson effect)

0 0

Paper by Philip W. Anderson and John M. Rowell that first (?) experimentally observed the Josephson effect.

Paywalled by the American Physical Society as of 2023 at: journals.aps.org/prl/abstract/10.1103/PhysRevLett.10.230

DOI: doi.org/10.1103/PhysRevLett.10.230

TODO understand the graphs in detail.

They used tin-oxide-lead tunnel at 1.5 K. TODO oxide of what? Why two different metals? They say that both films are 200 nm thick, so maybe it is:

   -----+------+------+-----
...  Sn | SnO2 | PbO2 | Pb  ...
   -----+------+------------
          100nm 100nm

A reconstruction of their circuit in Ciro's ASCII art circuit diagram notation TODO:

DC---R_10---X---G

There are not details of the physical construction of course. Reproducibility lol.

Figure 1.
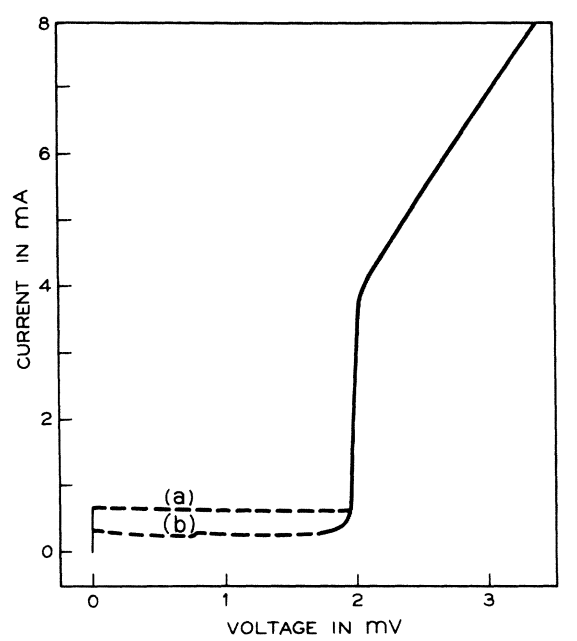
Figure 1 of Probable observation of the Josephson superconducting tunneling effect
. TODO what do the dotted lines mean?

Figure 2.
Figure 2 of Probable observation of the Josephson superconducting tunneling effect
.

Josephson effect regime

0 0

DC Josephson effect

0 0

AC Josephson effect

0 0

This is what happens when you apply a DC voltage across a Josephson junction.

It is called "AC effect" because when we apply a DC voltage, it produces an alternating current on the device.

By looking at the Josephson equations, we see that

V (t) = k

a positive constant, then

φ

just increases linearly without bound.

Therefore, from the first equation:

I (t) = I_{c} sin (φ (t))

(1)

we see that the current will just vary sinusoidally between

\pm I_{c}

This meas that we can use a Josephson junction as a perfect voltage to frequency converter.

Wikipedia mentions that this frequency is

484 G H z / m V

, so it is very very high, so we are not able to view individual points of the sine curve separately with our instruments.

Also it is likely not going to be very useful for many practical applications in this mode.

An I-V curve can also be seen at: Figure "Electron microscope image of a Josephson junction its I-V curve".

Figure 1.
I-V curve of the AC Josephson effect
. Source.
Voltage is horizontal, current vertical. The vertical bar in the middle is the effect of interest: the current is going up and down very quickly between $\pm I_{c}$ , the Josephson current of the device. Because it is too quick for the oscilloscope, we just see a solid vertical bar.
The non vertical curves at right and left are just other effects we are not interested in.
TODO what does it mean that there is no line at all near the central vertical line? What happens at those voltages?

Video 1.

Superconducting Transition of Josephson junction by Christina Wicker (2016)

Source. Amazing video that presumably shows the screen of a digital oscilloscope doing a voltage sweep as temperature is reduced and superconductivity is reached.

Figure 2.
I-V curve of a superconducting tunnel junction
. So it appears that there is a zero current between $V = 0$ and $V = 2 Δ / e$ . Why doesn't it show up on the oscilloscope sweeps, e.g. Video 1. "Superconducting Transition of Josephson junction by Christina Wicker (2016)"?

Inverse AC Josephson effect

0 0

If you shine microwave radiation on a Josephson junction, it produces a fixed average voltage that depends only on the frequency of the microwave. TODO how is that done more preciesely? How to you produce and inject microwaves into the thing?

It acts therefore as a perfect frequency to voltage converter.

The Wiki page gives the formula: en.wikipedia.org/wiki/Josephson_effect#The_inverse_AC_Josephson_effect You get several sinusoidal harmonics, so the output is not a perfect sine. But the infinite sum of the harmonics has a fixed average voltage value.

And en.wikipedia.org/wiki/Josephson_voltage_standard#Josephson_effect mentions that the effect is independent of the junction material, physical dimension or temperature.

All of the above, compounded with the fact that we are able to generate microwaves with extremely precise frequency with an atomic clock, makes this phenomenon perfect as a Volt standard, the Josephson voltage standard.

TODO understand how/why it works better.

Shapiro steps

0 0

Josephson equations

0 0

Two equations derived from first principles by Brian Josephson that characterize the device, somewhat like an I-V curve:

I (t) = I_{c} sin (φ (t)) \frac{d φ ( t )}{d t} = \frac{2 e V ( t )}{ℏ}

(1)

where:

$I_{c}$ : Josephson current
$φ$ : the Josephson phase, a function $R \to R$ defined by the second equation plus initial conditions
$V (t)$ : input voltage of the system
$I (t)$ : current across the junction, determined by the input voltage

Note how these equations are not a typical I-V curve, as they are not an instantaneous dependency between voltage and current: the history of the voltage matters! Or in other words, the system has an internal state, represented by the Josephson phase at a given point in time.

To understand them better, it is important to look at some important cases separately:

AC Josephson effect: V is a fixed DC voltage

Josephson current ( $I_{c}$ )

0 0

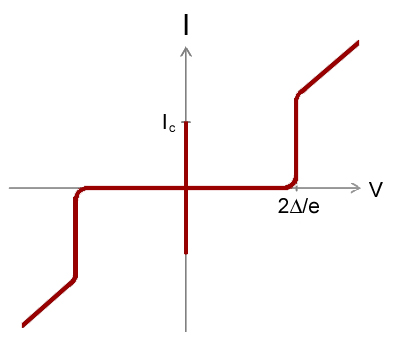
Maximum current that can flow across a Josephson junction, as can be directly seen from the Josephson equations.

Is a fixed characteristic value of the physical construction of the junction.

Josephson phase ( $φ$ )

0 0

A function

R \to R

defined by the second of the Josephson equations plus initial conditions.

It represents an internal state of the junction.

Josephson junction

0 0

A device that exhibits the Josephson effect.

Figure 1.
Electron microscope image of a Josephson junction its I-V curve
. Source.

Pi Josephson junction

1 0

Magnetic flux quantum

1 0

TODO is there any relationship between this and the Josephson effect?

Experimental observation published as Experimental Evidence for Quantized Flux in Superconducting Cylinders.

This appears to happen to any superconducting loop, because the superconducting wave function has to be continuous.

Video "Superconducting Qubit by NTT SCL (2015)" suggests that anything in between gets cancelled out by a superposition of current in both directions.

Experimental Evidence for Quantized Flux in Superconducting Cylinders (1961, Bascom S. Deaver, Jr., William M. Fairbank)

0 0

Paywalled at: journals.aps.org/prl/abstract/10.1103/PhysRevLett.7.43

The first published experimental observation of the magnetic flux quantum.

The paper that follows it in the journal is also of interest, "Theoretical Considerations Concerning Quantized Magnetic Flux In Superconducting Cylinders" by N. Byers and C. N. Yang, it starts:

In a recent experiment, the magnetic flux through a superconducting ring has been found to be quantized in units of ch/2e. Quantization in twice this unit has been briefly discussed by London' and by Onsager. ' Onsager' has also considered the possibility of quantization in units ch/2e due to pairs of electrons forming quasi-bosons.

So there was some previous confusion about the flux quantum due to the presence of Cooper pairs or not.

Dumping the fitures at: archive.org/details/experimental-evidence-for-quantized-flux-in-superconducting-cylinders One day we can also dump the paper scans when it goes into the public domain in 2056! Public domain scientific paper by year.

Figure 1.
Figure 1 of Experimental Evidence for Quantized Flux in Superconducting Cylinders
. The legend reads:
(Upper) Trapped flux in cylinder No. 1 as a function of magnetic field in which the cylinder was cooled below the superconducting transition. temperature. The open circles are individual data points. The solid circles represent th, e average value of all data points at a particular value of applied field including all the points plotted and additional data which could not be plotted due to severe overlapping of points. Approximately two hundred data points are represented. The lines are drawn at multiples of hc/2e.
(Lower) Net flux in cylinder No. 1 before turning off the applied field in which it was cooled as a function of the applied field. Open and solid circles have the same significance as above. The lower line is the diamagnetic calibration to which all runs have been normalized. The other lines are translated vertically by successive steps of hc/2e.

Figure 2.
Figure 2 of Experimental Evidence for Quantized Flux in Superconducting Cylinders
. The legend reads:
(Upper) Trapped flux in cylinder No. 2 as a function of magnetic field in which the cylinder was cooled below the superconducting transition temperature. The circles and triangles indicate points for oppositely directed applied fields. Lines are drawn at multiples of hc/2e.
(Lower) Net flux in cylinder No. 2 before turning off the applied field as a function of the applied field. The circles and triangles are points for oppositely directed applied fields. The lower line is the diamagnetic calibration to which all runs have The other been normalized. lines are translated vertically by successive steps of hc/2e.

Josephson constant

0 0

The inverse of the magnetic flux quantum.

Symmetry breaking in superconductors

0 0

physics.stackexchange.com/questions/133780/superconductor-symmetry-breaking

As mentioned in True Genius: The Life and Science of John Bardeen page 224, the idea of symmetry breaking was a major motivation in Josephson's study of the Josephson effect.

Applications of Josephson Junctions

0 0

the basis for the most promising 2019 quantum computing implementation: superconducting quantum computer
Josephson voltage standard: the most practical/precise Volt standard, which motivated the definition of the ampere in the 2019 redefinition of the SI base units
SQUID devices, which are:
- very precise magnetometer
- the basis for superconducting quantum computers

Josephson voltage standard (JVS)

1 0

The most practical/precise volt standard.

It motivated the definition of the ampere in the 2019 redefinition of the SI base units

Quick NIST article about it: www.nist.gov/news-events/news/2013/04/primary-voltage-standard-whole-world (archive)

The wiki page en.wikipedia.org/wiki/Josephson_voltage_standard contains amazing schematics of the device, apparently made by the US Government.

Video 1.

The evolution of voltage metrology to the latest generation of JVSs by Alain Rüfenacht

. Source. Talk given in 2023. The speaker is from NIST, and the talk was hosted by the BIPM. Fantastic talk.

Video 2.

Technical aspects of realizing the DC volt in the laboratory with a JVS by Stéphane Solve

. Source. Talk given in 2023. The speaker is from BIPM, and the talk was hosted by the BIPM. Fantastic talk.

SQUID device

0 0

Can be used as a very precise magnetometer.

There are high temperature yttrium barium copper oxide ones that work on liquid nitrogen.

Video 1.

Superconducting Quantum Interference Device by Felipe Contipelli (2019)

Source. Good intuiotionistic video. Some points deserved a bit more detail.

Video 2.

Mishmash of SQUID interviews and talks by Bartek Glowaki

. Source.

The videos come from: www.ascg.msm.cam.ac.uk/lectures/. Vintage.

Mentions that the SQUID device is analogous to a double-slit experiment.

One of the segments is by John Clarke.

Video 3.

Superconducting Quantum Interference Devices by UNSW Physics (2020)

Source.

An experimental lab video for COVID-19 lockdown. Thanks, COVID-19. Presented by a cute and awkward Adam Stewart.

Uses a SQUID device and control system made by STAR Cryoelectronics. We can see Mr. SQUID EB-03 written on the probe and control box, that is their educational product.

As mentioned on the Mr. SQUID specs, it is a high-temperature superconductor, so liquid nitrogen is used.

He then measures the I-V curve on an Agilent Technologies oscilloscope.

Unfortunately, the video doesn't explain very well what is happening behind the scenes, e.g. with a circuit diagram. That is the curse of university laboratory videos: some of them assume that students will have material from other internal sources.

youtu.be/ql2Yo5LgU8M?t=211 shows the classic voltage oscillations, presumably on a magnetic field sweep, and then he puts a magnet next to the device from outside the Dewar
youtu.be/ql2Yo5LgU8M?t=253 demonstrates the formation of Shapiro steps. Inserts a Rohde & Schwarz signal generator into the Dewar to vary the flux. The result is not amazing, but they are visible somewhat.