Oxford Master Course in Mathematical and Theoretical Physics Updated 2025-07-16
Three polarizers 45 degrees apart Updated 2025-07-16
Kilogram Updated 2025-07-16
Unit of mass.
Defined in the 2019 redefinition of the SI base units via the Planck constant. This was possible due to the development of the Kibble balance.
NuNET Updated 2025-07-16
SQL
COUNT function Updated 2025-07-16Have a look at some interesting examples under nodejs/sequelize/raw/many_to_many.js.
University of Cambridge student culture Updated 2025-07-16
Ciro Santilli's ancestors Updated 2025-07-16
Where most of Ciro Santilli's ancestors came from, and why Ciro has the Italian nationality as well as Brazilian.
More specifically his paternal line comes from Gissi in the Abruzzo region.
Ciro feels really bad by the fact that he does not speak Italian and has never visited Gissi as of 2020.
He would likely be able to learn Italian in like 3 months because it is so similar to Portuguese and French which he already speaks.
And a cycling visit maybe? That would be amazing! en.wikipedia.org/wiki/Giro_d'Abruzzo | www.youtube.com/watch?v=OW7wqa3vNU8&list=UU35qUU5iZPvuzcre43EV8bA&index=25
For what it is worth though, Ciro Santilli does honestly love Europe, and feels a strong desire to make it even awesomer, along with the rest of the world. Despite this being a hopeless attempt due to having more than one natural language is bad for the world.
Particle decay Updated 2025-07-16
Can produce two entangled particles.
Relativistic particle in a box thought experiment Updated 2025-07-16
Described for example in lecture 1.
SQL
genenerate_series Updated 2025-07-16 SQL transaction isolation level Updated 2025-07-16
Each transaction isolation level specifies what can or cannot happen when two queries are being run in parallel, i.e.: the memory semantics of the system.
Remember that queries can affects thousands of rows, and database systems like PostgreSQL can run multiple such queries at the same time.
Implementation specifics:
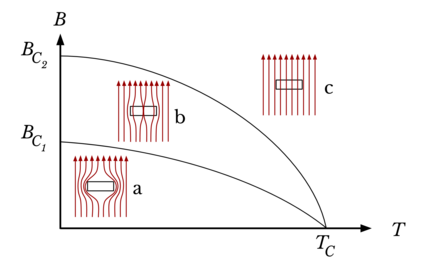
Type-II superconductor Updated 2025-07-16
Charlie Wilson's War Updated 2025-07-16
Agilent Technologies oscilloscope Updated 2025-07-16
Ciro Santilli's bad old event memory Updated 2025-07-16
Ciro Santilli has a bad memory for events that happened a medium time ago, for example in order of months/years. Especially if they are one-off things that have no relation to anything else.
For example, Ciro never remembers which places he travelled to just once, and who was in each trip! He has images of several places he travelled to in his head, and would recognize them, but he just doesn't know where they were!
Another example, Ciro was looking at the carpet at their house, and asked where it came from. His wife replied immeidately: from Bercy shopping quarter in Paris about 10 years ago, and you took it on your back for a long walk until we could find the bus back home because we were concerned it wouldn't fit in the train!
The same goes for scenes from movies and passages from music, which explains why Ciro's art consumption focuses on innovative discrete "what happened" and "general gist" ideas, rather than, analog details such as colors and shapes.
Going back even further in time, Ciro starts to forget the less close friends he had, because the events start to fade away.
Paradoxically however, Ciro believes that this bad memory is one of his greatest strengths and key defining characteristics, because it leads Ciro to want to write down every interesting thing he learns, which motivated OurBigBook.com and his Stack Overflow contributions and his related Ciro Santilli's documentation superpowers.
It also somewhat leads Ciro to like physics and mathematics, because in these fields you "can deduce everything" from very few base principles, so if you forget them, it does not matter that much as you can re-deduce stuff over and over. Which is somewhat where the high flying bird attitude comes from. It is hard to go deep when you have to re-prove everything every time. But the upside is that anything that sticks, does so because it has a broad net to stick to, and therefore allows Ciro to make unusual and unexpected connections that others might not.
Ciro believes that there are two types of people, and most notably software engineers, which are basically data wranglers: those with bad memory and those with good memory.
Those with bad memory, tend to focus on automating and improving their processes a lot. They take much longer to do one-off specific deep knowledge tasks however.
The downside of the good memory ones is that sooner or later they will find tasks that no matter how much memory they have, they cannot solve without automation, and they will fail at those.
This dichotomy also explains why Ciro sucks at code reviews, but is rather the person who runs the interesting patches by himself and finds some critical problems that the more theoretical code reviewers missed.
If Ciro had become a scientist, he would without doubt be an experimentalist, just like in this reality he is a GDB/runtime person rather than a "static source analysis" person. Those who have bad memory prefer to just run experiments over and over and observe system state at runtime.
Other effects of having a bad memory include:
- code duplication, or a constant fear of it at least, because Ciro forgets that some functionality exists already
- meeting aversion, because everything that is not recorded will fade away
- passion for backward design, because by the time a piece of knowledge learnt in school might be useful (and 99.99% won't), it will have been long forgotten
Related: jakobschwichtenberg.com/about/ from Jakob Schwichtenberg:
In some sense, one of the biggest benefits I have over other people in physics is that I'm certainly not the smartest guy! I usually can't grasp complex issues very easily. So I have to break down complex ideas into smaller chunks to understand it myself. This means, whenever I describe something to others, everyone understands, because it's broken down into such simple terms.
On C2 wiki, therefore it cannot be wrong wiki.c2.com/?QuasiGreatTeacher:
Closure table Updated 2025-07-16
Krusader Updated 2025-07-16
The most powerful GUI file manager ever?? Infinite configurability??
Ciro Santilli wasted some time on it before he gave up on file managers altogether and started using only the CLI with a few aliases.
Lagrange's four-square theorem Updated 2025-07-16
x86 Paging Tutorial ARM Updated 2025-07-16
Information about ARM paging can be found at: cirosantilli.com/linux-kernel-module-cheat#arm-paging
x86 Paging Tutorial Basic TLB operation Updated 2025-07-16
After a translation between linear and physical address happens, it is stored on the TLB. For example, a 4 entry TLB starts in the following state:
valid linear physical
----- ------ --------
> 0 00000 00000
0 00000 00000
0 00000 00000
0 00000 00000The
> indicates the current entry to be replaced.And after a page linear address and after a second translation of
00003 is translated to a physical address 00005, the TLB becomes: valid linear physical
----- ------ --------
1 00003 00005
> 0 00000 00000
0 00000 00000
0 00000 0000000007 to 00009 it becomes: valid linear physical
----- ------ --------
1 00003 00005
1 00007 00009
> 0 00000 00000
0 00000 00000 Unlisted articles are being shown, click here to show only listed articles.