Ciro Santilli @cirosantilli 35

Theory that atoms exist, i.e. matter is not continuous.

Much before atoms were thought to be "experimentally real", chemists from the 19th century already used "conceptual atoms" as units for the proportions observed in macroscopic chemical reactions, e.g. $2H_2+O_2\leftrightarrow H_{2}O$. The thing is, there was still the possibility that those proportions were made up of something continuous that for some reason could only combine in the given proportions, so the atoms could only be strictly consider calculatory devices pending further evidence.

Subtle is the Lord by Abraham Pais (1982) chapter 5 "The reality of molecules" has some good mentions. Notably, physicists generally came to believe in atoms earlier than chemists, because the phenomena they were most interested in, e.g. pressure in the ideal gas law, and then Maxwell-Boltzmann statistics just scream atoms more loudly than chemical reactions, as they saw that these phenomena could be explained to some degree by traditional mechanics of little balls.

Confusion around the probabilistic nature of the second law of thermodynamics was also used as a physical counterargument by some. Pais mentions that Wilhelm Ostwald notably argued that the time reversibility of classical mechanics + the second law being a fundamental law of physics (and not just probabilistic, which is the correct hypothesis as we now understand) must imply that atoms are not classic billiard balls, otherwise the second law could be broken.

Pais also mentions that a big "chemical" breakthrough was isomers suggest that atoms exist.

Very direct evidence evidence:

Less direct evidence:

Subtle is the Lord by Abraham Pais (1982) page 40 mentions several methods that Einstein used to "prove" that atoms were real. Perhaps the greatest argument of all is that several unrelated methods give the same estimates of atom size/mass:

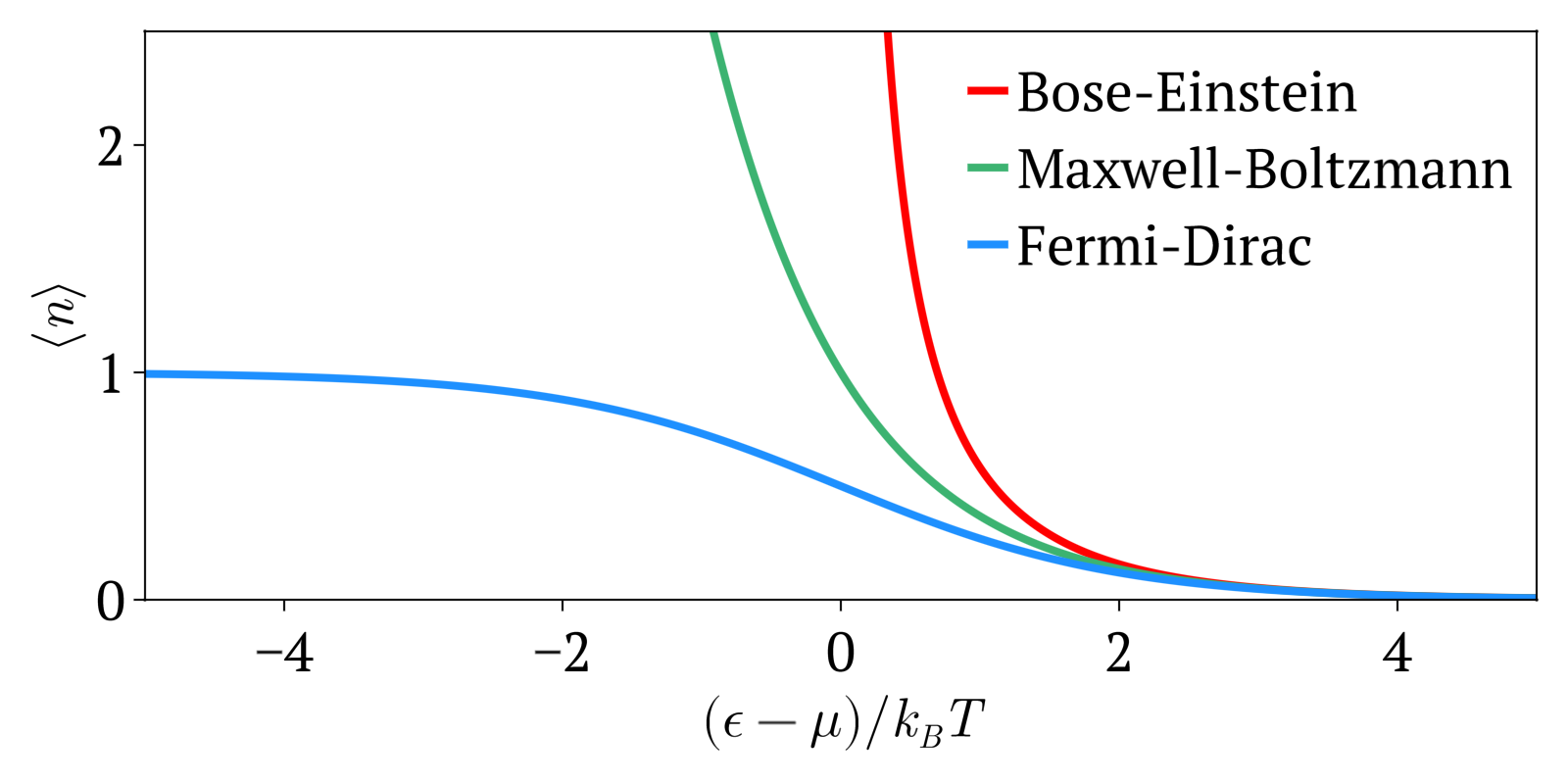
Maxwell-Boltzmann statistics, Bose-Einstein statistics and Fermi-Dirac statistics all describe how energy is distributed in different physical systems at a given temperature.

For example, Maxwell-Boltzmann statistics describes how the speeds of particles are distributed in an ideal gas.

The temperature of a gas is only a statistical average of the total energy of the gas. But at a given temperature, not all particles have the exact same speed as the average: some are higher and others lower than the average.

For a large number of particles however, the fraction of particles that will have a given speed at a given temperature is highly deterministic, and it is this that the distributions determine.

One of the main interest of learning those statistics is determining the probability, and therefore average speed, at which some event that requires a minimum energy to happen happens. For example, for a chemical reaction to happen, both input molecules need a certain speed to overcome the potential barrier of the reaction. Therefore, if we know how many particles have energy above some threshold, then we can estimate the speed of the reaction at a given temperature.

The three distributions can be summarized as:

A good conceptual starting point is to like the example that is mentioned at The Harvest of a Century by Siegmund Brandt (2008).

Consider a system with 2 particles and 3 states. Remember that:

Therefore, all the possible way to put those two particles in three states are for: