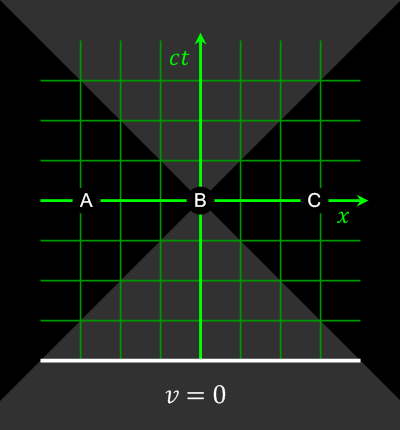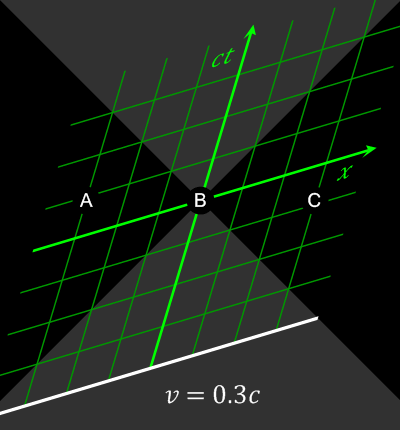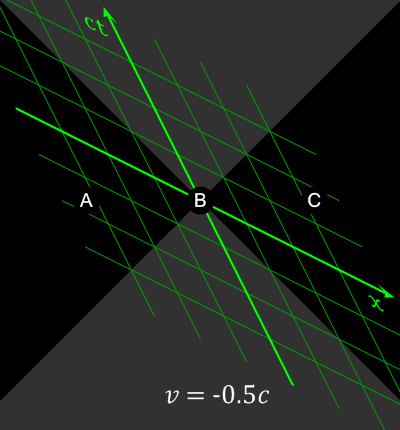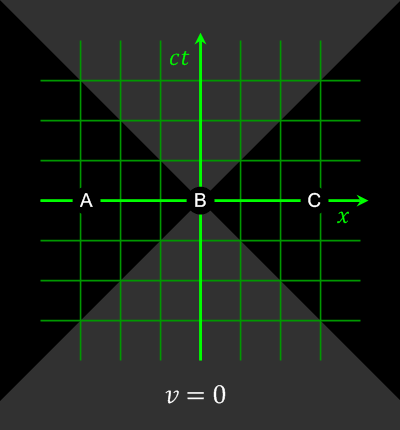
A 4D gradient with some small special relativity specifics added in (the light of speed and sign change for the time).

Minkowski space

R^{4}

with a weird dot product-like operation called the Minkowski inner product.

The name given to this type of space is a pseudometric space.

Minkowski inner product

This form is not really an inner product in the common modern definition, because it is not positive definite, only a symmetric bilinear form.

By default, we will use the time negative representation unless stated otherwise:

η_{μ ν} = ⎣ ⎢ ⎢ ⎢ ⎡ - 1 000 010000100001 ⎦ ⎥ ⎥ ⎥ ⎤

but another equivalent one is to use a time positive representation:

η_{μ ν} = ⎣ ⎢ ⎢ ⎢ ⎡ 1000 0 - 1 00 00 - 1 0 000 - 1 ⎦ ⎥ ⎥ ⎥ ⎤

The matrix is typically denoted by the Greek letter eta.

Why should I care when I can calculate new x and new time with Lorentz transformation?

Answer: it can give some qualitative intuition on what is larger/smaller happens before/after based only on arguably more intuitive geometric considerations, without requiring you to do any calculations, see e.g. Figure "Spacetime diagram illustrating how faster-than-light travel implies time travel".

The key insights that it gives are:

future and past are well defined: every reference frame sees your future in your future cone, and your past in your past cone
Otherwise causality could be violated, and then things would go really bad, you could tell your past self to tell your past self to tell your past self to do something.
You can only affect the outcome of events in your future cone, and you can only be affected by events in your past cone. You can't travel fast enough to affect.
Two spacetime events with such fixed causality are called timelike-separated events.
every other event (to right and left, known as spacelike-separated events) can be measured to happen before or after your current spacetime event by different observers.
But that does not violate causality, because you just can't reach those spacetime points anyways to affect them.

Mathematically, we can decide if two events are timelike-separated or spacelike-separated by just looking at the sign of the spacetime interval between them.

On the light cone, these are events on the left/right part of the cone.

Different observers might not agree on the order of two spacelike-separated events.

Further discussion at Section "Light cone".

The opposite of those events are timelike-separated events.