Particle physics

Unified all previous electro-magnetism theories into one equation.

Explains the propagation of light as a wave, and matches the previously known relationship between the speed of light and electromagnetic constants.

The equations are a limit case of the more complete quantum electrodynamics, and unlike that more general theory account for the quantization of photon.

The equations are a system of partial differential equation.

The system consists of 6 unknown functions that map 4 variables: time t and the x, y and z positions in space, to a real number:

$E_{x} (t, x, y, z)$ , $E_{y} (t, x, y, z)$ , $E_{z} (t, x, y, z)$ : directions of the electric field $E : R^{4} \to R^{3}$
$B_{x} (t, x, y, z)$ , $B_{y} (t, x, y, z)$ , $B_{z} (t, x, y, z)$ : directions of the magnetic field $B : R^{4} \to R^{3}$

and two known input functions:

$ρ : R^{3} t o R$ : density of charges in space
$J : R^{3} \to R^{3}$ : current vector in space. This represents the strength of moving charges in space.

Due to the conservation of charge however, those input functions have the following restriction:

\frac{\partial ρ}{\partial t} + \nabla \cdot J = 0

Equation 1.

Charge conservation

Also consider the following cases:

if a spherical charge is moving, then this of course means that $ρ$ is changing with time, and at the same time that a current exists
in an ideal infinite cylindrical wire however, we can have constant $ρ$ in the wire, but there can still be a current because those charges are moving
Such infinite cylindrical wire is of course an ideal case, but one which is a good approximation to the huge number of electrons that travel in a actual wire.

The goal of finding

E

and

B

is that those fields allow us to determine the force that gets applied to a charge via the Equation "Lorentz force", and then to find the force we just need to integrate over the entire body.

Finally, now that we have defined all terms involved in the Maxwell equations, let's see the equations:

d i v E = \frac{ρ}{ε _{0}}

Equation 2.

Gauss' law

d i v B = 0

(3)

Equation 3.

Gauss's law for magnetism

\nabla \times E = - \frac{\partial B}{\partial t}

(4)

Equation 4.

Faraday's law

\nabla \times B = μ_{0} (J + ε_{0} \frac{\partial E}{\partial t})

(5)

Equation 5.

Ampere's circuital law

You should also review the intuitive interpretation of divergence and curl.

Lorentz force

force_density = ρ E + J \times B

Equation 1.

Lorentz force

A little suspicious that it bears the name of Lorentz, who is famous for special relativity, isn't it? See: Maxwell's equations require special relativity.

Ampère's force law

Force between two wires carrying an electric current.

Caused by the Lorentz force.

Explicit scalar form of the Maxwell's equations

For numerical algorithms and to get a more low level understanding of the equations, we can expand all terms to the simpler and more explicit form:

\frac{\partial E _{x}}{\partial x} + \frac{\partial E _{y}}{\partial x} + \frac{\partial E _{z}}{\partial x} = \frac{ρ}{ε _{0}} \frac{\partial B _{x}}{\partial x} + \frac{\partial B _{y}}{\partial x} + \frac{\partial B _{z}}{\partial x} = 0 \frac{\partial E _{z}}{\partial y} - \frac{\partial E _{y}}{\partial z} = - \frac{\partial B _{x}}{\partial t} \frac{\partial E _{x}}{\partial z} - \frac{\partial E _{z}}{\partial x} = - \frac{\partial B _{y}}{\partial t} \frac{\partial E _{y}}{\partial x} - \frac{\partial E _{x}}{\partial y} = - \frac{\partial B _{z}}{\partial t} \frac{\partial B _{z}}{\partial y} - \frac{\partial B _{y}}{\partial z} = μ_{0} (J_{x} + ε_{0} \frac{\partial E _{x}}{\partial t}) \frac{\partial B _{x}}{\partial z} - \frac{\partial B _{z}}{\partial x} = μ_{0} (J_{y} + ε_{0} \frac{\partial E _{y}}{\partial t}) \frac{\partial B _{y}}{\partial x} - \frac{\partial B _{x}}{\partial y} = μ_{0} (J_{z} + ε_{0} \frac{\partial E _{z}}{\partial t})

Equation 1

Overdetermination of Maxwell's equations

As seen from explicit scalar form of the Maxwell's equations, this expands to 8 equations, so the question arises if the system is over-determined because it only has 6 functions to be determined.

As explained on the Wikipedia page however, this is not the case, because if the first two equations hold for the initial condition, then the othe six equations imply that they also hold for all time, so they can be essentially omitted.

It is also worth noting that the first two equations don't involve time derivatives. Therefore, they can be seen as spacial constraints.

TODO: the electric field and magnetic field can be expressed in terms of the electric potential and magnetic vector potential. So then we only need 4 variables?

Bibliography:

physics.stackexchange.com/questions/20071/do-maxwells-equations-overdetermine-the-electric-and-magnetic-fields

Coulomb's law

Static case of Maxwell's law for electricity only.

Is implied by Gauss' law if Maxwell's equations: physics.stackexchange.com/questions/44418/are-the-maxwells-equations-enough-to-derive-the-law-of-coulomb

The "static" part is important: if this law were true for moving charges, we would be able to transmit information instantly at infinite distances. This is basically where the idea of field comes in.

Coulomb's Law experiment with torsion balance with a mirror on the balance to amplify rotations by uclaphysics (2010)

Source.

Solutions of Maxwell's equations

Understanding Electromagnetic Radiation! by Learn Engineering (2019)

Source. Shows animations of a dipole antenna which illustrates well how radiation is emitted from moving charges and travels at the speed of light.

Maxwell's equations with pointlike particles

In the standard formulation of Maxwell's equations, the electric current is a convient but magic input.

Would it be possible to use Maxwell's equations to solve a system of pointlike particles such as electrons instead?

The following suggest no, or only for certain subcases less general than Maxwell's equations:

This is the type of thing where the probability aspect of quantum mechanics seems it could "help".

Maxwell's equations in 2D

TODO it would be awesome if we could de-generalize the equations in 2D and do a JavaScript demo of it!

Not sure it is possible though because the curl appears in the equations:

Existence and uniqueness of solutions to Maxwell's equations

TODO: I'm surprised that the Wiki page barely talks about it, and there are few Google hits too! A sample one: www.researchgate.net/publication/228928756_On_the_existence_and_uniqueness_of_Maxwell's_equations_in_bounded_domains_with_application_to_magnetotellurics

Electric field ( $E$ )

Electric charge

Electric charge measure unit

Coulomb (C)

Charge conservation

Electric current

In the context of Maxwell's equations, it is vector field that is one of the inputs of the equation.

Section "Maxwell's equations with pointlike particles" asks if the theory would work for pointlike particles in order to predict the evolution of this field as part of the equations themselves rather than as an external element.

Measured in amperes in the International System of Units.

Electric potential ( $ϕ$ )

Volt (V)

Voltmeter

Nanovoltmeter

Voltage

Electronvolt

After the 2019 redefinition of the SI base units it is by definition exactly

1.6021766341 0^{- 19}

Joules.

Hall effect

The voltage changes perpendicular to the current when magnetic field is applied.

Figure 1.
Hall effect experimental diagram
. Source. The Hall effect refers to the produced voltage $V_{H}$ , AKA $V_{y}$ on this setup.

An intuitive video is:

Video 1. Source.

The key formula for it is:

V_{H} = \frac{I _{x} B _{z}}{n t e}

where:

$I_{x}$ : current on x direction, which we can control by changing the voltage $V_{x}$
$B_{z}$ : strength of transversal magnetic field applied
$n$ : charge carrier density, a property of the material used
$t$ : height of the plate
$e$ : electron charge

Applications:

the direction of the effect proves that electric currents in common electrical conductors are made up of negative charged particles
measure magnetic fields, TODO vs other methods

Other more precise non-classical versions:

quantum Hall effect

Bibliography:

hyperphysics.phy-astr.gsu.edu/hbase/magnetic/Hall.html

Hall resistance ( $R_{x y}$ , $R_{H}$ )

In some contexts, we want to observe what happens for a given fixed magnetic field strength on a specific plate (thus

t

and

n

are also fixed).

In those cases, it can be useful to talk about the "Hall resistance" defined as:

R_{x y} = \frac{V _{y}}{I _{x}}

So note that it is not a "regular resistance", it just has the same dimensions, and is more usefully understood as a proportionality constant for the voltage given an input

I_{x}

current:

V_{y} = R_{x y} I_{x}

This notion can be useful because everything else being equal, if we increase the current

I_{x}

, then

V_{y}

also increases proportionally, making this a way to talk about the voltage in a current independent manner.

And this is particularly the case for the quantum Hall effect, where

R_{x y}

is constant for wide ranges of applied magnetic field and TODO presumably the height

t

can be made to a single molecular layer with chemical vapor deposition of the like, and if therefore fixed.

Charge carrier density ( $n$ )

Hall effect sensor

Electromagnetic four-potential

A different and more elegant way to express Maxwell's equations by using the:

instead of the:

Electromagnetic tensor ( $F^{μ ν}$ )

Four-current

Lorentz gauge condition

There are several choices of electromagnetic four-potential that lead to the same physics.

E.g. thinking about the electric potential alone, you could set the zero anywhere, and everything would remain be the same.

The Lorentz gauge is just one such choice. It is however a very popular one, because it is also manifestly Lorentz invariant.

Coulomb gauge

Alternative to the Lorentz gauge, but less used in general as it is not as nice for relativity invariance.

Magnetism

Magnetic field ( $B$ )

Magnetic B and H field

electronics.stackexchange.com/questions/94744/what-is-the-difference-between-the-magnetic-h-field-and-the-b-field

Tesla (unit, T)

Magnetic moment

Magnetometer

Implementations:

Hall effect based, i.e. a Hall effect sensor
SQUID device

Magnetic flux

Magnetic vector potential ( $A$ )

Relativity

Special relativity

 3  0 

Explains how it is possible that everyone observes the same speed of light, even if they are moving towards or opposite to the light!!!

This was first best observed by the Michelson-Morley experiment, which uses the movement of the Earth at different times of the year to try and detect differences in the speed of light.

This leads leads to the following conclusions:

to length contraction and time dilation
the speed of light is the maximum speed anything can reach

All of this goes of course completely against our daily Physics intuition.

The "special" in the name refers to the fact that it is a superset of general relativity, which also explains gravity in a single framework.

Since time and space get all messed up together, you have to be very careful to understand what it means to say "I observed this to happen over there at that time", otherwise you will go crazy. A good way to think about is this:

use Einstein synchronization to setup a bunch of clocks for every position in your frame of reference
on every point of space, you put a little detector which records events and the time of the event
each detector can only detect events locally, i.e. events that happen very close to the detector
then, after the event, the detectors can send a signal to you, who is sitting at the origin, telling you what they detected

Invariance of the speed of light

This single experimental observation/idea is the basis for all of special relativity.

Special relativity is the direct result of people bending their backs to accommodate for this really weird fact.

History of special relativity

Bibliography:

Subtle is the Lord by Abraham Pais (1982) chapter III "Relativity, the special theory" has a good sketch as you may imagine.

Luminiferous aether

Can you just imagine what if luminiferous aether was one single fixed rigid body? This is apparently what Maxwell believed, Subtle is the Lord by Abraham Pais (1982) page 111 quoting his entry to Encyclopedia Britannica:

There can be no doubt that the interplanetary and interstellar spaces are not empty but are occupied by a material substance or body, which is certainly the largest, and probably the most uniform, body of which we have any knowledge.

Then it would provide a natural space coordinate for the entire universe!

Apparently Einstein was the first to completely say: let's just screw this aether thing completely then, it's getting too complicated, and we don't really need it. As Wikipedia puts it well, in very unencyclopedic tone^[ref]: Aether fell to Occam's razor.

Aether theory

Aether drag hypothesis

Given experiments such as the Fizeau experiment and the Michelson-Morley experiment that couldn't really detect the Earth's movement across aether, people started to wonder if the Earth wasn't dragging the luminiferous aether.

Lorentz ether theory

Special relativity experiment

moving magnet and conductor problem: the more experiments confirm Maxwell's equations, the more special relativity has to be correct
aberration TODO more precisely how it is evidence.

Aberration (astronomy)

Fizeau experiment

Michelson-Morley experiment (1987)

Published as On the Relative Motion of the Earth and the Luminiferous Ether.

Michelson Interferometer by Amrita Vlab (2013)

Source. Shows the optical controls and alignment in more detail.

Video 2.

Michelson Interferometer by TSG Physics (2012)

Source. TSG PHysiQuantum electrodynamics bibliographycs is the channel from the MIT Department of Physics Technical Services Group. In the video they produce a very clear round interference pattern.

On the Relative Motion of the Earth and the Luminiferous Ether (1987)

This paper is in the public domain and people have uploaded it e.g. to glorious Wikisource: en.wikisource.org/wiki/On_the_Relative_Motion_of_the_Earth_and_the_Luminiferous_Ether including its amazing illustrations.

Hafele-Keating experiment (Special relativity atomic clock on planes experiment)

Einstein synchronization

Frame of reference

Inertial frame of reference

Lorentz transformation

 3  0 

The equation that allows us to calculate stuff in special relativity!

Take two observers with identical rules and stopwatch, and aligned axes, but one is on a car moving at towards the

+ x

direction at speed

v

TODO image.

When both observe an event, if we denote:

$(t, x, y, z)$ the observation of the standing observer
$(t^{'}, x^{'}, y^{'}, z^{'})$ the observation of the ending observer on a car

It is of course arbitrary who is standing and who is moving, we will just use the term "standing" for the one without primes.

Then the coordinates of the event observed by the observer on the car are:

t^{'} x^{'} y^{'} z^{'} = γ (t - \frac{v x}{c ^{2}}) = γ (x - v t) = y = z

where:

γ = \frac{1}{1 - ( \frac{v}{c} ) ^{2}}

Note that if

\frac{v}{c}

tends towards zero, then this reduces to the usual Galilean transformations which our intuition expects:

t^{'} y^{'} z^{'} = t x^{'} = y = z = x - v t

(3)

This explains why we don't observe special relativity in our daily lives: macroscopic objects move too slowly compared to light, and

\frac{v}{c}

is almost zero.

Lorentz covariance

Same motivation as Galilean invariance, but relativistic version of that: we want the laws of physics to have the same form on all inertial frames, so we really want to write them in a way that is Lorentz covariant.

This is just the relativistic version of that which takes the Lorentz transformation into account instead of just the old Galilean transformation.

Lorentz invariant

Basically a synonym of Lorentz covariance?

Lorentz transform consequence: everyone sees the same speed of light

OK, so let's verify the main desired consequence of the Lorentz transformation: that everyone observes the same speed of light.

Observers will measure the speed of light by calculating how long it takes the light going towards

+ x

cross a rod of length

L = x_{2} - x_{1}

laid in the x axis at position

X 1

TODO image.

Each observer will observe two events:

$(t_{1}, x_{1}, y_{1}, z_{1})$ : the light touches the left side of the rod
$(t_{2}, x_{2}, y_{2}, z_{2})$ : the light touches the right side of the rod

Supposing that the standing observer measures the speed of light as

c

and that light hits the left side of the rod at time

T 1

, then he observes the coordinates:

t_{1} x_{1} t_{2} x_{2} = T 1 = X 1 = \frac{L}{c} = X 1 + L

Now, if we transform for the moving observer:

t_{1}^{'} x_{1}^{'} t_{2}^{'} x_{2}^{'} = γ (t_{1} - \frac{v x _{1}}{c ^{2}}) = γ (x_{1} - v t_{1}) = γ (t_{2} - \frac{v x _{2}}{c ^{2}}) = γ (x_{2} - v t_{2})

and so the moving observer measures the speed of light as:

c^{'} = \frac{x _{2}^{'} - x _{1}^{'}}{t _{2}^{'} - t _{1}^{'}} = \frac{( x _{2} - v t _{2} ) - ( x _{1} - v t _{1} )}{( t _{2} - \frac{v x _{2}}{c ^{2}} ) - ( t _{1} - \frac{v x _{1}}{c ^{2}} )} = \frac{( x _{2} - x _{1} ) - v ( t _{2} - t _{1} )}{( t _{2} - t _{1} ) - \frac{v}{c ^{2}} ( x _{2} - x _{1} )} = \frac{\frac{x _{2} - x _{1}}{t _{2} - t _{1}} - v}{1 - \frac{v}{c ^{2}} \frac{x _{2} - x _{1}}{t _{2} - t _{1}}} = \frac{c - v}{1 - \frac{v}{c ^{2}} c} = \frac{c - v}{\frac{c - v}{c}} = c

(3)

Length contraction

Suppose that a rod has is length

L

measured on a rest frame

S

(or maybe even better: two identical rulers were manufactured, and one is taken on a spaceship, a bit like the twin paradox).

Question: what is the length

L^{'}

than an observer in frame

S^{'}

moving relative to

S

as speed

v

observe the rod to be?

The key idea is that there are two events to consider in each frame, which we call 1 and 2:

the left end of the rod is an observation event at a given position at a given time: $x_{1}$ and $t_{1}$ for $S$ or $x_{1}^{'}$ and $t_{1}^{'}$ for $S^{'}$
the right end of the rod is an observation event at a given position at a given time : $x_{2}$ and $t_{2}$ for $S$ or $x_{2}^{'}$ and $t_{2}^{'}$ for $S^{'}$

Note that what you visually observe on a photograph is a different measurement to the more precise/easy to calculate two event measurement. On a photograph, it seems you might not even see the contraction in some cases as mentioned at en.wikipedia.org/wiki/Terrell_rotation

Measuring a length means to measure the

x_{2} - x_{1}

difference for a single point in time in your frame (

t 2 = t 1

So what we want to obtain is

x_{2}^{'} - x_{1}^{'}

for any given time

t^{'} 2 = t^{'} 1

In summary, we have:

L L^{'} = x_{2} = x_{2}^{'} - x_{1} - x_{1}^{'} t_{2}^{'} = t_{1}^{'}

By plugging those values into the Lorentz transformation, we can eliminate

t_{2} a n d t_{1}

, and conclude that for any

t_{2}^{'} = t_{1}^{'}

, the length contraction relation holds:

L^{'} = \frac{L}{γ}

The key question that needs intuitive clarification then is: but how can this be symmetric? How can both observers see each other's rulers shrink?

And the key answer is: because to the second observer, the measurements made by the first observer are not simultaneous. Notably, the two measurement events are obviously spacelike-separated events by looking at the light cone, and therefore can be measured even in different orders by different observers.

Terrell rotation

What you would see the moving rod look like on a photo of a length contraction experiment, as opposed as using two locally measured separate spacetime events to measure its length.

Time dilation

 3  0 

One of the best ways to think about it is the transversal time dilation thought experiment.

Transversal time dilation

Light watch transverse to direction of motion. This case is interesting because it separates length contraction from time dilation completely.

Of course, as usual in special relativity, calling something "time dilation" leads us to mind boggling ideas of "symmetry breaking": if both frames have a light watch, how can both possibly observe the other to be time dilated?

And the answer to this, is the usual: in special relativity time and space are interwoven in a fucked up way, everything is just a spacetime event.

In this case, there are three spacetime events of interest: both clocks start at same position, your beam hits up at x=0, moving frame hits up at x>0.

Those two mentioned events are spacelike-separated events, and therefore even though they seem simultaneous to you, they are not going to be simultaneous to the moving observer!

If little clock one meter away from you tells you that at the time of some event (your light beam hit up) the moving light watch was only 50% up, this is just a number given by your one meter away watch!

Transverse Doppler effect

Twin paradox

The key question is: why is this not symmetrical?

One answer is: because one of the twin accelerates, and therefore changes inertial frames.

But the better answer is: understand what happens when the stationary twin sends light signals at constant time intervals to each other. When does the travelling twin receives them?

By doing that, we see that "all the extra aging happens immediately when the twin turns around":

on the out trip, both twins receive signals at constant intervals
when the moving twin turns around and starts to accelerate through different inertial frames, shit happens:
- the moving twin suddenly notices that the rate of signals from the stationary twin increased. They are getting older faster than us!
- the stationary twin suddenly notices that the rate of signals from the moving twin decreased. They are getting older slower than us!
then when the moving twin reaches the return velocity, both see constant signal rates once again

Figure 1.
Twin paradox illustration with twins sending light signals at regular intervals
. Source.

Another way of understanding it is: you have to make all calculations on a single inertial frame for the entire trip.

Supposing the sibling quickly accelerates out (or magically starts moving at constant speed), travels at constant speed, and quickly accelerates back, and travels at constant speed setup, there are three frames that seem reasonable:

the frame of the non-accelerating sibling
the outgoing trip of the accelerating sibling
the return trip of the accelerating sibling

If you do that, all three calculations give the exact same result, which is reassuring.

Another way to understand it is to do explicit integrations of the acceleration: physics.stackexchange.com/questions/242043/what-is-the-proper-way-to-explain-the-twin-paradox/242044#242044 This is the least insightful however :-)

Bibliography:

Maxwell's equations require special relativity

The following aspects of Maxwell's equations make no sense without special relativity:

the Lorentz force would be different observers have different speeds, see e.g.: charged particle moving at the same speed of electrons thought experiment
Maxwell's equations imply that the speed of light is the same for all inertial reference frames

When charged particle though experiment are seen from the point of view of special relativity, it becomes clear that magnetism is just a direct side effect of charges being viewed in special relativity. One is philosophically reminded of how spin is the consequence of quantum mechanics + special relativity.

Bibliography:

Deriving magnetism from electricity and relativity

It appears that Maxwell's equations can be derived directly from Coulomb's law + special relativity:

This idea is suggested by the charged particle moving at the same speed of electrons thought experiment, which indicates that magnetism is just a consenquence of special relativity.

Why moving charges produce magnetic field? by FloatHeadPhysics (2022)

Source.

Moving magnet and conductor problem (Charged particle moving at the same speed of electrons thought experiment)

This is a well known though experiment, which Richard Feynman used to emphasize

infinite wire with balanced positive and negative charges, so no net charge, but a net magnetic field
a single charge moves parallel to wire at the same speed as the electrons

In the above experiment:

from the wire frame, the charge feels electromagnetic force, because it is moving and there is a magnetic field
from the single charge frame, there is still magnetic field (positive charges are moving), but the body itself is not moving, so there is no force!

The solution to this problem is length contraction: the positive charges are length contracted and the moving electrons aren't, and therefore they are denser and therefore there is an effective charge from that frame.

This is also mentioned at David Tong www.damtp.cam.ac.uk/user/tong/em/el4.pdf (archive) "David Tong: Lectures on Electromagnetism - 5. Electromagnetism and Relativity" "5.2.1 Magnetism and Relativity".

How Special Relativity Fixed Electromagnetism by The Science Asylum (2019)

Source.

Covariant formulation of classical electromagnetism

Maxwell's equations are Lorentz invariant

Subtle is the Lord by Abraham Pais (1982) chapter III "Relativity, the special theory" mentions that this fact and its importance (we want the laws of physics to look the same on all inertial frames, AKA Lorentz covariance) was first fully relized by poincaré in 1905.

And at that same time poincaré also immediately started to think about the other fundamental force then known: gravity, and off the bat realized that gravitational waves must exist. general relativities is probably just "the simplest way to make gravity Lorentz covariant".

Bibliography:

physics.stackexchange.com/questions/219474/proof-that-maxwell-equations-are-lorentz-invariant

Maxwell's equations imply that the speed of light is the same for all inertial reference frames

Maxwell Lagrangian

www.youtube.com/watch?v=nrBiDRZRK5g Maxwell Lagrangian Derivation by Dietterich Labs (2019)
www.youtube.com/watch?v=yo-Z3RO-eeY Deriving the Maxwell Lagrangian by Pretty Much Physics (2019)

R^{4}

with a weird dot product-like operation called the Minkowski inner product.

Because the Minkowski inner product product is not positive definite, the norm induced by an inner product is a norm, and the space is not a metric space strictly speaking.

The name given to this type of space is a pseudometric space.

Minkowski inner product

This form is not really an inner product in the common modern definition, because it is not positive definite, only a symmetric bilinear form.

Minkowski inner product matrix ( $η_{μ ν}$ )

The matrix representation of the symmetric bilinear form that is the Minkowski inner product.

Since that is a symmetric bilinear form, the associated matrix is a symmetric matrix.

By default, we will use the time negative representation unless stated otherwise:

η_{μ ν} = ⎣ ⎢ ⎢ ⎢ ⎡ - 1 000 010000100001 ⎦ ⎥ ⎥ ⎥ ⎤

but another equivalent one is to use a time positive representation:

η_{μ ν} = ⎣ ⎢ ⎢ ⎢ ⎡ 1000 0 - 1 00 00 - 1 0 000 - 1 ⎦ ⎥ ⎥ ⎥ ⎤

The matrix is typically denoted by the Greek letter eta.

Spacetime diagram

Why should I care when I can calculate new x and new time with Lorentz transformation?

Answer: it can give some qualitative intuition on what is larger/smaller happens before/after based only on arguably more intuitive geometric considerations, without requiring you to do any calculations, see e.g. Figure "Spacetime diagram illustrating how faster-than-light travel implies time travel".

Light cone

A subset of Spacetime diagram.

The key insights that it gives are:

future and past are well defined: every reference frame sees your future in your future cone, and your past in your past cone
Otherwise causality could be violated, and then things would go really bad, you could tell your past self to tell your past self to tell your past self to do something.
You can only affect the outcome of events in your future cone, and you can only be affected by events in your past cone. You can't travel fast enough to affect.
Two spacetime events with such fixed causality are called timelike-separated events.
every other event (to right and left, known as spacelike-separated events) can be measured to happen before or after your current spacetime event by different observers.
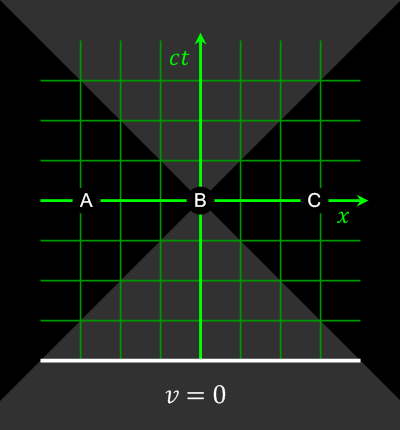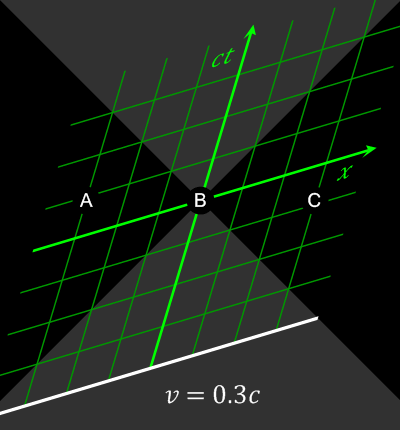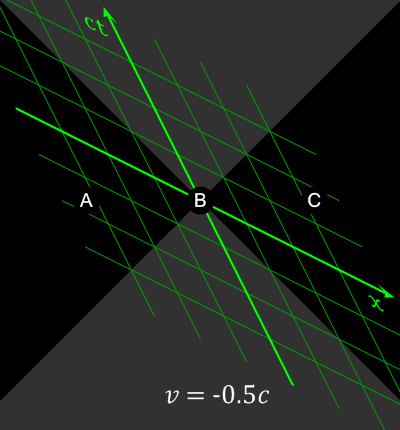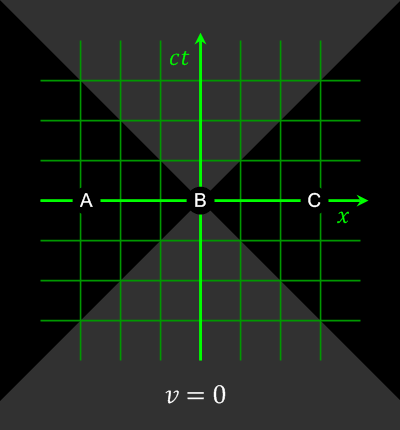
But that does not violate causality, because you just can't reach those spacetime points anyways to affect them.

Figure 1.
Animation showing how space-separated events can be observed to happen in different orders by observers in different frames of reference
. Source.

Timelike-separated event

The opposite of spacelike-separated events.

Spacelike-separated event

Mathematically, we can decide if two events are timelike-separated or spacelike-separated by just looking at the sign of the spacetime interval between them.

On the light cone, these are events on the left/right part of the cone.

Different observers might not agree on the order of two spacelike-separated events.

Further discussion at Section "Light cone".

The opposite of those events are timelike-separated events.

time
length, given by the Pythagorean theorem

However, in special relativity, neither of those are invariant separately, since space and time are mixed up together.

Instead, there is a new unified invariant: the spacetime-interval, given by:

c Δ t^{2} - (Δ x^{2} + Δ y^{2} + Δ z^{2})

Note that this distance can be zero for two events separated.

Proper time

General relativity