Luminiferous aether Updated 2025-07-16
Can you just imagine what if luminiferous aether was one single fixed rigid body? This is apparently what Maxwell believed, Subtle is the Lord by Abraham Pais (1982) page 111 quoting his entry to Encyclopedia Britannica:Then it would provide a natural space coordinate for the entire universe!
There can be no doubt that the interplanetary and interstellar spaces are not empty but are occupied by a material substance or body, which is certainly the largest, and probably the most uniform, body of which we have any knowledge.
Machine learning Updated 2025-07-16
The main reason Ciro Santilli never touched it is that it feels that every public data set has already been fully mined or has already had the most interesting algorithms developed for it, so you can't do much outside of big companies.
This is why Ciro started Ciro's 2D reinforcement learning games to generate synthetic data and thus reduce the cost of data.
The other reason is that it is ugly.
Machine learning as a form of data compression Updated 2025-07-16
Machine learning company Updated 2025-07-16
This section is about companies that primarily specialize in machine learning.
The term "machine learning company" is perhaps not great as it could be argued that any of the Big tech are leaders and sometimes, especially in the case of Google, has a main product that is arguably a form of machine learning.
MacOS Updated 2025-07-16
Nice looking and expensive operating system by Apple. Ciro Santilli believes that:
- if you want to be ripped off, just use Microsoft Windows which has more software available
- or if you want to attain Enlightenment, just use Linux, which is free and open source
Madelung energy ordering rule Updated 2025-07-16
Looking at the energy level of the Schrödinger equation solution for the hydrogen atom, you would guess that for multi-electron atoms that only the principal quantum number would matter, azimuthal quantum number getting filled randomly.
However, orbitals energies for large atoms don't increase in energy like those of hydrogen due to electron-electron interactions.
In particular, the following would not be naively expected:
This rule is only an approximation, there exist exceptions to the Madelung energy ordering rule.
Magic Aids Updated 2025-07-16
His combination of politically incorrect dirt talk with amazing quirky decks captures Ciro's imagination.
Anonymous no face-reveal.
The videos are heavily edited with all pauses cut out, which makes them very quick to watch and saves viewer time.
Modern focused, with some occasional newer formats mixed in.
When Wizards publishes several useless sets in a row without a single modern playable card, he's just forced into Standard.
Ciro Santilli's body Updated 2025-07-16
31 year old:
- Height:
- Weight:
- Chest: 94cm
- Waist: 81.5cm
- Hip: 85.5cm
- Inner leg: 92.0cm
- Length of back: 71cm (from base of neck to knuckle height)
- Collar: 38cm
- Sitbone distance (ischial tuberosity):
- sitting on cardboard: 110mm, this method felt accurate
- www.youtube.com/watch?v=xSWlwzqGKik water method: 90mm/100mm. Small butt!?
- Arm sleeve length: 61.5 cm
- Head circumference: 58.5 cm
- Hand:
- circumference: 19.8 cm around open hand knuckle
- Tip Of Middle Finger To Crease Under Palm: 20 cm
- Circunference around closed knuckle: 25 cm
- Hand great span en.wikipedia.org/wiki/Span_(unit): 0.22m
- Erect penis length: just kidding, just kidding. Ciro Santilli's wife would kill him.
- rest heart rate: 60 BPM
Magic: The Gathering meta-based deck choice is a bimatrix game Updated 2025-07-16
Ciro had initially Googled for the "4-card limit thought experiment" but he reached: www.channelfireball.com/articles/what-if-the-4-card-limit-was-abolished-in-modern/ "What if the 4-Card Limit Was Abolished in Modern?" by Frank Karsten (2018) and was much more pleased with the mathematical result. Like-minded people.
That links to www.channelfireball.com/articles/what-if-the-4-card-limit-was-abolished-in-modern/ the related article: "The Mythic Invitational's Duo Standard Format Game Theory Optimized" by Frank Karsten (2019) which explains well how Nash equilibrium is naturally reached: if there is any imbalance, someone can take advantage of it, and then it rebalances. Therefore once you've calculated the equilibrium, your best course of action is to pick a deck at random from a list of possible winners.
Hertz electromagnetic wave experiments Updated 2025-07-16
Heinrich Hertz's main initial experiment used a spark-gap transmitter. It is not something that transmits recorded sounds like voice: it only transmits noisy beeps. And as such was used for wireless telegraphy.
- a piezo igniter from a barbequeue lighter
- a more powerful home-made transformer
Hertz and Radio waves Explained by PhysicsHigh (2016)
Source. Simple schematics showing the basics of the experiments. No choice of components rationale. Magic the gathering's banning of 7 cards due to "racism" (2020) Updated 2025-07-16
Official announcement: magic.wizards.com/en/articles/archive/news/depictions-racism-magic-2020-06-10
List of cards with images: www.hipstersofthecoast.com/2020/06/wizards-bans-7-cards-that-depict-racism-including-invoke-prejudice/
- Invoke prejudice: depicts the Ku Klux Klan. Card's title clearly criticizes them "prejudice".
- Stone-Throwing Devils: not sure about this one: boardgames.stackexchange.com/questions/54341/what-is-offensive-about-the-card-stone-throwing-devils
- Cleanse: it does not seem to have any reference to black people, image depicts fantastic animals. There are hundreds of cards that talk about black since it is one of the 5 colors of magic.
- Pradesh Gypsies: does not appear to suggest any bad things about gypsies, on the contrary
- Jihad: does not appear to suggest any bad things about Islam, on the contrary
- Imprison: depicts a black slave. Let's pretend it never happened.
- Crusade: pretend it never happened
Magnetic dipole Updated 2025-07-16
A tiny idealized magnet! It is a very good model if you have a small strong magnet interacting with objects that are far away, notably other magnetic dipoles or a constant magnetic field.
The cool thing about this model is that we have simple explicit formulas for the magnetic field it produces, and for how this little magnet is affected by a magnetic field or by another magnetic dipole.
Quotient group Updated 2025-07-16
Ultimate explanation: math.stackexchange.com/questions/776039/intuition-behind-normal-subgroups/3732426#3732426
Does not have to be isomorphic to a subgroup:
This is one of the reasons why the analogy between simple groups of finite groups and prime numbers is limited.
Magnetic resonance imaging Updated 2025-07-16
How MRI Works Part 1 by thePIRL (2018)
Source. - youtu.be/TQegSF4ZiIQ?t=326 the magnet is normally always on for the entire lifetime of the equipment!
- youtu.be/TQegSF4ZiIQ?t=465 usage of non-ionizing radiation (only radio frequencies) means that it is very safe to use. The only dangerous part is the magnetic field interacting with metallic objects.
Dr Mansfield's MRI MEDICAL MARVEL by BBC
. Source. Broadcast in 1978. Description:Tomorrow's World gave audiences a true world first as Dr Peter Mansfield of the University of Nottingham demonstrated the first full body prototype device for Magnetic resonance imaging (MRI), allowing us to see inside the human body without the use of X-rays.
Maiden Voyage by Herbie Hancock (1965) Updated 2025-07-16
randyscotsmithey/feathers-realworld-example-app Updated 2025-07-16
FeathersJS entry for gothinkster/realworld.
MongoDB-based.
So once you install MongoDB, run with:
MONGODB_FEATHERS_REALWORLD=mongodb://localhost:27017/mydb npm startGot it working on Ubuntu 20.10 with both React and Vue.js front-ends at github.com/randyscotsmithey/feathers-realworld-example-app/commit/8bc3a09242285de624c75bb8345630df499a7d07 as mentioned at github.com/randyscotsmithey/feathers-realworld-example-app/issues/2 except for bad error reporting on UI.
Tests can be run with:but there were 10 failures and 55 passes: github.com/randyscotsmithey/feathers-realworld-example-app/issues/3
MONGODB_FEATHERS_REALWORLD=mongodb://localhost:27017/mydb npm run test Raspberry Pi OS Updated 2025-07-16
Change password without access:
Enable SSH on boot:
sudo touch /boot/ssh
Ciro Santilli's campaign for freedom of speech in China Updated 2025-07-16
Centerpiece: github.com/cirosantilli/china-dictatorship
Fully rendered at: github.com/china-dictatorship
The campaign has centered around publishing censored keywords on his Stack Overflow username, thus using his considerable Stack Overflow presence to sabotage the website in China. Here is an early web archive.
Chrysanthemum Xi Jinping with 六四 spice added by Ciro Santilli
. This was one of the profile pictures that Ciro Santilli used as part of his campaign.
Ciro later went on to prefer the "unmodified" Xi Jinping photo cover of some edition Xi Jinping Though, which also reminds Ciro very much of religious devotional pictures, e.g. those of Li Hongzhi.
Ciro understood that the best propaganda against a dictatorial enemy is recontextualized unmodified propaganda produced by the enemy itself. Their propaganda speaks for itself
Like most people in the West, Ciro has always been for political freedom of speech, and therefore against the Chinese government's policies.
However, the seriousness of the matter only fully dawned on him in 2015 when, his mother-in-law, a then a 63-year-old lady, was put into jail for 15 days for doing Falun Gong.
And all of this was made 100 times worse because Ciro deeply loves several aspects of China, such as food, language, art and culture, and saw it all being destroyed by the Communists: cirosantilli.com/china-dictatorship/does-ciro-santilli-hate-china
The rationale of this is to force the Chinese government to either:
- leave things as they are, and let censored keywords appear on Stack Overflow (most likely scenario)
- block Stack Overflow, and lose billions of dollars with worse IT technology
- disable the Great Firewall
In the beginning, this generated some commotion, but activity reduced as novelty wore off, and as he collected the reply to all possible comments at: github.com/cirosantilli/china-dictatorship.
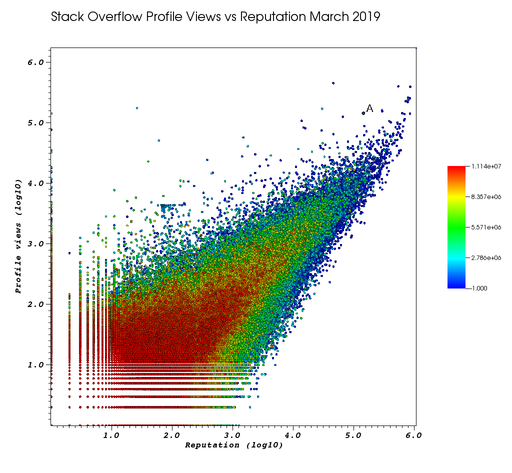
This campaign has led him to have an insane profile view/reputation ratio, since many people pause to look at his profile. He is point "A" at the top right corner of Figure 2. "Scatter plot of Stack Overflow user reputation vs profile views in March 2019 with Ciro Santilli marked as A":
Ciro feels that the view count started increasing more slowly since 2020 compared to his reputation, likely every single Chinese user has already viewed the profile.
Further analysis has been done at: stats.stackexchange.com/questions/376361/how-to-find-the-sample-points-that-have-statistically-meaningful-large-outlier-r
Ciro Santilli with a stone carved Budai in the Feilai Feng caves near the Lingyin Temple in Hangzhou taken during his legendary 2012 touristic trip to China
. Will he ever be able to go to China again to re-experience such marvelous locations?Water Margin tribute to Chinese dissidents by Ciro Santilli (2022)
Source. More information: cirosantilli.com/china-dictatorship/water-margin Hewlett-Packard Updated 2025-07-16
They do seem to have been very innovative, and have had a very good work culture. They also had a huge impact on the Silicon Valley startup scene.
Some products they are known for:
- oscilloscopes
- Atomic clocks, notably highly portable ones, see e.g. Video "Inside the HP 5061A Cesium Clock by CuriousMarc (2020)"
- pocket calculator
Making the Cisco connection Updated 2025-07-16
Nothing phenomenally new on the early days to add on top of Video "Nerds 2.0.1 excerpt about Cisco (1998)", but a few new good points:
- Cisco at one point became the largest company by market capitalization. This wore off a bit as of 2020.They used this overvalued stock in part to buy many other (often also overvalued) up and coming companies. This acquisition spree strategy was apparently not the norm at the time. rohitnair.wordpress.com/2011/12/13/cisco-history-cisco-systems-history-and-trivia-brand-history-and-trivia/ mentions they have bought more than 140 companies since, and that they call this strategy "Build, Buy And Partner"
- a big part of what Cisco did was to allow cheap local communication in-campus. At that time, the ARPANET was already up and running, but their "routers", called Interface Message Processors were very expensive at about $100,000, and to send data across the campus you had to go through them, which meant expensive bandwidth. The routers sometimes failed, and the fallback was to send students around with disks: "sneakernet". They needed new local protocols and hardware to efficiently connect different campus networks.
- Sandy Lerner nude photo
- Cisco was a pioneer in having an Internet support forum. Customers could also help one another. This was fundamental in scaling support, as they grew so fast it would be impossible to hire a support team large enough without the help of the forum.
- Cisco gave out source code to some customers who would then implement protocols they cared about, and Cisco would then merge it back
There are unlisted articles, also show them or only show them.