High temperature superconductor superconducting magnet Updated 2025-07-16
History Updated 2025-07-16
Messaging software that force you to have a mobile phone Updated 2025-07-16
Chat programs that don't have a proper web-only operation and force you to have a mobile phone, e.g. WhatsApp.
Heck, even Signal, which is supposed to be super secure and good for your privacy, forces you to disclose your freaking cell phone to all contacts! lifehacker.com/how-to-use-signal-without-revealing-your-private-phone-1818996580
Meta breaking glitch Updated 2025-07-16
A meta breaking glitch of a video game is a glitch that when discovered significantly breaks the meta.
In non-video game-game, it does sometimes happen that a meta is broken as well, but these events tend to be rarer and less dramatic than meta-breaking due to computer program glitches.
In PvP games, those glitches are generally forbidden by existing rules, and quickly patched after discovered.
In speedrunning however, they are either incorporated in the existing strategy, or may lead to the creation of a new run category for particularly significant glitches.
Ciro Santilli's psychology Updated 2025-07-16
Ciro Santilli's skills Updated 2025-07-16
Ciro Santilli's software engineering wisdom Updated 2025-07-16
Of course, "Ciro Santilli" with quotes, since all of those are either taken directly from others, or had been previously formulated by others.
Metagenomics Updated 2025-07-16
Experiments that involve sequencing bulk DNA found in a sample to determine what species are present, as opposed to sequencing just a single specific specimen. Examples of samples that are often used:
- river water to determine which bacteria are present, notably to determine if the water is free of dangerous bacteria. A concrete example is shown at: Section "How to use an Oxford Nanopore MinION to extract DNA from river water and determine which bacteria live in it".
- sea water biodiversity: ocean-microbiome.embl.de/companion.html
- food, including searching for desirable microorganisms such as in cheese or bread yeast
- poo, e.g. to study how the human microbiome influences health. There are companies actively working on this, e.g.: www.microbiotica.com/
One related application which most people would not consider metagenomics, is that of finding circulating tumor DNA in blood to detect tumors.
Metric (mathematics) Updated 2025-07-16
A metric is a function that give the distance, i.e. a real number, between any two elements of a space.
Because a norm can be induced by an inner product, and the inner product given by the matrix representation of a positive definite symmetric bilinear form, in simple cases metrics can also be represented by a matrix.
History of DNA methylation research Updated 2025-07-16
Incredible that there hasn't been a Nobel Prize for it as of 2022, e.g. as mentioned at: theconversation.com/no-nobel-but-epigenetics-finally-gets-the-recognition-it-deserves-18970
Some old dudes getting another prize in 2016: www.cuimc.columbia.edu/news/pioneers-epigenetics-awarded-horwitz-prize
Michelson-Morley experiment Updated 2025-07-16
Michelson Interferometer by Amrita Vlab (2013)
Source. Shows the optical controls and alignment in more detail.Michelson Interferometer by TSG Physics (2012)
Source. TSG PHysiQuantum electrodynamics bibliographycs is the channel from the MIT Department of Physics Technical Services Group. In the video they produce a very clear round interference pattern. Michigan State University Updated 2025-07-16
Not to be confused with the University of Michigan. Not confusing at all right!
Micro Bit getting started Updated 2025-07-16
When plugged into Ubuntu 22.04 via the USB Micro-B the Micro Bit mounts as:e.g.:for username
/media/$USER/MICROBIT//media/ciro/MICROBIT/ciro.Loading the program is done by simply copying a The file name does not matter, only the
.hex binary into the image e.g. with:cp ~/Downloads/microbit_program.hex /media/$USER/MICROBIT/.hex extension. Ciro Santilli's Stack Overflow contributions Updated 2025-07-16
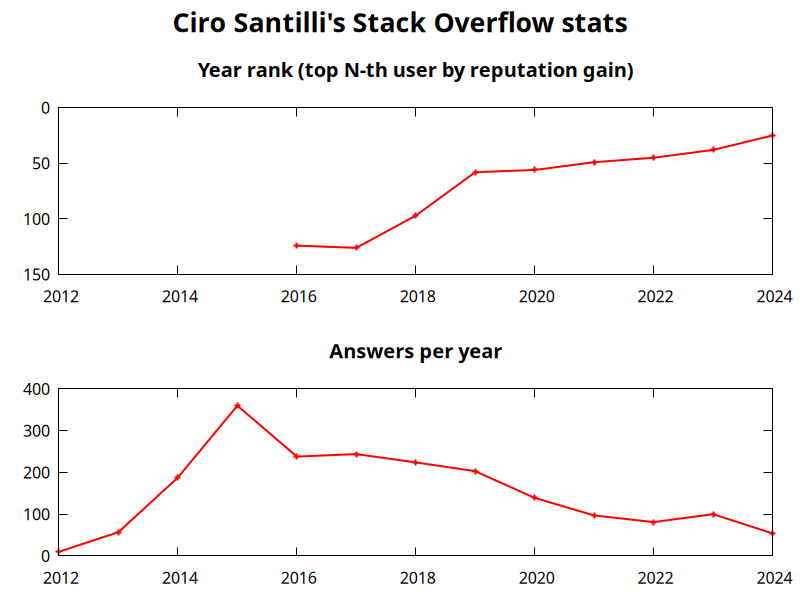
Ciro Santilli's Stack Overflow stats
. Data compiled for the plot: ciro-santilli-stack-overflow-stats.csv
- top obtained manually from pages such s=as: stackexchange.com/leagues/1/year/stackoverflow/2023-01-01
- answer count obtained with this Stack Exchange Data Explorer data.stackexchange.com/stackoverflow/query/433214/count-of-answers-by-user-over-time and then manually pasting it in.
- total questions obtained with: data.stackexchange.com/stackoverflow/query/1882511/questions-asked-per-year-on-stack-overflow#resultSets
Plot generated with gnuplot with ciro-santilli-stack-overflow-stats.gnuplot
Related announcements:
Ciro Santilli's Stack Overflow contributions have, unsurprisingly, centered around the subjects he has worked with: systems programming and web development, and necessary tooling to get those done, such as Git, Python, Bash and Ubuntu.
His best answers are listed at: Section "The best articles by Ciro Santilli".
Stack Overflow has been the initial centerpiece of Ciro Santilli's campaign for freedom of speech in China, until Ciro noticed that GitHub might be potentially even more effective for it.
In Stack Overflow Ciro likes to:
- answer important questions found through Google which he needs to solve an actual problem he has right now, and for which none of the existing answers satisfied him, and close duplicates.
- monitor less known tags which very few people know a lot about and where the knowledge sharing desperately lacking, but in which Ciro specializes and therefore has some uncommon knowledge to share
In practice it also happens that Ciro:
- Googles for his own answers to remember some detail he wrote down but with slightly different terms that were closer to mind at the time, and find other similar questions for which he has the perfect answer.
- learns something new by chance, e.g. some new flashy feature of a new version of the C++ standard, thinks "this is awesome, there must be a Stack Overflow question for it", and then there is a question and he answers it
When he gets an upvote on one of his more obscure answers, Ciro often re-reads it, and often finds improvements to be made and makes them.
He doesn't like to refresh the homepage looking for easy reputation on widely known subjects. See also: online forums that lock threads after some time are evil.
The result is that Ciro ends up getting relatively a lot of reputation without much work! The term passive income, much beloved by fake investment gurus, comes to mind. But now it's "passive reputation"! And it is useless! Yay!
For this reason, Necromancer is Ciro's favorite badge (get 5 upvotes on a question older than 60 days), and as of July 2019, he became the #1 user with the most of this badge. Announcement on Twitter.
The number two at the time was VonC (see also: Section "Epic Stack Overflow users"), who had about 16 times more answers than Ciro in total! From this query: data.stackexchange.com/stackoverflow/query/1072396?&Date=2019-07-01&UserId=895245 it can be seen that as of July 2019, 1216 out of his 1329 answers were answered 60 days after the questions and constitute potential necromancers! Compare that to VonC's 1643 potential necromancers out of 21767 answers!
VonC eventually took back the lead in 2022, dude's a machine!!! twitter.com/cirosantilli/status/1546389532014247936
Someone at Ciro's work once said something along:and this does ring true in Stack Overflow as well. When you are answering stuff, it means that you either didn't know, or that the information wasn't well available, and so your specific application is progressing slowly because of that. Once the generic prerequisites are well solved and answered, you will spend much more time on your business specific things rather than anything else that can be factored out across projects, and so you will get more "directly useful work" done, and less Stack Overflow answers. Of course, without the prior research in place, you can't get the final product done either.
In terms of per year reputation ranks, Ciro was in the top 100 in of the 2018 ranking with 38,710 reputation gained in that year: stackexchange.com/leagues/1/year/stackoverflow/2018-01-01?sort=reputationchange&page=4 (archive). He reached top 50 in 2022. Note that daily reputation is mostly capped to 200 per day, leading to a maximum 73000 per year. It is possible to overcome this limit either with bounties or accepts, and Ciro finds it amazing that some people actually break the 73k limit by far with accepts, e.g. Gordon Linoff reached 135k in 2018 (archive)! However, this is something that Ciro will never do, because it implies answering thousands and thousands of useless semi duplicate questions as fast as possible to get the accept. Ciro's reputation comes purely from upvotes on important question, and is therefore sustainable without any extra effort once achieved. Interestingly, Ciro appeared on top of the quarter SE rankings around 2019-11: web.archive.org/web/20191112100606/https://stackexchange.com/leagues but it was just a bug ;-)
There is no joy like answering an old question, and watching your better answer go up little by little until it dominates all others.
Stack Overflow reputation is of course, in itself, meaningless. People who contribute to popular subjects like web development will always have infinitely more reputation than those that contribute to low level subjects.
What happens on the specialized topics though is that you end up getting to know all the 5 users who contribute 95% of the content pretty soon as you study those subjects.
Like everything that man does, the majority of Ciro's answers are more or less superficial subjects that many people know but few have the patience to explain well, or they are updates to important questions reflecting upstream developments. But as long as they save 15 minutes from someone's life, that's fine.
There is great beauty when you are involved in a programming problem, and you suddenly remember: wait, I answered something related a few years ago! And especially so when you can go back and improve your old answer with new insight. This has great value, because when you were more newbie, you would have typed different words into Google Search than you would now. So by updating posts from when you were a newbie, you are helping other newbies more, as they are more likely to be also searching for those keywords. It is also very nice to have some head start on the answer's upvote count and not have to bootstrap yet another answer from 0 upvotes and have to go through all the competition!
For example, Ciro's most upvoted answer as of July 2019 is stackoverflow.com/questions/18875674/whats-the-difference-between-dependencies-devdependencies-and-peerdependencies/22004559#22004559 was written when he spent his first week playing with NodeJS (he was having a look at Overleaf, later merged into Overleaf, for education), which he didn't touch again for several years, and still hasn't "mastered" as of 2019! This did teach a concrete life lesson to Ciro however: it is impossible to know what is the most useful thing you can do right now very precisely. The best bet is to follow your instincts and do as much awesome stuff as you can, and then, with some luck, some of those attempts will cover an use case.
Ciro tends to take most pride on his systems programming answers, which is a subject that truly relatively few people know about. He likes it when he goes insanely deep into a subject, way beyond what OP had in mind, exposing full root causes and broader causes, see e.g.:
- stackoverflow.com/questions/1778538/how-many-gcc-optimization-levels-are-there/30308151#30308151
- stackoverflow.com/questions/34519521/why-does-gcc-create-a-shared-object-instead-of-an-executable-binary-according-to/55704865#55704865
- stackoverflow.com/questions/8352535/how-does-kernel-get-an-executable-binary-file-running-under-linux/31394861#31394861
Ciro also derives great joy from his "media related answers" (3D graphics, audio, video), which are immensely fun to write, and sometimes borderline art, see answers such as those under "OpenGL" and "Media" under the best articles by Ciro Articles or even simpler answers such as:
Figure 3. Ciro knows how to convert videos to GIFs.- Stereo "tone-generator" for linux?, related: FFmpeg sound synthesis
There is something of greater value in perfectly presented technical knowledge, that goes beyond than simply getting something done. The pleasure of understanding and mastering something, and perhaps of the explanation itself. Sometimes when answering, Ciro feels like a tailor, where ASCII is his cloth. See also: Section "The art of programming", Section "Physics and the illusion of life".
Ciro's deep understanding of Stack Overflow mechanisms and its shortcomings also helped shape his ideas for: OurBigBook.com. So it is a bit funny to think that after all time Ciro spent on the website, he actually wants to destroy it and replace it with something better. There can be no innovation without some damage. It also led to Ciro's creation of Stack Overflow Vote Fraud Script.
After answering so many questions, he ended up converging to a more or less consistent style, which he formalized at:Like any other style guide, this answer style guide, once fully incorporated and memorized, allows Ciro to write answers faster, without thinking about formatting issues.
- meta.stackexchange.com/questions/18614/style-guide-for-questions-and-answers/326746#326746. Key self-quote:
- meta.stackexchange.com/questions/10647/how-do-i-write-a-good-title/311903#311903. Question title style only. After a few years later more people agreeing with that post which now had -12 votes: meta.stackoverflow.com/questions/422082/should-we-add-option-use-complete-sentences-to-first-answers-queue
Ciro also made a question title style guide: meta.stackexchange.com/questions/10647/how-do-i-write-a-good-title/311903#311903 but for some reason the Stack Overflow community prefers their semi-defined title meta-language to proper English. Go figure.
Ciro started contributing to Stack Overflow in 2012 when he was at École Polytechnique.
Like all things that end up shaping the course of one's life, Ciro started contributing without thinking too much about it.
His first answer was to the LaTeX question: Standalone diagrams with TikZ?, which reflects the fact that this happened while Ciro was reaching his Ciro Santilli's Open Source Enlightenment.
Ciro's first upvote was for his 2012 question: How to run a Python script portably without specifying its full path?
When he started contributing, Ciro was still a newbie. One early event he will never forget was when someone mentioned a "man page", and Ciro commented saying that there was a typo!
When Ciro reached 15 points and gained the ability to upvote, it felt like a major milestone, he even took a screenshot of the browser! 1k, 10k and 100k were also particularly exciting. When the 100k cup (archive) arrived in 2018, Ciro made a show-off Facebook post (archive). At some point though, your brain stops caring, and automatically filters out any upvotes you get except on the answers that you are really proud of and which don't yet have lots of upvotes. The last remaining useless gamed achievement that Ciro looked forward to was legendary (archive), and which he achieved on 2021-02-16.
Ciro Santilli with his Stack Overflow 100k reputation cup
. From the start, Ciro's motivations for contributing to Stack Overflow have been a virtuous circle of:
- save the world through free education
- It feels especially amazing when people in the real world start taking note of you, and either close friends tell you straight out that you're a Stack Overflow God, or as you slowly and indirectly find out that less close know or came to you due to your amazing contributions.
It is also amazing when you start having a repertoire of answers, and as you are writing a new answer, you remember: "hey, the knowledge of that answer would be so welcome here", and so you link to the other answer as well at the perfect point. This somewhat achieves does what OurBigBook.com aims to do: for each small section of a tutorial, gather the best answers by multiple people.
Another one is Aaron Hall, who is also very high on the necromancer list, answers in Python which is a topic Ciro cares about, and states on his profile:so another necromancer.
Follow me on Twitter and tell me what canonical questions you would like me to respond to!
Way to go.
Ciro also asks some questions on a ratio of about 1 question per 10 answers. But Ciro's questions tend to be about extremely niche that no one knows/cares about, and a high percentage of them ends up getting self answered either at asking time or after later research.
Some fun reactions to Ciro's Stack Overflow activity:
- Eric B comments[ref] on Ciro's answer to the question "What does multicore assembly language look like?":
Holy shit, Ciro made it his masters degree to write OP an answer. What a long and detailed answer, thanks!
Ciro Santilli's Twitter accounts Updated 2025-07-16
Accounts controlled by Ciro Santilli on Twitter:
- twitter.com/cirosantilli primary channel, contains only updates on Ciro's best technical content. Low volume.
- twitter.com/cirosantilli2 secondary channel, contains smaller technical updates that didn't make it to the primary channel, and some China fun. Higher volume.
Ciro Santilli's wife Updated 2025-07-16
For more china-related stuff see: cirosantilli.com/china-dictatorship/wife
Excerpt of For Whom the Bell Tolls by Ernest Hemingway (1940), slightly adapted for brevity:Related: www.reddit.com/r/OldSchoolCool/comments/hj7bfq/comment/fwkik5v/
"Yes," the girl said. "Truly.""For you, Inglés?" Pilar looked at Robert Jordan. "Don't lie.""Yes," he said. "Truly."
Teresinha performed by Maria Bethânia
. Source. Composed and previously performed by Chico Buarque in 1987: Video "Teresinha by Chico Buarque".
This video has English subtitles, click CC to enable them. This is one of the the best popular Brazilian music (MPB) of all time. A transcribed English translation adapted slightly by Ciro Santilli to be a bit less literal:
The first one came to me as if coming from the flower shop
Brought a stuffed toy, brought an amethyst pin
He told me about his journey and the perks he had
He showed me his watch and called me 'queen'
He found me so undefended that he touched my heart
But he denied me nothing, so, frightened, I said 'no'The second came to me as if coming back from the bar
Brought a bottle of brandy too bitter to swallow
He asked me about my past and sniffed my food
He searched through my drawer and called me 'the lost one'
He found me so undefended that he scratched my heart
But he gave me nothing, so, frightened, I said 'no'
Song of pig by Xiangxiang (2005)
Source. Chinese: 猪之歌 by 香香. Baidu Baike page: baike.baidu.com/item/猪之歌/16181836. A dude wrote the lyrics though: 毛慧 (Mao Hui), but wouldn't have been a hit if he had performed it given the insane gender imbalance in China. Chinese lyrics on mojim: mojim.com/cny104491x1x1.htm. A quick translation:Pig, you have two holes in your nose, and they have snot when you catch a cold
Pig, you have dark eyes, you can't see the edge
Pig, your ears are so big, you can't hear me calling you stupid
Pig, your tail is curled and curled. It turns out that you can't live without it when you run and jump.Pig head, pig brain, pig body, pig tail, a wise toy who is never picky about food
Every day sleep until after three in the afternoon, you never brush your teeth, and you never fightPig, your belly is so bulging, you can tell at a glance that you can't stand the hardships of life
Pig, your skin is so white, you must have been from a rich family in your past life, oh
Legend has it that your ancestor had eight rakes, and it hit a peach blossom criminal.
When you see a beautiful girl, you chuckle, won't blush, and isn't afraid
Ciro's ASCII art circuit diagram notation Updated 2025-08-08
This notation is designed to be relatively easy to write. This is achieved by not drawing ultra complex ASCII art boxes of every component. It would be slightly more readable if we did that, but prioritizing the writer here.
Two wires are only joined if but the following are:
+ is given. E.g. the following two wires are not joined: |
--|--
| |
--+--
|Simple symmetric components:
-,+and|: wireAC: AC source. Parameters:e.g.:If only one side is given, the other is assumed to be at a groundAC_1Hz_2VG.C: capacitorG: ground. Often used together withDC, e.g.:means applying a voltage of 10 V across a 10 Ohm resistor, which would lead to a current of 1 ADC_10---R_10---GL: inductorMICROPHONE. As a multi-letter symmetric component, you can connect the two wires anywhere, e.g.or:---MICROPHONE---| MICROPHONE |SPEAKERR: resistorSQUID: SQUID deviceX: Josephson junction
Asymmetric components have multiple letters indicating different ports. The capital letter indicates the device, and lower case letters the ports. The wires then go into the ports:
D: diodeSample usage in a circuit:a: anode (where electrons can come in from)c: cathode
Can also be used vertically like aany other circuit:--aDc--We can also change the port order, the device is still the same due to capital| a D c |D:--cDa-- | Dac-- | Dca-- | --caDDCDC source. Ports:E.g. a 10 V source with a 10 Ohm resistor would be:p: positiven: negative
If only one side is given, the other is assumed to be at a the ground+---pDC_10_n---+ | | +----R_10------+G. We can also omitpandmin that case and assume thatpis the one used, e.g. the above would be equivalent to:If the voltage is not given, it is assumed to be a variable voltage power supply.DC_10---R_10---GLED: same as diodeI: electric current source. Ports:P: potentiometer source. Ports:1: one of the sides2: the middle3: the other side
T: transistor. The ports aresgTd:Sample usage in a circuit:s: sourceg: gated: gate
All the following are also equivalent:---+ | --sgTd--| g --sTd-- | --Tsgd-- |- ports can also be separated by double underscores from the component names to increase readability. Single underscores can also be used to increase readability of longer multi-word component names e.g.:which is the same as:
RPI_PICO_W__1gp0__3gnd | | R_2k | | | +-aLEDc-+represents a circuit linking port 1 of a Raspberry Pi Pico W, which is GPIO pin 0, through a resistor and an LED, back to pin 3 of the board, which is ground.RPI_PICO_W 1gp0 3gnd | | R_2k | | | +-aLEDc-+
Numbers characterizing components are put just next to each component with an underscore. When there is only one parameter, standard units are assumed, e.g.:means:Micro is denoted as
+-----+
| |
C_1p R_2k
| |
+-----+u. Ciro's everyone gets a raise story Updated 2025-07-16
Once upon a time, when Ciro worked at a company, one day the company decided to give everyone a 20% raise.
The likely reason was that Apple was coming to town, and was sucking the fuck out of the company's talent.
Nothing ever drove it so clearly into Ciro's heart the obvious fact that even for skilled jobs, companies don't pay you what you're worth. They pay you as little as possible so you won't quit to join someone else. It is pure market forces in play.
The annoying thing is that people are highly non-fungible, so much like painting auctions, you can only estimate your price by putting yourself on auction and seeing what people will pay for you, i.e. interviewing for new jobs.
Another point is that people have all sorts of stupid restrictions such as not wanting to work on certain areas for moral reasons, or not wanting to move away from a certain area they like. Companies will of course readily exploit such weakness to be able to pay less. Silly non-rational beings.
Cirq Updated 2025-07-16
Cisco Updated 2025-07-16
Nerds 2.0.1 excerpt about Cisco (1998)
Source. - youtu.be/mhz24AR3nIc?t=45 the founders both worked at Stanford University but because they were in different departments they couldn't send an email to one another.
- youtu.be/mhz24AR3nIc?t=54 Sandy Lerner is very nice and chilled. She says how she was amazed by Leonard's manners!
- youtu.be/mhz24AR3nIc?t=86 "sincerity begins at a little over 100 hours a week". The dude is a robot.
- youtu.be/mhz24AR3nIc?t=279 earthquake!!!
- youtu.be/d0ya8DggDYs?list=PLn7AqqWS1I_9EHEHy6sw-v6hUMhbeOTRW&t=3268 she bought a manor house, probably in Chawton Hampshire, England, possibly Chawton House
- youtu.be/d0ya8DggDYs?list=PLn7AqqWS1I_9EHEHy6sw-v6hUMhbeOTRW&t=3312 he started donating to search for extraterrestrial intelligence
There are unlisted articles, also show them or only show them.