Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Internal cross file references done right by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Examples of USA spying on its "allies" by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects OurBigBook.com vs X by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Other personal knowledge bases (Obsidian, static site generators, etc.), blogs, PDFs:
- no way to merge brains of multiple users
- some of them are not focused on publishing, only personal/internal company usage
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Edit and publish by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Topics: the best version of an article by other users (the killer feature) by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
The topics feature allows you to find the best version of a subject written by other users user
. Live demo: derivative. Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects What you get by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects An anonymous donor gave me 1000 Monero (~126,000 USD) on March 2024 to work on this for one year by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Motivation: university sucks real bad right now by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
The ultimate goal: create an university:
- without entry exams
- without course requirements
- where all material is free and available online: lecture notes, problem sheets, past exam papers
- where you only pay to take certification exams for the courses that you care about
The technical goal:
Get university students to write what they learn. All university material should be amazing and free!
The how:
Create the ultimate personal knowledge base software with multi-user mind-melding features.
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects I'm not a professional hacker, I did some very occasional OSINT just for fun by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Creative Commons CC By-SA by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
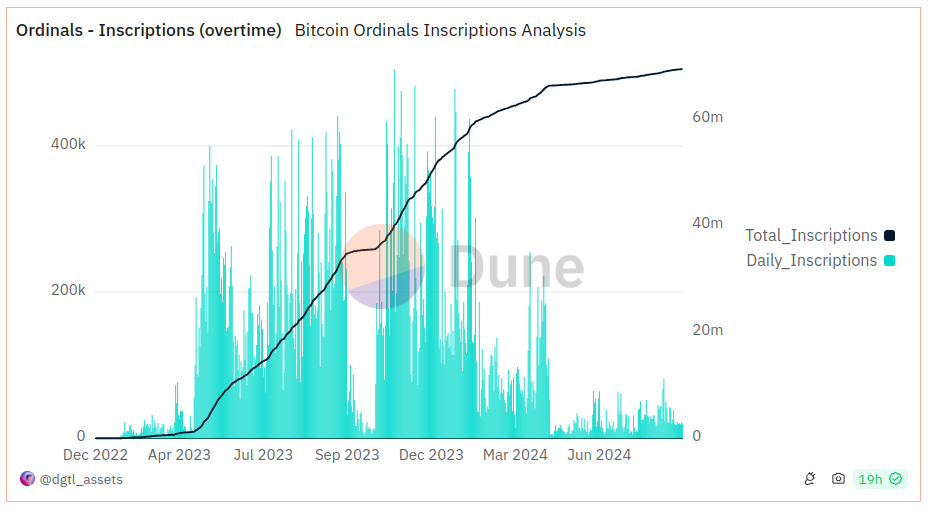
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Ordinal ruleset inscription (2022): the end of the line: Eternal September arrives by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects How illegal does something in the Bitcoin blockchain have to be to make it illegal? by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Methodology by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Coolest findings by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
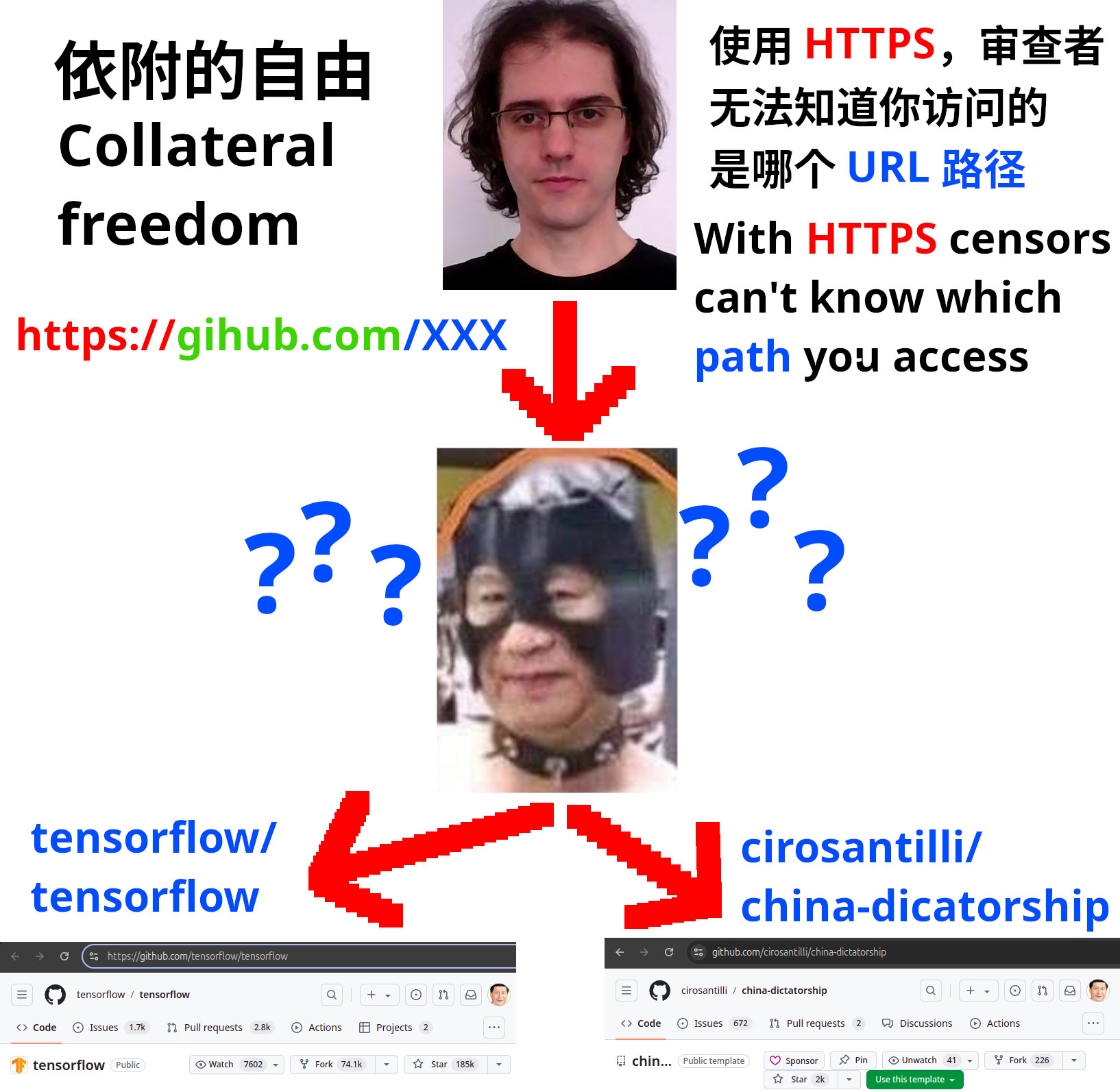
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Collateral freedom: HTTPS: the censor doesn't know which path you access by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Xi Jinping, sadomasochist in leather suit by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Xi Jinping, ruler of China, wearing leather sadomasochist outfit
. Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Xi Jinping, ruler of China by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Xi Jinping, ruler of China
. Aratu Week 2024 Talk by Ciro Santilli: My Best Random Projects Introduction by  Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
Ciro Santilli 40 Created 2024-09-06 Updated 2025-07-16
There are unlisted articles, also show them or only show them.









_Britons_(Kitchener)_wants_you_(Briten_Kitchener_braucht_Euch)._1914_(Nachdruck)%2C_74_x_50_cm._(Slg.Nr._552).jpg/401px-thumbnail.jpg)