Quantum computing is hard because we want long coherence but fast control by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
Mentioned e.g. at:
These are two conflicting constraints:
- long coherence times: require isolation from external world, otherwise observation destroys quantum state
- fast control and readout: require coupling with external world
English translation of papers that include the original Quantization as an Eigenvalue Problem by Schrödinger (1926).
But it's not something that he would do himself, unless under extreme cases.
Eugene's background: www.quora.com/Who-is-Eugene-Khutoryansky/answer/Ciro-Santilli
The frequency range of Wi-Fi, which falls in the microwave range, is likely chosen to allow faster data transfer than say, FM broadcasting, while still being relatively transparent to walls (though not as much).
It doesn't need to be a bipedal robot. We can let Boston Dynamics worry about that walking balance crap.
It could very well instead be on wheels like arm on tracks.
Or something more like a factory with arms on rails as per:
- Transcendence (2014)
- youtu.be/MtVvzJIhTmc?t=112 from Video "Rotrics DexArm is available NOW! by Rotrics (2020)" where they have a sliding rail
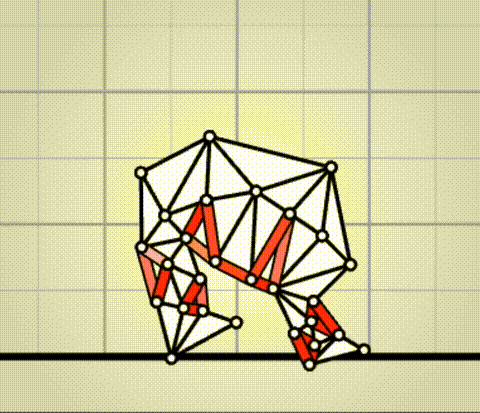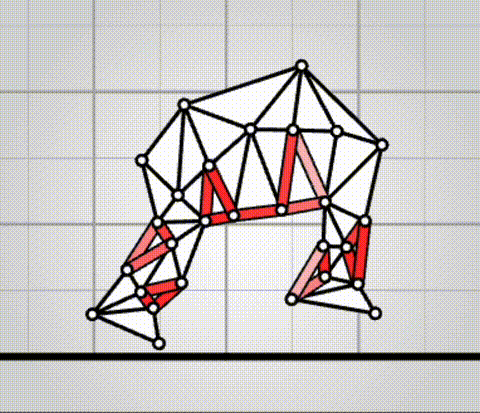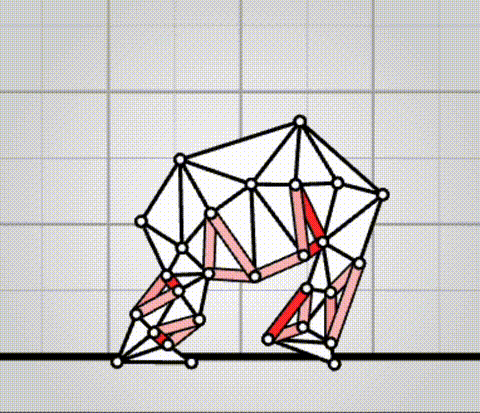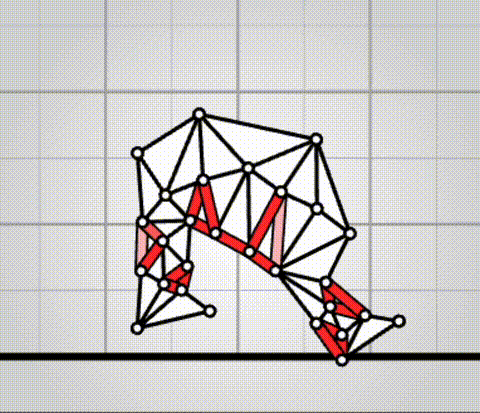
Algovivo demo
. github.com/juniorrojas/algovivo: A JavaScript + WebAssembly implementation of an energy-based formulation for soft-bodied virtual creatures.Although Ciro Santilli is a bit past their era, there's an aura of technical excellence about those people. It just seems that they sucked at business. Those open source hippies. Erm, wait.
Bibliography:
- archive.org/details/sunburstascentof00hall Sunburst: the ascent of Sun Microsystems by Mark Hall (1990)
Unlisted articles are being shown, click here to show only listed articles.