- HyperCard: we are kind of a "multiuser" version of HyperCard, trying to tie up cards made by different users. It is worth noting that HyperCard was one of the inspirations for WikiWikiWeb, which then inspired Wikipedia
- Semantic Web
- NLab
- physicstravelguide.com/ Nice manifesto: physicstravelguide.com/about by Jakob Schwichtenberg.
- OpenStax
- www.ft.com/content/5515ec3e-0040-4d90-85a9-df19d6e3ebd2 (archive) Twilio’s Jeff Lawson: an evangelist for software developersYou can never be first. But you can have the correct business model. That company's website must have gone into IP Purgatory, and could never be released as an open source website.As a student at the University of Michigan, he started a company that made lecture notes available free online, drawing a large audience of Midwestern college students and, soon enough, advertisers. At the height of the dotcom bubble, he dropped out of college, raised $10m from the venture firm Venrock and moved the company to Silicon Valley.His start-up drew interest from an acquirer that was planning to go public early in 2000. They closed the acquisition but missed their IPO window as the market plunged, and by August the company had filed for bankruptcy. Stock that Lawson and investors in his start-up received from the sale became worthless.He might actually be interested in donating to OurBigBook.com if it move forward now that he's a billionaire.
- Knol: basically the exact same thing by Google but 14 years earlier and declared a failure. Quite ominous:
- leanpub: similar goals, markdown-based, but the usual "you own your book copyright and you are trying to sell your book" approach
- nature Scitable
OK, just going random now:
The steps are sorted in roughly chronological order. The project might fail at any point, and some steps may be carried in parallel:
- create a basic implementation of the website, without advanced features like PageRank sorting and WYSIWYG. This is not much more than a blog with some extra metadata, so it is definitely achievable with constrained resources.
- Ciro would like to volunteer to work for free for this teacher and students to help the students learn.Ciro would start by mapping the headers of the lecture notes onto the website, and then slowly adding content as he feels the need to improve certain explanations.Finding teachers willing to allow this will be a major roadblock: how to convince teachers to use CC BY-SA.
- once some level of validation as been done, Ciro will start looking for charitable charitable grant opportunities more aggressively
- if things seem to be working, start adding more advance features: PageRank-like ranking sorting and WYSIWYG editingThe recommendation algorithms notably is left for a second stage because it needs real world data to be tested. And at the beginning, before Eternal September kicks in, there would be few posts written by well educated university students, so a simple sort by upvote would likely be good enough.
Ciro decided to start with a decent markup language with a decent implementation: OurBigBook Markup. Once that gets reasonable, he will move on to another attempt at the website itself.
The project description was originally at: github.com/cirosantilli/write-free-science-books-to-get-famous-website but being migrated here. The original working project name was "Write free books to get famous website", until Ciro decided to settle for
OurBigBook.com and fixed the domain name.The geometry of divisors is a topic in algebraic geometry that deals with the study of divisors on algebraic varieties, particularly within the context of the theory of algebraic surfaces and higher-dimensional varieties. A divisor on an algebraic variety is an algebraic concept that intuitively represents "subvarieties" or "subsets", often associated with codimension 1 subvarieties, such as curves on surfaces or hypersurfaces in higher dimensions.
Crush the current grossly inefficient educational system, replace today's students + teachers + researchers with unified "online content creators/consumers".
Gamify them, and pay the best creators so they can work it full time, until some company hires for more them since they are so provenly good.
Help create much greater equal opportunity to talented poor students as described at free gifted education.
Give the students a flexible choice of what to learn, which basically implies that a much large proportion of students get a de-facto gifted education.
In some ways, Ciro wants the website to feel like a video game, where you fluidly interact with headers, comments and their metadata. If game developers can achieve impressively complicated game engines, why can't we achieve a decent amazing elearning website? :-)
Related:
In this section we will gather some more advanced ideas besides the basic features described at how the website works.
It would be really cool to have a PageRank-link algorithm that answers the key questions:However, Ciro has decided to leave this for phase two action plan, because it is impossible to tune such an algorithm if you have no users or test data.
- what is the best content for subject X.For example, if you are reading
cirosantilli/riemann-integraland it is crap, you would be able to click the buttonwhich leads you to the URL: ourbigbook.com/subject/mathematics. This URL then contains a list of all pages people have written about the subjectVersions by other authors
mathematics, sorted by some algorithm, containing for example: - who knows the most about subject X. This can be found by visiting: ourbigbook.com/users/mathematics "Top Mathematics users", which would contain the list of users sorted by the algorithm:
Perhaps it is also worth looking into ExpertRank, they appear to do some kind of "expert in this area", but with clustering (unlike us, where the clustering would be more explicit).
Other dump of things worth looking into:
Ciro is looking for:
- university teachers who might be interested in trying it out as described at Section "Action plan", especially those who already use open licenses for their lecture notes
- funding possibilities for this project, including donations as mentioned at Section "Sponsor Ciro Santilli's work on OurBigBook.com" and contracts
The initial incentive for the creators is to make them famous and allow them to get more fulfilling jobs more easily, although Ciro also wants to add money transfer mechanisms to it later on.
We can't rely on teachers writing materials, because they simply don't have enough incentive: publication count is all that matters to their careers. The students however, are desperate to prove themselves to the world, and becoming famous for amazing educational content is something that some of them might want to spend their times on, besides grinding for useless grade.
OurBigBook.com Why it is hard to make money from this website by  Ciro Santilli 37 Updated 2025-07-16
Ciro Santilli 37 Updated 2025-07-16
There is basically only one scalable business model in education as of the 2020's: helping teenagers pass university entry exams. And nothing else. Everything else is a "waste" of time.
Perhaps there is a little bit of publicity incentive to helping them win knowledge olympiads as well, but it is tiny in comparison, and almost certainly not a scalable investment. This may also depend on whether universities consider anything but exams, which varies by country.
That marked is completely saturated, and Ciro Santilli refuses to participate in it for moral reasons.
Beyond that, there is no scalable investment. Other non-scalable investments that could allow one to make a lifestyle business are:
- extra-curricular initiatives to get younger children interested in science. These may have some money stream coming from the parents of the children. This happens because for young children, the parents are more in control, and the parents, unlike the students, have some money to spend. An example: www.littlehouseofscience.com/This business model is possible because experiments for young children may be cheap to realize, unlike any experiment that would matter to a teenager or adult.
- creating a private university, for profit or not. Of course, at this point, you would be either:
- competing against the reputation and funding of century old universities
- or be offering more boring, lower tech or techless courses, to (God forbid the phrasing) "worse students", i.e. at a "worse university"
Teenagers and young adults:
- don't have money to give you if you want to "help them learn for real"
- are somewhat forced to obtain their "reputable university" reputation to kickstart their careers
It is this perfect storm that places this specific section of education in such a bad shape that it is today.
This project is likely to fail. It could become the TempleOS of wikis. The project' autism score is quite high. It might be an impossible attempt at a lifestyle business. But Ciro is beyond caring now. It must be done. Other things that come to mind:
- www.youtube.com/playlist?list=PLibNZv5Zd0dzvoxXrjA9xNHLpdgLhTkZz "Obsessed" playlist by Wired. Helps Ciro feel better about himself.
- Don Quixote
- pipe dream
- Video "Don't Try - The Philosophy of Charles Bukowski by Pursuit of Wonder (2019)"
Dangerous combination:and for any crazy person who might wish to join: Men Wanted for Hazardous Journey.
In some ways, Ciro was reminded of OurBigBook.com by this documentary. Ken built his ultimate audio system without regard to money and time, to enjoy until he dies. Ciro is doing something similar. There is one fundamental difference however: everyone can enjoy a website all over the world.
A bit ominous though that the whole thing was eventually sold off for a fraction of the building cost: www.washingtonpost.com/style/interactive/2024/ken-fritz-greatest-stereo-auction-cost/.
Once the ball starts rolling, these are people who should be contacted.
Basically anything under educational charitable organization counts.
It is also worth having a look under the Wikipedia page for open educational resources: en.wikipedia.org/wiki/Open_educational_resources
Start with consulting for universities to get some cash flowing.
Help teachers create perfect courses.
Choose a domain of knowledge, generate perfect courses for it, and find all teachers of the domain in the world who are teaching that and help them out.
Then expand out to other domains.
TODO: which domain of knowledge should we go for? The more precise the better.
- maths is perfect because it "never" changes. But does not make money.
- computer science might be good, e.g. machine learning.
Teachers have the incentive of making open source to get more students.
Students pay when they want help to learn something.
Maybe focus on job ads like Stack Overflow.
Not a fun of giving up control for such a low-maintenance cost venture... but keeping a list just in case...
More info at: docs.ourbigbook.com#ourbigbook-web-topics
As mentioned at Section "Linux Kernel Module Cheat", this should be merged into that other project.
If Ciro Santilli weren't a natural born activist, he chould have made an excellent intelligence analyst! See also: Section "Being naughty and creative are correlated".
- Stack Overflow Vote Fraud Script
- GitHub makes Ciro feel especially naughty:
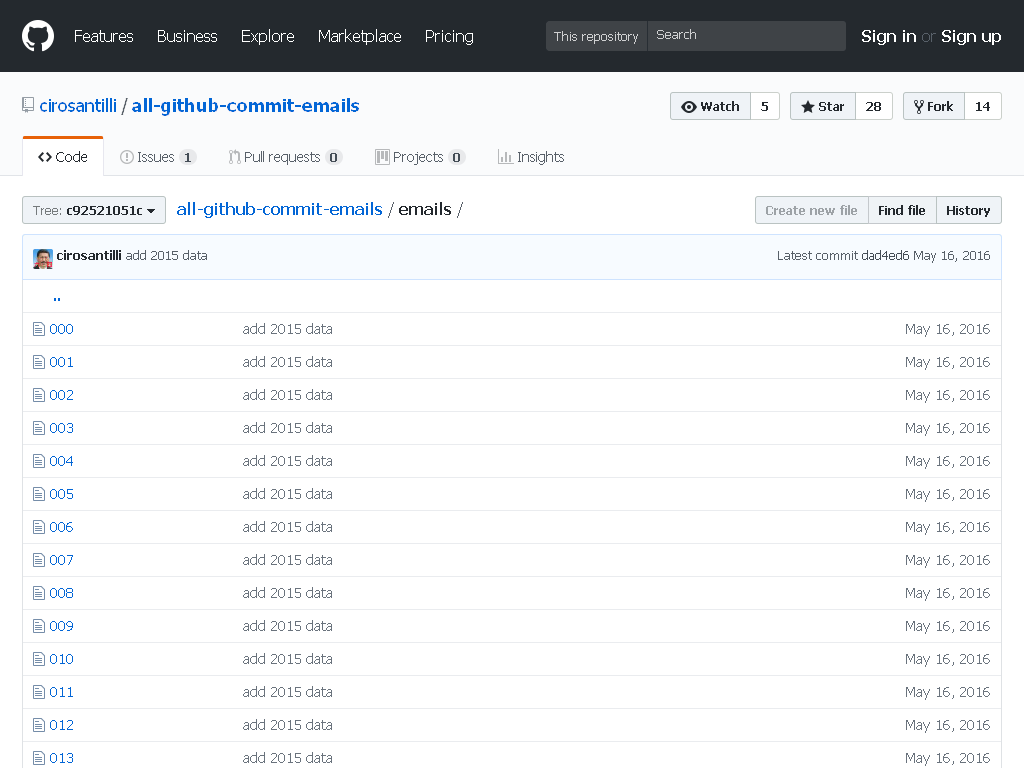
- All GitHub Commit Emails: he extracted (almost) all Git commit emails from GitHub with Google BigQuery
Figure 1. All GitHub Commit Emails repo before takedown. Screenshot from archive.is. - A repository with 1 million commits: likely the live repo with the most commits as of 2017
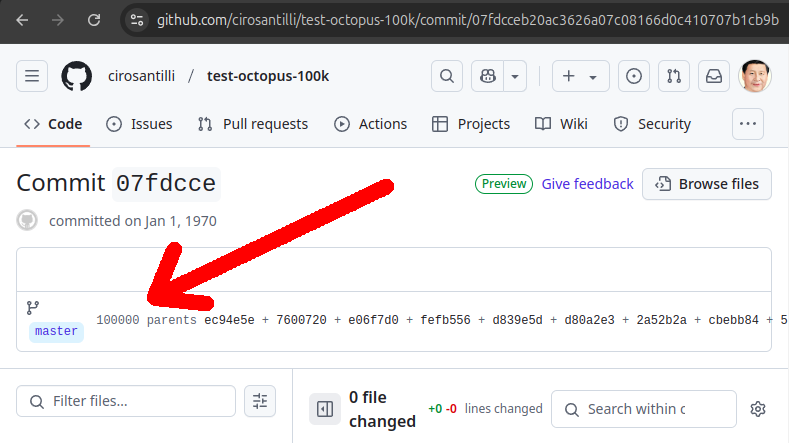
- An 100 year GitHub streak, likely longest ever when that existed. It was consuming too much server resources however, which led to GitHub admins manually turning off his contribution history.
Figure 3. Screenshot of a commit with 100k parents on GitHub. URL: github.com/cirosantilli/test-octopus-100k/commit/07fdcceb20ac3626a07c08166d0c410707b1cb9b- 500 on adoc infinite header xref recursion: that was fun while it lasted
Pinned article: Introduction to the OurBigBook Project
Welcome to the OurBigBook Project! Our goal is to create the perfect publishing platform for STEM subjects, and get university-level students to write the best free STEM tutorials ever.
Everyone is welcome to create an account and play with the site: ourbigbook.com/go/register. We belive that students themselves can write amazing tutorials, but teachers are welcome too. You can write about anything you want, it doesn't have to be STEM or even educational. Silly test content is very welcome and you won't be penalized in any way. Just keep it legal!
Intro to OurBigBook
. Source. We have two killer features:
- topics: topics group articles by different users with the same title, e.g. here is the topic for the "Fundamental Theorem of Calculus" ourbigbook.com/go/topic/fundamental-theorem-of-calculusArticles of different users are sorted by upvote within each article page. This feature is a bit like:
- a Wikipedia where each user can have their own version of each article
- a Q&A website like Stack Overflow, where multiple people can give their views on a given topic, and the best ones are sorted by upvote. Except you don't need to wait for someone to ask first, and any topic goes, no matter how narrow or broad
This feature makes it possible for readers to find better explanations of any topic created by other writers. And it allows writers to create an explanation in a place that readers might actually find it.Figure 1. Screenshot of the "Derivative" topic page. View it live at: ourbigbook.com/go/topic/derivativeVideo 2. OurBigBook Web topics demo. Source. - local editing: you can store all your personal knowledge base content locally in a plaintext markup format that can be edited locally and published either:This way you can be sure that even if OurBigBook.com were to go down one day (which we have no plans to do as it is quite cheap to host!), your content will still be perfectly readable as a static site.
- to OurBigBook.com to get awesome multi-user features like topics and likes
- as HTML files to a static website, which you can host yourself for free on many external providers like GitHub Pages, and remain in full control
Figure 3. Visual Studio Code extension installation.Figure 4. Visual Studio Code extension tree navigation.Figure 5. Web editor. You can also edit articles on the Web editor without installing anything locally.Video 3. Edit locally and publish demo. Source. This shows editing OurBigBook Markup and publishing it using the Visual Studio Code extension.Video 4. OurBigBook Visual Studio Code extension editing and navigation demo. Source. - Infinitely deep tables of contents:
All our software is open source and hosted at: github.com/ourbigbook/ourbigbook
Further documentation can be found at: docs.ourbigbook.com
Feel free to reach our to us for any help or suggestions: docs.ourbigbook.com/#contact