Bacteria Updated 2025-07-16
Bacterial cellular morphogology Updated 2025-07-16
Bacterial genome Updated 2025-07-16
Bad film Updated 2025-07-16
Banheiros da USP Updated 2025-07-16
Semi-comical student website to review the toilets of the University of São Paulo. Some of the toilets had a reputation for being terrible.
One is reminded of Crushbridge.
Barton Zwiebach Updated 2025-07-16
Affiliation: Massachusetts Institute of Technology.
Doctoral advisor: Murray Gell-Mann.
Based God Updated 2025-07-16
Someone who is not a pussy.
Someone once called Ciro Santilli that: archive.is/W1ocv. It's an overstatement, considering that Ciro's parents have some money. Not infinite. But still. Changes everything. A real Based God is someone like Charles Bukowski, who had to work decades at the post office.
BCS Theory Updated 2025-07-16
Main theory to explain Type I superconductors very successfully.
TODO can someone please just give the final predictions of BCS, and how they compare to experiments, first of all? Then derive them.
High level concepts:
- the wave functions of pairs of electrons (fermions) get together to form bosons. This is a phase transition effect, thus the specific sudden transition temperature.
- the pairs form a Bose-Einstein condensate
- once this new state is reached, all pairs are somehow entangled into one big wave function, and you so individual lattice imperfections can't move just one single electron off trajectory and make it lose energy
Beeching cuts Updated 2025-07-16
Bibliograpy:
- Losing Track by Channel 4 (1984), especially episode 5
- www.theguardian.com/uk/2013/mar/02/beeching-wrong-about-britains-railwaysToday the makeup of UK transport looks very different from the one envisaged by Dr Beeching. Rail passenger figures have almost doubled over the past 10 years; commuter trains are crammed; young people are deserting the car for the train; and Britain's railway bosses are struggling to meet soaring demands for seats. The legacy of Beeching - dug-up lines, sold-off track beds and demolished bridges - has only hindered plans to revitalise the network, revealing the dangers of having a single, inflexible vision when planning infrastructure."The crucial lesson to take from the Beeching anniversary is that you have to be flexible when planning transport infrastructure. Beeching was not," says Colin Divall, professor of rail history at York University. "Yes, many loss-making lines did need closing down, but nowhere near the number earmarked by Beeching, as we can now see with terrible hindsight."
Lagrangian density Updated 2025-07-16
In the case of field however, we can expand the Lagrangian out further, to also integrate over the space coordinates and their derivatives.
Since we are now working with something that gets integrated over space to obtain the total action, much like density would be integrated over space to obtain a total mass, the name "Lagrangian density" is fitting.
Of course, if we were to write it like that all the time we would go mad, so we can just write a much more condensed vectorized version using the gradient with :
And in the context of special relativity, people condense that even further by adding to the spacetime Four-vector as well, so you don't even need to write that separate pesky .
The main point of talking about the Lagrangian density instead of a Lagrangian for fields is likely that it treats space and time in a more uniform way, which is a basic requirement of special relativity: we have to be able to mix them up somehow to do Lorentz transformations. Notably, this is a key ingredient in a/the formulation of quantum field theory.
Lagrangian vs Hamiltonian Updated 2025-07-16
The key difference from Lagrangian mechanics is that the Hamiltonian approach groups variables into pairs of coordinates called the phase space coordinates:This leads to having two times more unknown functions than in the Lagrangian. However, it also leads to a system of partial differential equations with only first order derivatives, which is nicer. Notably, it can be more clearly seen in phase space.
- generalized coordinates, generally positions or angles
- their corresponding conjugate momenta, generally velocities, or angular velocities
Laplace's equation Updated 2025-07-16
TODO confirm: does the solution of the heat equation always converge to the solution of the Laplace equation as time tends to infinity?
In one dimension, the Laplace equation is boring as it is just a straight line since the second derivative must be 0. That also matches our intuition of the limit solution of the heat equation.
Largest known ranks of an elliptic curve over the rational numbers Updated 2025-07-16
web.math.pmf.unizg.hr/~duje/tors/rankhist.html gives a list with Elkies (2006) on top with:TODO why this non standard formulation?
Elliptic curve Updated 2025-07-16
An elliptic curve is defined by numbers and . The curve is the set of all points of the real plane that satisfy the Equation 1. "Definition of the elliptic curves"
Equation 1.
Definition of the elliptic curves
. Equation 1. "Definition of the elliptic curves" definies elliptic curves over any field, it doesn't have to the real numbers. Notably, the definition also works for finite fields, leading to elliptic curve over a finite fields, which are the ones used in Elliptic-curve Diffie-Hellman cyprotgraphy.
Being naughty and creative are correlated Updated 2025-07-16
Largey Brage Updated 2025-07-16
Both of them attended Montessori education at some point. Interesting! Mentioned in a talk by Sergey and highlighted at The Google Story.
They stepped down from leading Google roles in 2019: www.npr.org/2019/12/03/784570156/google-founders-brin-page-step-down-pichai-takes-over-as-alphabet-ceo
As The Google Story puts it about Largey:Ciro Santilli likes that.
Scholarship was not just emphasized in their homes; it was treasured.
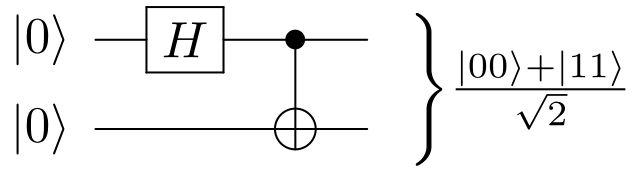
Bell circuit Updated 2025-07-16
Bell Labs Holmdel Complex Updated 2025-07-16
101 Crawfords Corner Rd Holmdel, NJ 07733 USA
They had a smaller building first: youtu.be/BPq_ZyOvbsg?t=51 and in 1962 opened the large new building.
Bell Labs Murray Hill Updated 2025-07-16
Became headquarters in 1967,
Drone footage: www.youtube.com/watch?v=z0Ld2KFjaC8 Bell LABS Headquarters Murray Hill NJ in 4K Drone Flight by ESTOUCHFPV (2017)
Notable inventions made there:
- the first transistor
- TODO confirm C
Bell test experiment Updated 2025-07-16
Some of the most remarkable ones seem to be:
- Alain Aspect 1982
- Hensen et al., Giustina et al., Shalm et al. (2015): "loophole-free" Bell tests
Unlisted articles are being shown, click here to show only listed articles.