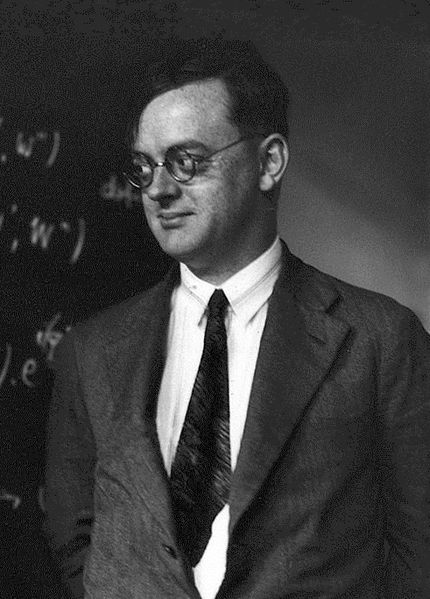Human body Updated 2025-07-16
Pascual Jordan Updated 2025-07-16
One of the leading figures of the early development of quantum electrodynamics.
Philip W. Anderson Updated 2025-07-16
University of California, Santa Barbara Updated 2025-07-16
Transhumanism Updated 2025-07-16
University of Cambridge lecture note copyright ownership Updated 2025-07-16
Teachers appear to own it, just allowing perpetual non exclusive rights to university: www.admin.cam.ac.uk/univ/so/pdfs/2022/ordinance13.pdf
30. In relation to teaching materials prepared by a University staff member for use in the teaching primarily of the University’s students, unless the Faculty Board or other body responsible for teaching has agreed explicitly to the contrary, the University shall have a non-exclusive, royalty-free, perpetual license to use the material for teaching in the University.
University of London Updated 2025-07-16
University of Paris Updated 2025-07-16
Their split in 1970 was a huge fuck up. If it were a single entity, the university would likely be in the top 10 university rankings, undoubtedly top 20. But as of 2020 French universities only appear instead in the top 40s or 50s.
Indian classical music trope type Updated 2025-07-16
Instant messaging vs email Updated 2025-07-16
University of São Paulo Updated 2025-07-16
In retrospect, doing electrical engineering (and likey the other engineering degrees) felt like taking a trip to the 60s in the United States, due to both the subject matter, and how old the concrete buildings were!
This does not need to be a bad thing. It is in that era (and earlier) that much of the exciting foundations of the field were set, and there is great value in there is value in tutorials written by early pioneers of the field. Not that they were amazing at excting history lessons as they should be. But the course outline suggested that intent.
But that point of view must also be accompanied by the excitement of the great ongoing advances of technology (and impact they had in the past). And on that, they failed.
University of the People Updated 2025-07-16
Online and free. Pay only for exams, i.e. exam as a service. Almost perfect according to Ciro Santilli's idea.
E91 Updated 2025-07-16
Requires entangled particles, unlike BB84 which does not.
Intelligence Updated 2025-07-16
Organization developing quantum hardware Updated 2025-07-16
Prime k-tuple conjecture Updated 2025-07-16
There are infinitely many prime k-tuples for every admissible tuple.
Generalization of the Twin prime conjecture.
Prize Updated 2025-07-16
Generally, prizes that pay big lumps of money to well established individuals are a bit useless, it would be better to pay smaller sums to struggling beginners in the field, of which there are aplenty.
The most important part about prizes should not be the money, nor the recognition, but rather explaining better what the laureates did. In this, most prizes fail. Thus Ciro Santilli's project idea: Project to explain each Nobel Prize better.
Quantum computing university course Updated 2025-07-16
Quantum programming framework Updated 2025-07-16
Unlisted articles are being shown, click here to show only listed articles.