Ciro Santilli @cirosantilli 35

This is not a truly "fundamental" constant of nature like say the speed of light or the Planck constant.

Rather, it is just a definition of our Kelvin temperature scale, linking average microscopic energy to our macroscopic temperature scale.

The way to think about that link is, at 1 Kelvin, each particle has average energy:per degree of freedom.

This is why the units of the Boltzmann constant are Joules per Kelvin.

For an ideal monatomic gas, say helium, there are 3 degrees of freedom. so each helium atom has average energy:

If we have 2 atoms at 1 K, they will have average energy $6/2k_{B}J$, and so on.

Another conclusion is that this defines temperature as being proportional to the total energy. E.g. if we had 1 helium atom at 2 K then we would have about $6/2k_{B}J$ energy, 3 K $9/2k_{B}J$ and so on.

This energy is of course just an average: some particles have more, and others less, following the Maxwell-Boltzmann distribution.

An alloy of iron and carbon. Because such allys have had such incredible historical importance due to their different properties, different phases of Fe-C have well known names such as steel

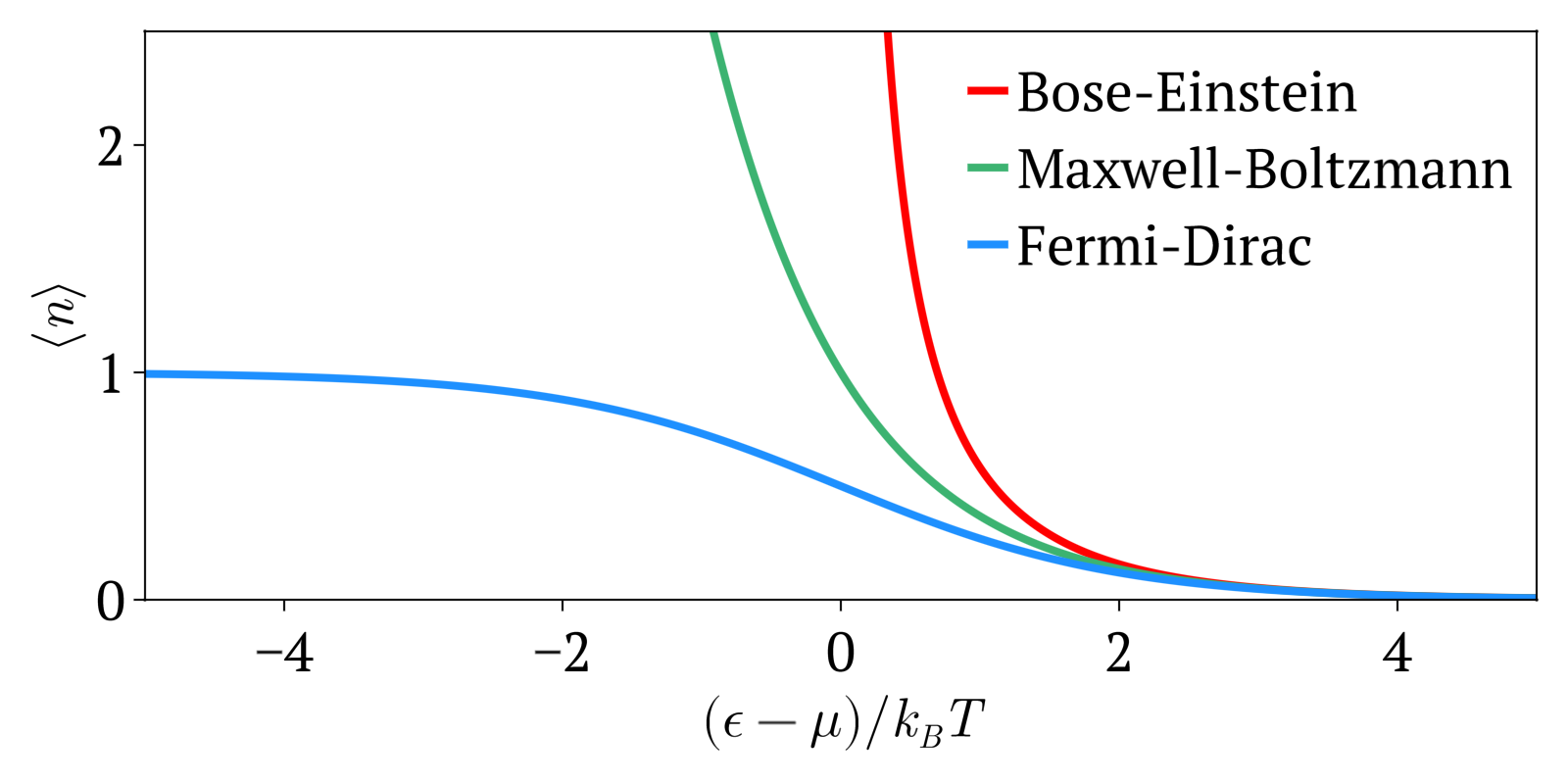
Maxwell-Boltzmann statistics, Bose-Einstein statistics and Fermi-Dirac statistics all describe how energy is distributed in different physical systems at a given temperature.

For example, Maxwell-Boltzmann statistics describes how the speeds of particles are distributed in an ideal gas.

The temperature of a gas is only a statistical average of the total energy of the gas. But at a given temperature, not all particles have the exact same speed as the average: some are higher and others lower than the average.

For a large number of particles however, the fraction of particles that will have a given speed at a given temperature is highly deterministic, and it is this that the distributions determine.

One of the main interest of learning those statistics is determining the probability, and therefore average speed, at which some event that requires a minimum energy to happen happens. For example, for a chemical reaction to happen, both input molecules need a certain speed to overcome the potential barrier of the reaction. Therefore, if we know how many particles have energy above some threshold, then we can estimate the speed of the reaction at a given temperature.

The three distributions can be summarized as:

A good conceptual starting point is to like the example that is mentioned at The Harvest of a Century by Siegmund Brandt (2008).

Consider a system with 2 particles and 3 states. Remember that:

Therefore, all the possible way to put those two particles in three states are for:

Ciro Santilli once visited the chemistry department of a world leading university, and the chemists there were obsessed with NMR. They had small benchtop NMR machines. They had larger machines. They had a room full of huge machines. They had them in corridors and on desk tops. Chemists really love that stuff. More precisely, these are used for NMR spectroscopy, which helps identify what a sample is made of.

Basically measures the concentration of certain isotopes in a region of space.