Incoming links: Fermion
Key physical experiment: fractional quantum Hall effect.
The name actually comes from "any". Amazing.
All known anyons are quasiparticles.
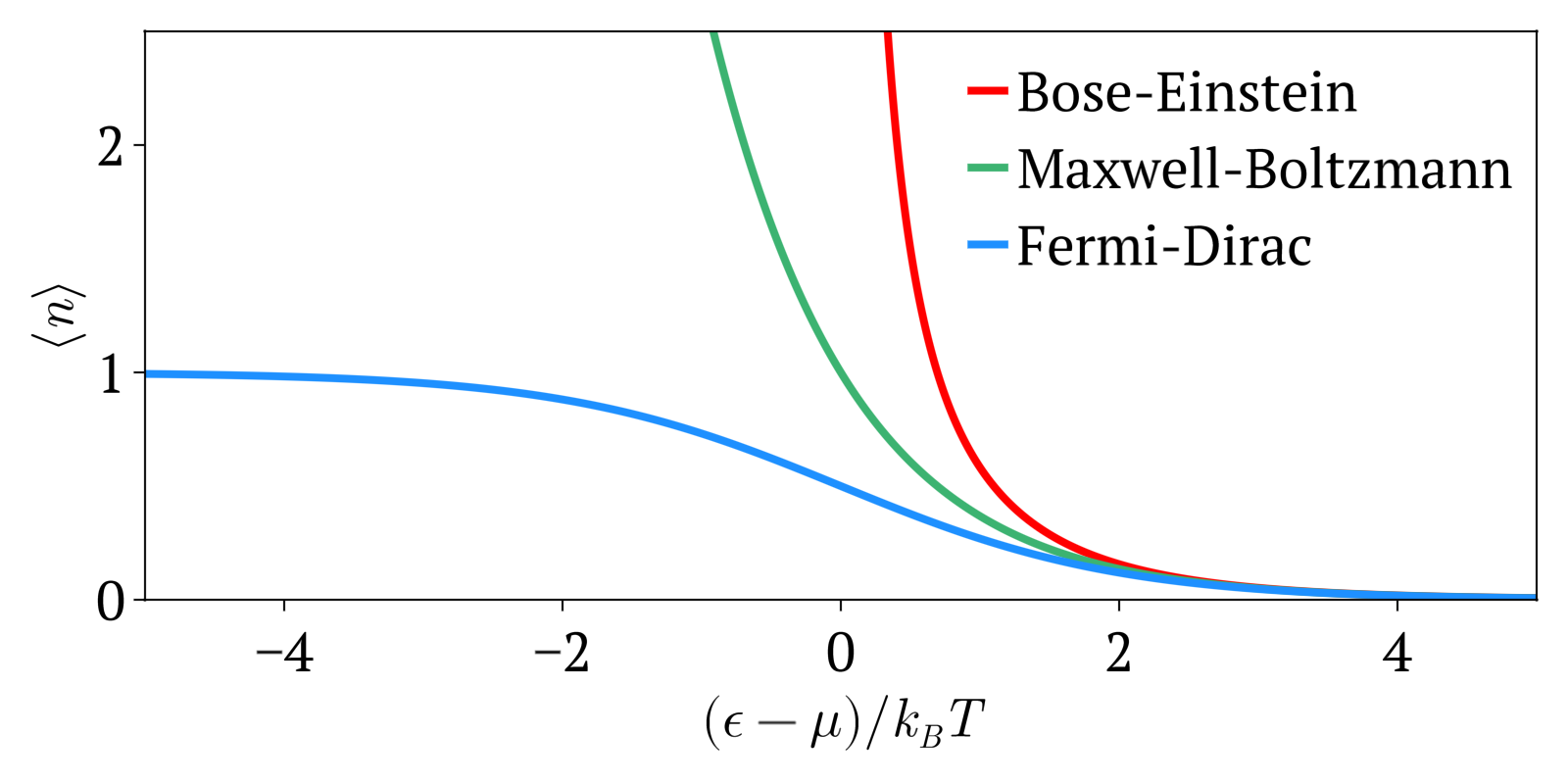
Maxwell-Boltzmann vs Bose-Einstein vs Fermi-Dirac statistics Updated 2024-12-15 +Created 2024-10-28
Maxwell-Boltzmann statistics, Bose-Einstein statistics and Fermi-Dirac statistics all describe how energy is distributed in different physical systems at a given temperature.
For example, Maxwell-Boltzmann statistics describes how the speeds of particles are distributed in an ideal gas.
The temperature of a gas is only a statistical average of the total energy of the gas. But at a given temperature, not all particles have the exact same speed as the average: some are higher and others lower than the average.
For a large number of particles however, the fraction of particles that will have a given speed at a given temperature is highly deterministic, and it is this that the distributions determine.
One of the main interest of learning those statistics is determining the probability, and therefore average speed, at which some event that requires a minimum energy to happen happens. For example, for a chemical reaction to happen, both input molecules need a certain speed to overcome the potential barrier of the reaction. Therefore, if we know how many particles have energy above some threshold, then we can estimate the speed of the reaction at a given temperature.
The three distributions can be summarized as:
- Maxwell-Boltzmann statistics: statistics without considering quantum statistics. It is therefore only an approximation. The other two statistics are the more precise quantum versions of Maxwell-Boltzmann and tend to it at high temperatures or low concentration. Therefore this one works well at high temperatures or low concentrations.
- Bose-Einstein statistics: quantum version of Maxwell-Boltzmann statistics for bosons
- Fermi-Dirac statistics: quantum version of Maxwell-Boltzmann statistics for fermions. Sample system: electrons in a metal, which creates the free electron model. Compared to Maxwell-Boltzmann statistics, this explained many important experimental observations such as the specific heat capacity of metals. A very cool and concrete example can be seen at youtu.be/5V8VCFkAd0A?t=1187 from Video "Using a Photomultiplier to Detect single photons by Huygens Optics" where spontaneous field electron emission would follow Fermi-Dirac statistics. In this case, the electrons with enough energy are undesired and a source of noise in the experiment.
Maxwell-Boltzmann vs Bose-Einstein vs Fermi-Dirac statistics
. Source. 
A good conceptual starting point is to like the example that is mentioned at The Harvest of a Century by Siegmund Brandt (2008).
Consider a system with 2 particles and 3 states. Remember that:
- in quantum statistics (Bose-Einstein statistics and Fermi-Dirac statistics), particles are indistinguishable, therefore, we might was well call both of them
A, as opposed toAandBfrom non-quantum statistics - in Bose-Einstein statistics, two particles may occupy the same state. In Fermi-Dirac statistics
Therefore, all the possible way to put those two particles in three states are for:
- Maxwell-Boltzmann distribution: both A and B can go anywhere:
State 1 State 2 State 3 AB AB AB A B B A A B B A A B B A - Bose-Einstein statistics: because A and B are indistinguishable, there is now only 1 possibility for the states where A and B would be in different states.
State 1 State 2 State 3 AA AA AA A A A A A A - Fermi-Dirac statistics: now states with two particles in the same state are not possible anymore:
State 1 State 2 State 3 A A A A A A
Bibliography review:
- Quantum Field Theory lecture notes by David Tong (2007) is the course basis
- quantum field theory in a nutshell by Anthony Zee (2010) is a good quick and dirty book to start
Course outline given:
- classical field theory
- quantum scalar field. Covers bosons, and is simpler to get intuition about.
- quantum Dirac field. Covers fermions
- interacting fields
- perturbation theory
- renormalization
Non-relativistic QFT is a limit of relativistic QFT, and can be used to describe for example condensed matter physics systems at very low temperature. But it is still very hard to make accurate measurements even in those experiments.
Defines "relativistic" as: "the Lagrangian is symmetric under the Poincaré group".
Mentions that "QFT is hard" because (a finite list follows???):But I guess that if you fully understand what that means precisely, QTF won't be too hard for you!
There are no nontrivial finite-dimensional unitary representations of the Poincaré group.
Notably, this is stark contrast with rotation symmetry groups (SO(3)) which appears in space rotations present in non-relativistic quantum mechanics.
www.youtube.com/watch?v=T58H6ofIOpE&t=5097 describes the relativistic particle in a box thought experiment with shrinking walls
Surprisingly, it can also become a superfluid even though each atom is a fermion! This is because of Cooper pair formation, just like in superconductors, but the transition happens at lower temperatures than superfluid helium-4, which is a boson.
aps.org/publications/apsnews/202110/history.cfm: October 1972: Publication of Discovery of Superfluid Helium-3 contains comments on the seminal paper and a graph which we must steal.