It is a bit hard to decide if those people are serious or not. Sometimes it feels scammy, but sometimes it feels fun and right!
Particularly concerning is the fact that they are not a not-for-profit entity, and it is hard to understand how they might make money.
Charles Simon, the founder, is pretty focused in how natural neurons work vs artificial neural network models. He has some good explanations of that, and one major focus of the project is their semi open source spiking neuron simulator BrainSimII. While Ciro Santilli believes that there might be insight in that, he also has doubts if certain modules of the brain wouldn't be more suitable coded directly in regular programming languages with greater ease and performance.
FutureAI appears to be Charles' retirement for fun project, he is likely independently wealthy. Well done.
- www.aitimejournal.com/interview-with-charles-simon-ceo-and-founder-futureai
- 2022 raised 2 million USD:
Creativity and AGI by Charles Simon's at AGI-22 (2022)
Source. Sounds OK!- youtu.be/ivbGbSx0K8k?t=856 general structure of the human brain 86B total, matching number of neurons in the human brain, with:
- 14B: brainstem
- 16B: neocortex
- 56B: cerebelum
- www.youtube.com/watch?t=1433 some sequencing ideas/conjectures
Machine Learning Is Not Like Your Brain by Future AI (2022)
Source. Contains some BrainSimII demos.For some reason, Ciro Santilli is mildly obsessed with understanding and visualizing the real projective plane.
To see why this is called a plane, move he center of the sphere to , and project each line passing on the center of the sphere on the x-y plane. This works for all points of the sphere, except those at the equator . Those are the points at infinity. Note that there is one such point at infinity for each direction in the x-y plane.
It good to think about how Euclid's postulates look like in the real projective plane:
- Since there is one point of infinity for each direction, there is one such point for every direction the two parallel lines might be at. The parallel postulate does not hold, and is replaced with a simpler more elegant version: every two lines meet at exactly one point.One thing to note however is that ther real projective plane does not have angles defined on it by definition. Those can be defined, forming elliptic geometry through the projective model of elliptic geometry, but we can interpret the "parallel lines" as "two lines that meet at a point at infinity"
- points in the real projective plane are lines in
- lines in the real projective plane are planes in .For every two projective points there is a single projective line that passes through them.Note however that not all lines in the real plane correspond to a projective line: only lines tangent to a circle at zero do.
Unlike the real projective line which is homotopic to the circle, the real projective plane is not homotopic to the sphere.
The topological difference bewteen the sphere and the real projective space is that for the sphere all those points in the x-y circle are identified to a single point.
One more generalized argument of this is the classification of closed surfaces, in which the real projective plane is a sphere with a hole cut and one Möbius strip glued in.
Ciro Santilli's preferred visualization of the real projective plane is a small variant of the standard "lines through origin in ".
For those sphere points in the circle on the x-y plane, you should think of them as magic poins that are identified with the corresponding antipodal point, also on the x-y, but on the other side of the origin. So basically you you can teleport from one of those to the other side, and you are still in the same point.
Ciro likes this model because then all the magic is confined just to the part of the model, and everything else looks exactly like the sphere.
It is useful to contrast this with the sphere itself. In the sphere, all points in the circle are the same point. But this is not the case for the projective plane. You cannot instantly go to any other point on the by just moving a little bit, you have to walk around that circle.
Spherical cap model of the real projective plane
. On the x-y plane, you can magically travel immediately between antipodal points such as A/A', B/B' and C/C'. Or equivalently, those pairs are the same point. Every other point outside the x-y plane is just a regular point like a normal sphere.The 3D regular convex polyhedrons are super famous, have the name: Platonic solid, and have been known since antiquity. In particular, there are only 5 of them.
The counts per dimension are:
The cool thing is that the 3 that exist in 5+ dimensions are all of one of the three families:Then, the 2 3D missing ones have 4D analogues and the sixth one in 4D does not have a 3D analogue: the 24-cell. Yes, this is the kind of irregular stuff Ciro Santilli lives for.
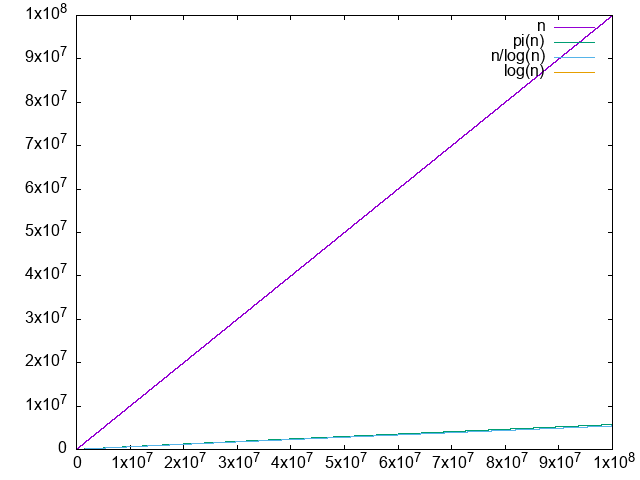
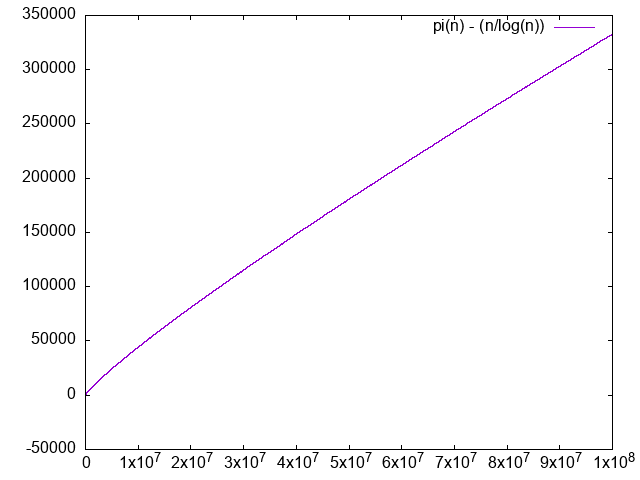
Consider this is a study in failed computational number theory.
The approximation converges really slowly, and we can't easy go far enough to see that the ration converges to 1 with only awk and primes:Runs in 30 minutes tested on Ubuntu 22.10 and P51, producing:
sudo apt intsall bsdgames
cd prime-number-theorem
./main.py 100000000. It is clear that the difference diverges, albeit very slowly.
. We just don't have enough points to clearly see that it is converging to 1.0, the convergence truly is very slow. The logarithm integral approximation is much much better, but we can't calculate it in awk, sadface.
But looking at: en.wikipedia.org/wiki/File:Prime_number_theorem_ratio_convergence.svg we see that it takes way longer to get closer to 1, even at it is still not super close. Inspecting the code there we see:so OK, it is not something doable on a personal computer just like that.
(* Supplement with larger known PrimePi values that are too large for \
Mathematica to compute *)
LargePiPrime = {{10^13, 346065536839}, {10^14, 3204941750802}, {10^15,
29844570422669}, {10^16, 279238341033925}, {10^17,
2623557157654233}, {10^18, 24739954287740860}, {10^19,
234057667276344607}, {10^20, 2220819602560918840}, {10^21,
21127269486018731928}, {10^22, 201467286689315906290}, {10^23,
1925320391606803968923}, {10^24, 18435599767349200867866}};Do as I say, not as I do: Ciro Santilli's Stack Overflow suspension for vote fraud script 2019, meta.stackoverflow.com/questions/381577/is-it-ok-to-have-links-on-how-to-create-sock-puppets-and-gain-rep-fraudulently-i/381635#381635.
LockPickingLawyer SAINTCON keynote (2021)
Source. SAINTCON is "Utah's Premiere Security Conference".- youtu.be/IH0GXWQDk0Q?t=900 mentions that Alfred Charles Hobbs commented in 1853:
Rogues are very keen in their profession, and know already much more than we can teach them
"Multicategory" can refer to multiple concepts depending on the context in which it's used. Here are a few common interpretations: 1. **Multicategory Classification**: In machine learning and statistics, multicategory classification (also known as multiclass classification) refers to a type of problem where a model needs to classify instances into more than two categories or classes.
Pinned article: Introduction to the OurBigBook Project
Welcome to the OurBigBook Project! Our goal is to create the perfect publishing platform for STEM subjects, and get university-level students to write the best free STEM tutorials ever.
Everyone is welcome to create an account and play with the site: ourbigbook.com/go/register. We belive that students themselves can write amazing tutorials, but teachers are welcome too. You can write about anything you want, it doesn't have to be STEM or even educational. Silly test content is very welcome and you won't be penalized in any way. Just keep it legal!
Intro to OurBigBook
. Source. We have two killer features:
- topics: topics group articles by different users with the same title, e.g. here is the topic for the "Fundamental Theorem of Calculus" ourbigbook.com/go/topic/fundamental-theorem-of-calculusArticles of different users are sorted by upvote within each article page. This feature is a bit like:
- a Wikipedia where each user can have their own version of each article
- a Q&A website like Stack Overflow, where multiple people can give their views on a given topic, and the best ones are sorted by upvote. Except you don't need to wait for someone to ask first, and any topic goes, no matter how narrow or broad
This feature makes it possible for readers to find better explanations of any topic created by other writers. And it allows writers to create an explanation in a place that readers might actually find it.Figure 1. Screenshot of the "Derivative" topic page. View it live at: ourbigbook.com/go/topic/derivativeVideo 2. OurBigBook Web topics demo. Source. - local editing: you can store all your personal knowledge base content locally in a plaintext markup format that can be edited locally and published either:This way you can be sure that even if OurBigBook.com were to go down one day (which we have no plans to do as it is quite cheap to host!), your content will still be perfectly readable as a static site.
- to OurBigBook.com to get awesome multi-user features like topics and likes
- as HTML files to a static website, which you can host yourself for free on many external providers like GitHub Pages, and remain in full control
Figure 2. You can publish local OurBigBook lightweight markup files to either OurBigBook.com or as a static website.Figure 3. Visual Studio Code extension installation.Figure 5. . You can also edit articles on the Web editor without installing anything locally. Video 3. Edit locally and publish demo. Source. This shows editing OurBigBook Markup and publishing it using the Visual Studio Code extension. - Infinitely deep tables of contents:
All our software is open source and hosted at: github.com/ourbigbook/ourbigbook
Further documentation can be found at: docs.ourbigbook.com
Feel free to reach our to us for any help or suggestions: docs.ourbigbook.com/#contact