This section contains some of the most interesting and a few representative screenshots of the websites found.
We intentionally omit the screenshots already reported by the Reuters article.
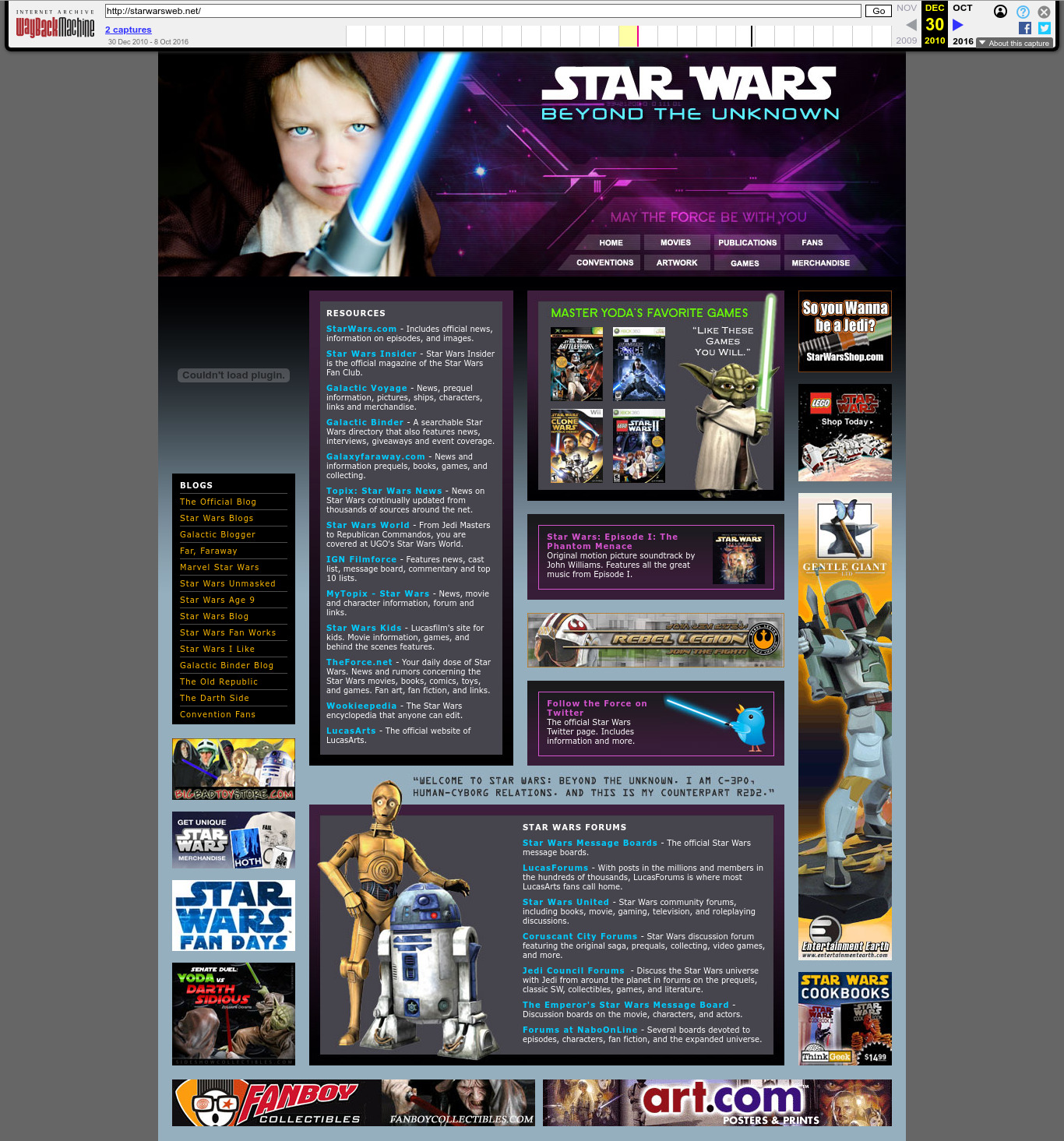
2010 Wayback Machine archive of starwarsweb.net
. The Star Wars one. Clearly branded websites like this are rare, which makes finding them all the much more fun. The Reuters article had two of them (Carson and rastadirect.net), so these were probably manually selected from the full hit dataset, and did not serve specifically as entry points. Most of the websites are quite boring and forgetful as you'd expect.
The subtitle "Beyond The Unknown" may be a reference to the Unknown Regions, an unexplored area of the galaxy in the Star Wars fictional universe.
The photo can still be licensed today as of 2025: www.gettyimages.co.uk/detail/photo/little-jedi-royalty-free-image/172984439. We found it by searching for "jedi boy" on gettyimages.co.uk. The photo is credited to a
madisonwi, presumably an alias based on the location Madison, Wisconsin. Here's a random website about adoption that uses it: www.adoptionadvocates.net/star-wars-adoption-language/ and where it can be seen without the watermarks.It later ocurred to Ciro Santilli that perhaps Reuters chose not to showcase this website because it features the photograph of a minor. But Ciro is sure that that minor is now a handsome young man in his 20's and would find the entire story very amusing if he ever finds out about it!
The images of the droids can be seen e.g. at: www.amazon.co.uk/04-Kampf-Droiden-Superheftig-Jedi/dp/B004TINSW6, a promotional material for a 2008 The Clone Wars television series audio CD and available as transparent PNGs without background in several sources. The Yoda art also seems to come from that show: rpggamer.org/page.php?page=4229.
One can almost picture the contractor who made that site seeing his children watching that show or playing the video game one evening, when a lightbulb popped over their head: tomorrow I'm going to have some fun at work.
In retrospect however, this website was likely a bad idea, since the massive pop culture appeal of Star Wars meant that when The CIA Secretly Ran a Star Wars Fan Site by Joseph Cox was published in 2025 the combination of "CIA" and "Star Wars" on a single sentence produced an irresistible clickbait that amplified knowledge of the fiasco to general public in a way that poor Johnny Carson and Bob Marley could never do. That's why you just can't have fun while working for the secret services anymore.
2011 Wayback Machine archive of alljohnny.com
. Source. Although alljohnny.com is one of the original Reuters examples, we are highlighting this screenshot here because the Reuters provided screenshot is from the extremely early 2004 version of the site, and it is interesting to see how this unique example was later updated in this 2011 version, the only known such case so far. The lack of OPSEC awareness is mind blowing, them reusing a domain like that after so many years in a completely new threat environment and possibly for a new asset.2011 Wayback Machine archive of webofcheer.com scrolled to show Johnny Carson
. Source. This website is a fansite for various comedians. It is the second known reference to Johnny Carson after alljohnny.com, which was one of the original screenshots given in the Reuters article. There must have been some massive Johnny Carson fan among the CIA contractors a that time!2011 Wayback Machine archive of iranfootballsource.com
. The third Iranian football on top of the two other published by Reuters: iraniangoalkicks.com and iraniangoals.com! Admittedly, this one is the most generic and less well designed one. But still. They pushed the theme too far!
The goalkeeper can be seen at: www.pixtastock.com/illustration/7323632.
2010 Wayback Machine archive of dedrickonline.com
. The German one.
The CIA has had a few Germany espionage scandals in the 2010s:
- 2014 www.bbc.co.uk/news/world-europe-28243933: a German Intelligence Agency agent was arrested for spying for the CIA
- 2021 www.reuters.com/world/europe/us-security-agency-spied-merkel-other-top-european-officials-through-danish-2021-05-30/ U.S. spied on Merkel and other Europeans through Danish cables
- 2020 www.dw.com/en/how-the-uss-cia-and-germanys-bnd-spied-on-world-leaders/a-52358527 it was revealed that Germany and the USA had an agreement to spy on world leaders, notably via compromised Swiss company Crypto AG
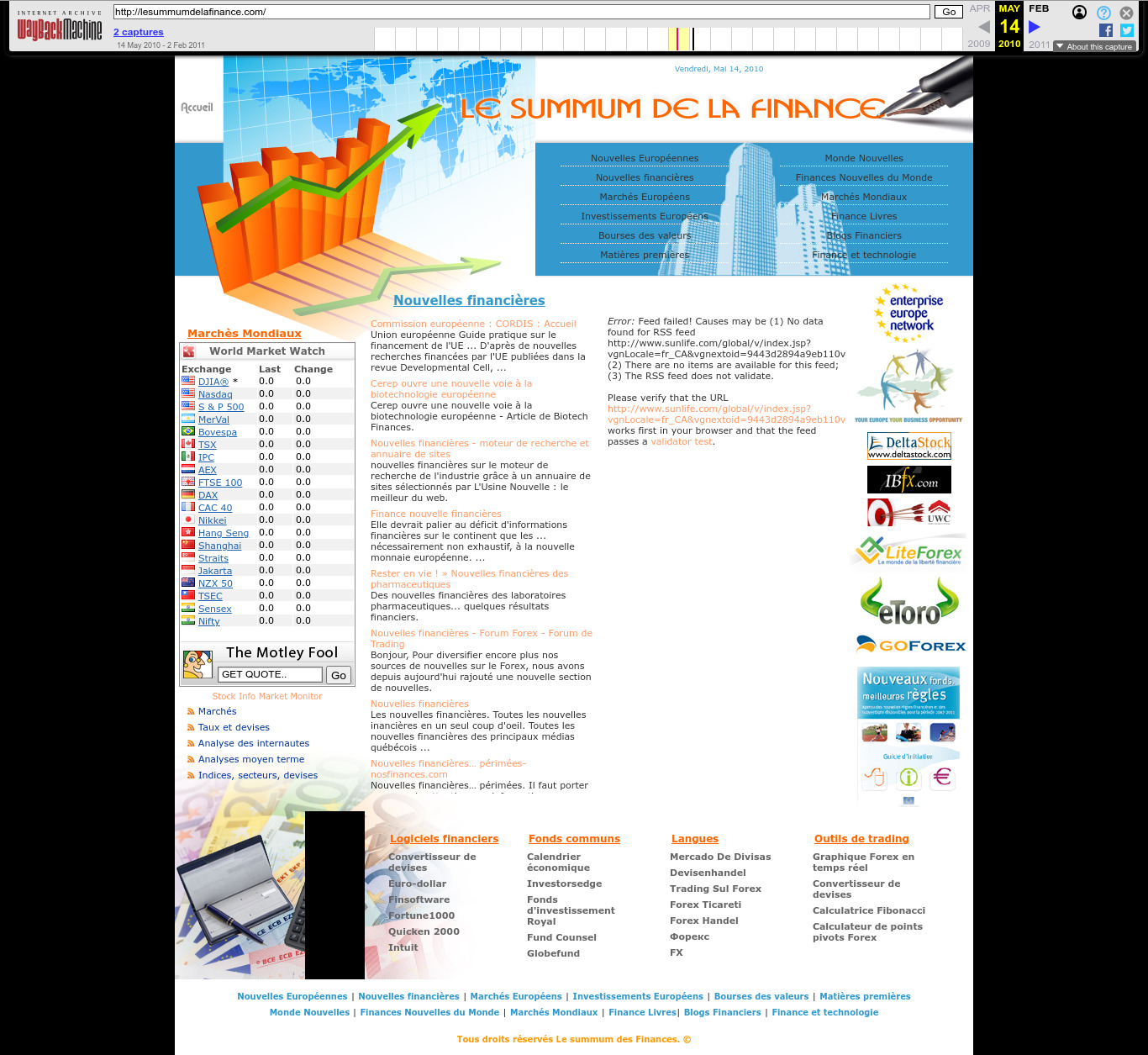
2010 Wayback Machine archive of lesummumdelafinance.com
. The arrow graph is very popular can be seen at: www.financialexpress.com/money/top-4-global-market-risks-for-2024-that-may-impact-your-finances-3346284/ and many other sites. Source unknown.
2011 Wayback Machine archive of economicnewsbuzz.com
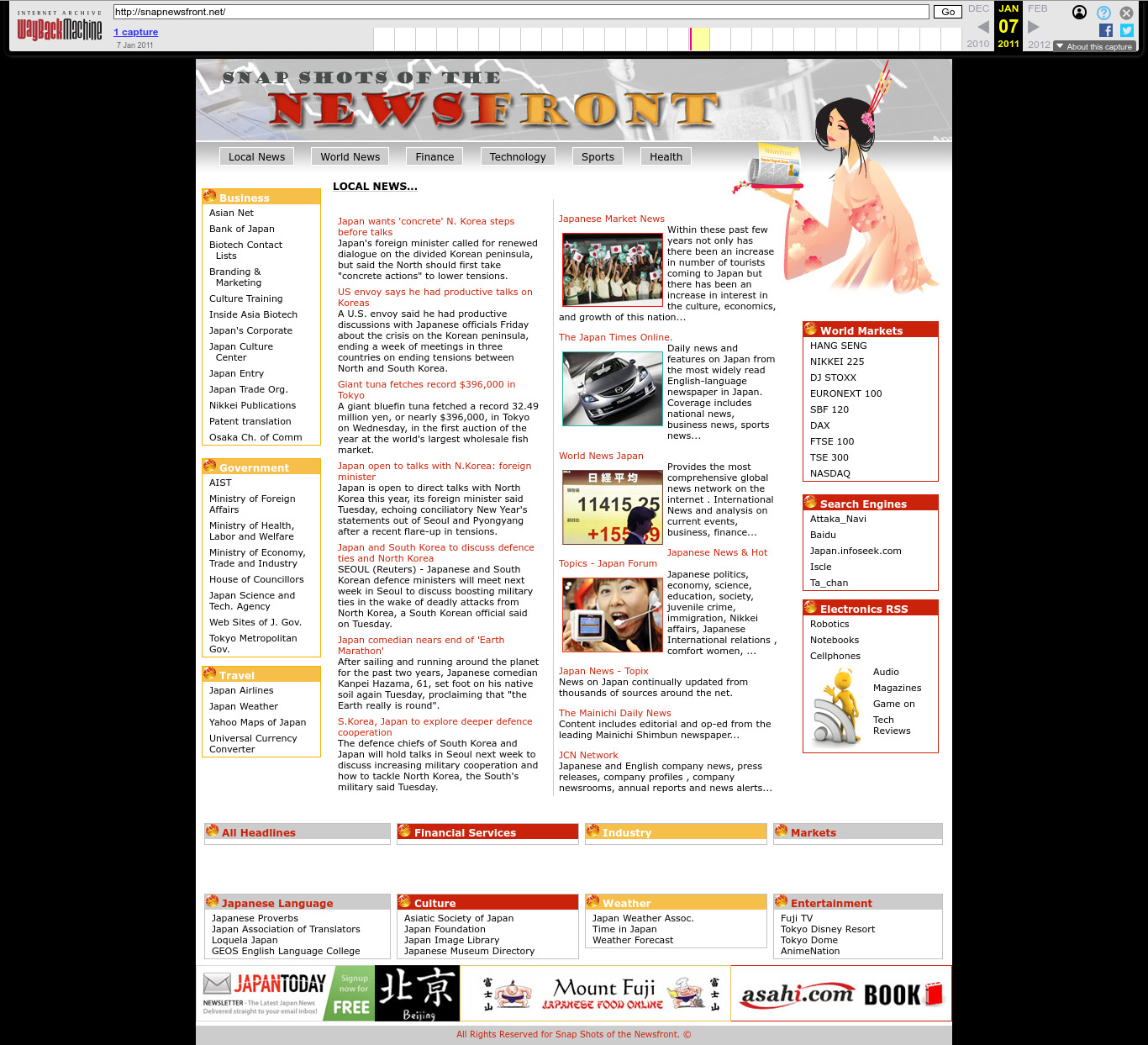
. The Korean one. Love the kawaii style!2011 Wayback Machine archive of snapnewsfront.net
. The Japanese one.
The geisha can be seen at: www.shutterstock.com/image-vector/pretty-geisha-16813348 by Larisa Frelke, assumed accounts: x.com/larra_vit | www.xing.com/profile/Larisa_Frelke
2010 Wayback Machine archive of philippinenewsonline.net
. The Philippine one one.2011 Wayback Machine archive of feedsdemexicoyelmundo.com
. The Mexican one.2012 Wayback Machine archive of easytraveleurope.com
. 2011 Wayback Machine archive of tee-shot.net
. One of the many golf-themed sites. Golf appears to be quite popular over in Langley. It's exactly what you'd expect for a mid-level spook to do in their free time!2011 Wayback Machine archive of nouvellesetdesrapports.com
. 2011 Wayback Machine archive of pangawana.com
. 2011 Wayback Machine archive of recuerdosdeviajeonline.com
. 2011 Wayback Machine archive of theworld-news.net
. 2011 Wayback Machine archive of kessingerssportsnews.com
. 2011 Wayback Machine archive of negativeaperture.com
. Pinned article: Introduction to the OurBigBook Project
Welcome to the OurBigBook Project! Our goal is to create the perfect publishing platform for STEM subjects, and get university-level students to write the best free STEM tutorials ever.
Everyone is welcome to create an account and play with the site: ourbigbook.com/go/register. We belive that students themselves can write amazing tutorials, but teachers are welcome too. You can write about anything you want, it doesn't have to be STEM or even educational. Silly test content is very welcome and you won't be penalized in any way. Just keep it legal!
Intro to OurBigBook
. Source. We have two killer features:
- topics: topics group articles by different users with the same title, e.g. here is the topic for the "Fundamental Theorem of Calculus" ourbigbook.com/go/topic/fundamental-theorem-of-calculusArticles of different users are sorted by upvote within each article page. This feature is a bit like:
- a Wikipedia where each user can have their own version of each article
- a Q&A website like Stack Overflow, where multiple people can give their views on a given topic, and the best ones are sorted by upvote. Except you don't need to wait for someone to ask first, and any topic goes, no matter how narrow or broad
This feature makes it possible for readers to find better explanations of any topic created by other writers. And it allows writers to create an explanation in a place that readers might actually find it.Figure 1. Screenshot of the "Derivative" topic page. View it live at: ourbigbook.com/go/topic/derivativeVideo 2. OurBigBook Web topics demo. Source. - local editing: you can store all your personal knowledge base content locally in a plaintext markup format that can be edited locally and published either:This way you can be sure that even if OurBigBook.com were to go down one day (which we have no plans to do as it is quite cheap to host!), your content will still be perfectly readable as a static site.
- to OurBigBook.com to get awesome multi-user features like topics and likes
- as HTML files to a static website, which you can host yourself for free on many external providers like GitHub Pages, and remain in full control
Figure 3. Visual Studio Code extension installation.Figure 4. Visual Studio Code extension tree navigation.Figure 5. Web editor. You can also edit articles on the Web editor without installing anything locally.Video 3. Edit locally and publish demo. Source. This shows editing OurBigBook Markup and publishing it using the Visual Studio Code extension.Video 4. OurBigBook Visual Studio Code extension editing and navigation demo. Source. - Infinitely deep tables of contents:
All our software is open source and hosted at: github.com/ourbigbook/ourbigbook
Further documentation can be found at: docs.ourbigbook.com
Feel free to reach our to us for any help or suggestions: docs.ourbigbook.com/#contact