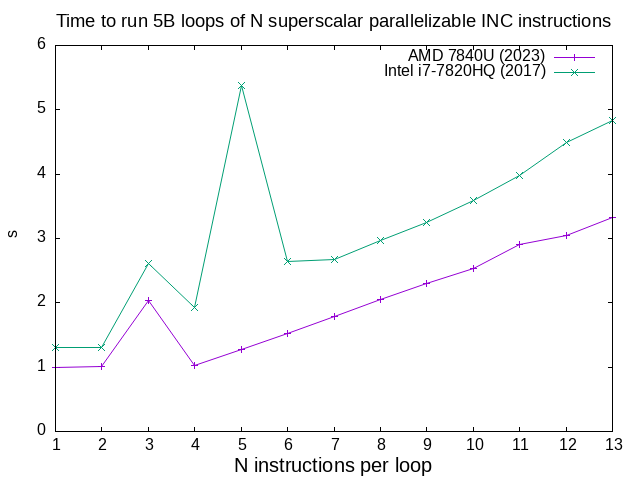
This is a quick Microarchitectural benchmark to try and determine how many functional units our CPU has that can do an
inc instruction at the same time due to superscalar architecture.The generated programs do loops like:with different numbers of inc instructions.
loop:
inc %[i0];
inc %[i1];
inc %[i2];
...
inc %[i_n];
cmp %[max], %[i0];
jb loop;c/inc_loop_asm_n.sh results for a few CPUs
. Quite clearly:and both have low instruction count effects that destroy performance, AMD at 3 and Intel at 3 and 5. TODO it would be cool to understand those better.
- AMD 7840U can run INC on 4 functional units
- Intel i7-7820HQ can run INC on 2 functional units
Data from multiple CPUs manually collated and plotted manually with ../c/inc_loop_asm_n_manual.sh.
Ubuntu 25.04 GCC 14.2 -O0 x86_64 produces a horrendous:To do about 1s on P14s we need 2.5 billion instructions:and:gives:
11c8: 48 83 45 f0 01 addq $0x1,-0x10(%rbp)
11cd: 48 8b 45 f0 mov -0x10(%rbp),%rax
11d1: 48 3b 45 e8 cmp -0x18(%rbp),%rax
11d5: 72 f1 jb 11c8 <main+0x7f>time ./inc_loop.out 2500000000time ./inc_loop.out 2500000000 1,052.22 msec task-clock # 0.998 CPUs utilized
23 context-switches # 21.858 /sec
12 cpu-migrations # 11.404 /sec
60 page-faults # 57.022 /sec
10,015,198,766 instructions # 2.08 insn per cycle
# 0.00 stalled cycles per insn
4,803,504,602 cycles # 4.565 GHz
20,705,659 stalled-cycles-frontend # 0.43% frontend cycles idle
2,503,079,267 branches # 2.379 G/sec
396,228 branch-misses # 0.02% of all branchesWith -O3 it manages to fully unroll the loop removing it entirely and producing:to is it smart enough to just return the return value from strtoll directly as is in
1078: e8 d3 ff ff ff call 1050 <strtoll@plt>
}
107d: 5a pop %rdx
107e: c3 retrax. The Amino-acid Sequence in the Phenylalanyl Chain of Insulin by  Ciro Santilli 40 Created 2025-06-17 Updated 2025-07-16
Ciro Santilli 40 Created 2025-06-17 Updated 2025-07-16
This is where he started publishing the sequence of insulin. The paper gives the full B-chain sequence, which it tentatively calls the "Phenylalanyl Chain" because it starts with a Phenylalanyl.
The official link seems to be: portlandpress.com/biochemj/article/49/4/463/47212/The-amino-acid-sequence-in-the-phenylalanyl-chain It seems to explain the methods very well at first glance, with lots of schematics.
This is one of those things that when astronomers first saw them they went "oh fuck we've found extraterrestrial life".
Some examples:
As described at Section "Radio astronomy", this new type of telescope led to the exciting discovery of new types of astronomical objects, notably pulsars and quasars.
Unlisted articles are being shown, click here to show only listed articles.