Lines through origin model of the real projective plane Updated 2025-07-16
This is the standard model.
List of AI games Updated 2025-07-16
List of anatomical systems Updated 2025-07-16
List of nuclear weapons Updated 2025-07-16
List of Stack Overflow users Updated 2025-09-09
List of version control systems Updated 2025-07-16
LLVM IR hello world Updated 2025-07-16
Example: llvm/hello.ll adapted from: llvm.org/docs/LangRef.html#module-structure but without double newline.
To execute it as mentioned at github.com/dfellis/llvm-hello-world we can either use their crazy assembly interpreter, tested on Ubuntu 22.10:This seems to use
sudo apt install llvm-runtime
lli hello.llputs from the C standard library.Or we can Lower it to assembly of the local machine:which produces:and then we can assemble link and run with gcc:or with clang:
sudo apt install llvm
llc hello.llhello.sgcc -o hello.out hello.s -no-pie
./hello.outclang -o hello.out hello.s -no-pie
./hello.outhello.s uses the GNU GAS format, which clang is highly compatible with, so both should work in general. LLVM IR vs C Updated 2025-07-16
Second quantization Updated 2025-07-16
Second quantization also appears to be useful not only for relativistic quantum mechanics, but also for condensed matter physics. The reason is that the basis idea is to use the number occupation basis. This basis is:
- convenient for quantum field theory because of particle creation and annihilation changes the number of particles all the time
- convenient for condensed matter physics because there you have a gazillion particles occupying entire energy bands
Bibliography:
- www.youtube.com/watch?v=MVqOfEYzwFY "How to Visualize Quantum Field Theory" by ZAP Physics (2020). Has 1D simulations on a circle. Starts towards the right direction, but is a bit lacking unfortunately, could go deeper.
Secrets (Allan Holdsworth album) Updated 2025-07-16
List of books Updated 2025-11-05
Local symmetries of the Lagrangian imply conserved currents Updated 2025-07-16
More precisely, each generator of the corresponding Lie algebra leads to one separate conserved current, such that a single symmetry can lead to multiple conserved currents.
This is basically the local symmetry version of Noether's theorem.
Then to maintain charge conservation, we have to maintain local symmetry, which in turn means we have to add a gauge field as shown at Video "Deriving the qED Lagrangian by Dietterich Labs (2018)".
Bibliography:
- photonics101.com/relativistic-electrodynamics/gauge-invariance-action-charge-conservation#show-solution has a good explanation of the Gauge transformation. TODO how does that relate to symmetry?
- physics.stackexchange.com/questions/57901/noether-theorem-gauge-symmetry-and-conservation-of-charge
London Updated 2025-07-16
Yung Professional Move to London by Sans Beanstalk
. Source. The sad thing is that the same author also has another accurate video criticizing British suburbia, so there's no escape basically in the UK: www.youtube.com/watch?v=oIJuZbXLZeY.
Video "Being a Dickhead's Cool by Reuben Dangoor (2010)" also comes to mind.
Loop (topology) Updated 2025-07-16
Lord of the Rings character Updated 2025-07-16
Lorentz covariance Updated 2025-07-16
Same motivation as Galilean invariance, but relativistic version of that: we want the laws of physics to have the same form on all inertial frames, so we really want to write them in a way that is Lorentz covariant.
This is just the relativistic version of that which takes the Lorentz transformation into account instead of just the old Galilean transformation.
Lorentz gauge condition Updated 2025-07-16
E.g. thinking about the electric potential alone, you could set the zero anywhere, and everything would remain be the same.
The Lorentz gauge is just one such choice. It is however a very popular one, because it is also manifestly Lorentz invariant.
Poincaré group Updated 2025-07-16
Full set of all possible special relativity symmetries:
In simple and concrete terms. Suppose you observe N particles following different trajectories in Spacetime.
There are two observers traveling at constant speed relative to each other, and so they see different trajectories for those particles:Note that the first two types of transformation are exactly the non-relativistic Galilean transformations.
- space and time shifts, because their space origin and time origin (time they consider 0, i.e. when they started their timers) are not synchronized. This can be modelled with a 4-vector addition.
- their space axes are rotated relative to one another. This can be modelled with a 4x4 matrix multiplication.
- and they are moving relative to each other, which leads to the usual spacetime interactions of special relativity. Also modelled with a 4x4 matrix multiplication.
The Poincare group is the set of all matrices such that such a relationship like this exists between two frames of reference.
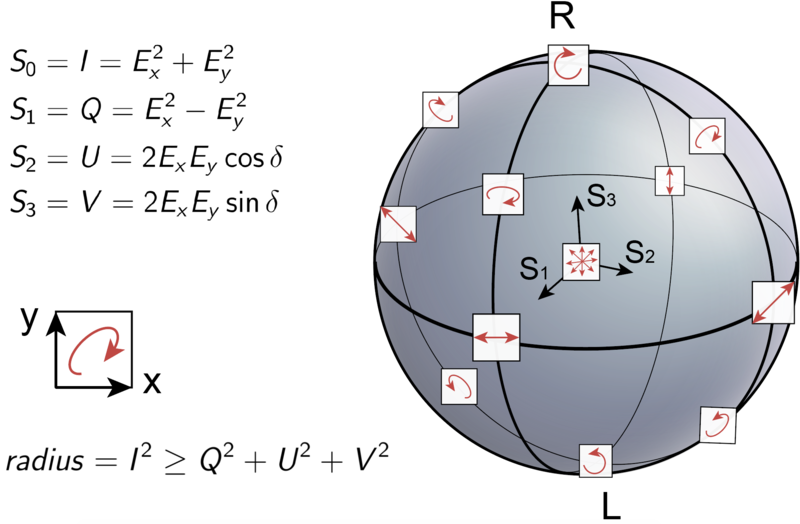
Poincaré sphere Updated 2025-07-16
In it, each of the six sides has a clear and simple to understand photon polarization state, either of:
The sphere clearly suggests for example that a rotational or diagonal polarizations are the combination of left/right with the correct phase. This is clearly explained at: Video "Quantum Mechanics 9b - Photon Spin and Schrodinger's Cat II by ViaScience (2013)".
Politics of Europe Updated 2025-07-16
Unlisted articles are being shown, click here to show only listed articles.