Ciro Santilli @cirosantilli 34

 Incoming links: Qubit

Alice&Bob  Updated 2024-12-15  +Created 1970-01-01

 View more

Funding rounds:

March 2022: 27M Euros

About their qubit:

alice-bob.com/2023/02/15/computing-256-bit-elliptic-curve-logarithm-in-9-hours-with-126133-cat-qubits/ Computing 256-bit elliptic curve logarithm in 9 hours with 126,133 cat qubits (2023). This describes their "cat qubit".

 Read the full article

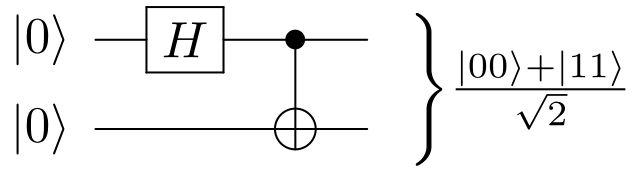
Bell circuit  Updated 2024-12-15  +Created 1970-01-01

 View more

A quantum circuit which when fed with input

∣ 00 ⟩

produces the Bell state.

In Qiskit at: qiskit/hello.py.

Figure 1.
Quantum circuit that generates the Bell state
. Source.
The fundamental intuition for this circuit is as follows.
First the Hadamard gate makes the first qubit be in a 50/50 state.
Then, the CNOT gate gets controlled by that 50/50 value, and the controlled qubit also gets 50/50 chance as a result.
However, both qubits are now entangled: the result of the second qubit depends on the result of the first one. Because:
if the first qubit is 0, cnot is not active, and so the second qubit remains 0 as its input
if the first qubit is 1, cnot is active, and so the second qubit is flipped to 1

 Read the full article

CNOT gate  Updated 2024-12-15  +Created 1970-01-01

 View more

The CNOT gate is a controlled quantum gate that operates on two qubits, flipping the second (operand) qubit if the first (control) qubit is set.

This gate is the first example of a controlled quantum gate that you should study.

⎣ ⎢ ⎢ ⎢ ⎡ 1000010000010010 ⎦ ⎥ ⎥ ⎥ ⎤

(1)

Equation 1.

CNOT gate matrix

Figure 1.
CNOT gate symbol
. Source. The symbol follow the generic symbol convention for controlled quantum gates shown at Figure "Generic controlled quantum gate symbol", but replacing the generic "U" with the Figure "Quantum NOT gate symbol".

To understand why the gate is called a CNOT gate, you should think as follows.

First let's produce a generic quantum state vector where the control qubit is certain to be 0.

On the standard basis:

∣ 00 ⟩ ∣ 01 ⟩ ∣ 10 ⟩ ∣ 11 ⟩

(2)

we see that this means that only

∣ 00 ⟩

and

∣ 01 ⟩

should be possible. Therefore, the state must be of the form:

⎣ ⎢ ⎢ ⎢ ⎡ x y 00 ⎦ ⎥ ⎥ ⎥ ⎤

(3)

where

x

and

y

are two complex numbers such that

∣ x ∣ + ∣ y ∣ = 1.0

If we operate the CNOT gate on that state, we obtain:

⎣ ⎢ ⎢ ⎢ ⎡ 1000010000010010 ⎦ ⎥ ⎥ ⎥ ⎤ \times ⎣ ⎢ ⎢ ⎢ ⎡ x y 00 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ x y 00 ⎦ ⎥ ⎥ ⎥ ⎤

(4)

and so the input is unchanged as desired, because the control qubit is 0.

If however we take only states where the control qubit is for sure 1:

⎣ ⎢ ⎢ ⎢ ⎡ 1000010000010010 ⎦ ⎥ ⎥ ⎥ ⎤ \times ⎣ ⎢ ⎢ ⎢ ⎡ 00 x y ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ 00 y x ⎦ ⎥ ⎥ ⎥ ⎤

(5)

Therefore, in that case, what happened is that the probabilities of

∣ 10 ⟩

and

∣ 11 ⟩

were swapped from

x

and

y

y

and

x

respectively, which is exactly what the quantum NOT gate does.

So from this we understand more concretely what "the gate only operates if the first qubit is set to one" means.

Now go and study the Bell state and understand intuitively how this gate is used to produce it.

 Read the full article

Continuous-variable quantum information  Updated 2024-12-15  +Created 1970-01-01

 View more

TODO synonym to analog quantum computer?

It is also possible to carry out quantum computing without qubits using processes with a continuous spectrum of measurement.

As of 2020, these approaches seem less developed/promising, but who knows.

These computers can be seen as analogous to classical non-quantum analog computers.

 Read the full article

Controlled quantum gate  Updated 2024-12-15  +Created 1970-01-01

 View more

Controlled quantum gates are gates that have two types of input qubits:

control qubits
operand qubits (terminology made up by Ciro Santilli just now)

These gates can be understood as doing a certain unitary operation only if the control qubits are enabled or disabled.

The first example to look at is the CNOT gate.

Figure 1.
Generic controlled quantum gate symbol
. Source.
The black dot means "control qubit", and "U" means an arbitrary Unitary operation.
When the operand has a conventional symbol, e.g. the Figure "Quantum NOT gate symbol" for the quantum NOT gate to form the CNOT gate, that symbol is used in the operand instead.

 Read the full article

@cirosantilli/_file/qiskit/qiskit/hello.py  Updated 2024-12-15  +Created 1970-01-01

 View more

Our example uses a Bell state circuit to illustrate all the fundamental Qiskit basics.

Sample program output, counts are randomized each time.

First we take the quantum state vector immediately after the

∣ 00 ⟩

input.

input:
state:
Statevector([1.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
            dims=(2, 2))
probs:
[1. 0. 0. 0.]

We understand that the first element of Statevector is

∣ 00 ⟩

, and has probability of 1.0.

Next we take the state after a Hadamard gate on the first qubit:

h:
state:
Statevector([0.70710678+0.j, 0.70710678+0.j, 0.        +0.j,
             0.        +0.j],
            dims=(2, 2))
probs:
[0.5 0.5 0.  0. ]

We now understand that the second element of the Statevector is

∣ 01 ⟩

, and now we have a 50/50 propabability split for the first bit.

Then we apply the CNOT gate:

cx:
state:
Statevector([0.70710678+0.j, 0.        +0.j, 0.        +0.j,
             0.70710678+0.j],
            dims=(2, 2))
probs:
[0.5 0.  0.  0.5]

which leaves us with the final

\frac{∣ 0 0 ⟩ + ∣ 1 1 ⟩}{2}

Then we print the circuit a bit:

qc without measure:
     ┌───┐
q_0: ┤ H ├──■──
     └───┘┌─┴─┐
q_1: ─────┤ X ├
          └───┘
c: 2/══════════

qc with measure:
     ┌───┐     ┌─┐
q_0: ┤ H ├──■──┤M├───
     └───┘┌─┴─┐└╥┘┌─┐
q_1: ─────┤ X ├─╫─┤M├
          └───┘ ║ └╥┘
c: 2/═══════════╩══╩═
                0  1
qasm:
OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
h q[0];
cx q[0],q[1];
measure q[0] -> c[0];
measure q[1] -> c[1];

And finally we compile the circuit and do some sample measurements:

qct:
     ┌───┐     ┌─┐
q_0: ┤ H ├──■──┤M├───
     └───┘┌─┴─┐└╥┘┌─┐
q_1: ─────┤ X ├─╫─┤M├
          └───┘ ║ └╥┘
c: 2/═══════════╩══╩═
                0  1
counts={'11': 484, '00': 516}
counts={'11': 493, '00': 507}

 Read the full article

Measurement-based quantum computer  Updated 2024-12-15  +Created 1970-01-01

 View more

TODO confirm: apparently in the paradigm you can choose to measure only certain output qubits.

This makes things irreversible (TODO what does reversibility mean in this random context?), as opposed to Circuit-based quantum computer where you measure all output qubits at once.

TODO what is the advantage?

 Read the full article

Phasecraft  Updated 2024-12-15  +Created 1970-01-01

 View more

www.phasecraft.io

The co-founder's name, Toby Cubitt, is the mos awesome thing ever (Cubitt -> qubit). From UCL.

Funding:

2023: £13m: www.uktech.news/deep-tech/phasecraft-quantum-computing-20230816

 Read the full article

Programmer's model of quantum computers  Updated 2024-12-15  +Created 1970-01-01

 View more

This is a quick tutorial on how a quantum computer programmer thinks about how a quantum computer works. If you know:

what a complex number is
how to do matrix multiplication
what is a probability

a concrete and precise hello world operation can be understood in 30 minutes.

Although there are several types of quantum computer under development, there exists a single high level model that represents what most of those computers can do, and we are going to explain that model here. This model is the is the digital quantum computer model, which uses a quantum circuit, that is made up of many quantum gates.

Beyond that basic model, programmers only may have to consider the imperfections of their hardware, but the starting point will almost always be this basic model, and tooling that automates mapping the high level model to real hardware considering those imperfections (i.e. quantum compilers) is already getting better and better.

This model is very simple to understand, being only marginally more complex than that of a classical computer, see also: quantumcomputing.stackexchange.com/questions/6639/is-my-background-sufficient-to-start-quantum-computing/14317#14317

The situation of quantum computers today in the 2020's is somewhat analogous to that of the early days of classical circuits and computers in the 1950's and 1960's, before CPU came along and software ate the world. Even though the exact physics of a classical computer might be hard to understand and vary across different types of integrated circuits, those early hardware pioneers (and to this day modern CPU designers), can usefully view circuits from a higher level point of view, thinking only about concepts such as:

logic gates like AND, NOR and NOT
a clock + registers

as modelled at the register transfer level, and only in a separate compilation step translated into actual chips. This high level understanding of how a classical computer works is what we can call "the programmer's model of a classical computer". So we are now going to describe the quantum analogue of it.

The way quantum programmers think about a quantum computer in order to program can be described as follows:

the input of a N qubit quantum computer is a vector of dimension N containing classic bits 0 and 1
the quantum program, also known as circuit, is a $2^{n} \times 2^{n}$ unitary matrix of complex numbers $Q \in C^{2^{n}} \times C^{2^{n}}$ that operates on the input to generate the output
the output of a N qubit computer is also a vector of dimension N containing classic bits 0 and 1

To operate a quantum computer, you follow the step of operation of a quantum computer:

set the input qubits to classic input bits (state initialization)
press a big red "RUN" button
read the classic output bits (readout)

Each time you do this, you are literally conducting a physical experiment of the specific physical implementation of the computer:

setup your physical system to represent the classical 0/1 inputs
let the state evolve for long enough
measure the classical output back out

and each run as the above can is simply called "an experiment" or "a measurement".

The output comes out "instantly" in the sense that it is physically impossible to observe any intermediate state of the system, i.e. there are no clocks like in classical computers, further discussion at: quantum circuits vs classical circuits. Setting up, running the experiment and taking the does take some time however, and this is important because you have to run the same experiment multiple times because results are probabilistic as mentioned below.

Unlike in a classical computer, the output of a quantum computer is not deterministic however.

But the each output is not equally likely either, otherwise the computer would be useless except as random number generator!

This is because the probabilities of each output for a given input depends on the program (unitary matrix) it went through.

Therefore, what we have to do is to design the quantum circuit in a way that the right or better answers will come out more likely than the bad answers.

We then calculate the error bound for our circuit based on its design, and then determine how many times we have to run the experiment to reach the desired accuracy.

The probability of each output of a quantum computer is derived from the input and the circuit as follows.

First we take the classic input vector of dimension N of 0's and 1's and convert it to a "quantum state vector"

q_{i n}

of dimension

2^{n}

q_{i n} \in C^{2^{n}}

(1)

We are after all going to multiply it by the program matrix, as you would expect, and that has dimension

2^{n} \times 2^{n}

Note that this initial transformation also transforms the discrete zeroes and ones into complex numbers.

For example, in a 3 qubit computer, the quantum state vector has dimension

2^{3} = 8

and the following shows all 8 possible conversions from the classic input to the quantum state vector:

000 -> 1000 0000 == (1.0, 0.0, 0.0, 0.0,  0.0, 0.0, 0.0, 0.0)
001 -> 0100 0000 == (0.0, 1.0, 0.0, 0.0,  0.0, 0.0, 0.0, 0.0)
010 -> 0010 0000 == (0.0, 0.0, 1.0, 0.0,  0.0, 0.0, 0.0, 0.0)
011 -> 0001 0000 == (0.0, 0.0, 0.0, 1.0,  0.0, 0.0, 0.0, 0.0)
100 -> 0000 1000 == (0.0, 0.0, 0.0, 0.0,  1.0, 0.0, 0.0, 0.0)
101 -> 0000 0100 == (0.0, 0.0, 0.0, 0.0,  0.0, 1.0, 0.0, 0.0)
110 -> 0000 0010 == (0.0, 0.0, 0.0, 0.0,  0.0, 0.0, 1.0, 0.0)
111 -> 0000 0001 == (0.0, 0.0, 0.0, 0.0,  0.0, 0.0, 0.0, 1.0)

This can be intuitively interpreted as:

if the classic input is 000, then we are certain that all three bits are 0.
Therefore, the probability of all three 0's is 1.0, and all other possible combinations have 0 probability.
if the classic input is 001, then we are certain that bit one and two are 0, and bit three is 1. The probability of that is 1.0, and all others are zero.
and so on

Now that we finally have our quantum state vector, we just multiply it by the unitary matrix

Q

of the quantum circuit, and obtain the

2^{n}

dimensional output quantum state vector

q_{o u t}

q_{o u t} = Q q_{i n}

(2)

And at long last, the probability of each classical outcome of the measurement is proportional to the square of the length of each entry in the quantum vector, analogously to what is done in the Schrödinger equation.

For example, suppose that the 3 qubit output were:

q_{o u t} = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \frac{3}{2} 0.0 \frac{1}{2} 0.0 0.0 0.0 0.0 0.0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤

(3)

Then, the probability of each possible outcomes would be the length of each component squared:

P (000) P (001) P (010) P (011) P (100) P (101) P (110) P (111) = ∣ ∣ ∣ ∣ ∣ ∣ \frac{3}{2} ∣ ∣ ∣ ∣ ∣ ∣^{2} = ∣ 0 ∣^{2} = ∣ ∣ ∣ ∣ ∣ ∣ \frac{1}{2} ∣ ∣ ∣ ∣ ∣ ∣^{2} = ∣ 0 ∣^{2} = ∣ 0 ∣^{2} = ∣ 0 ∣^{2} = ∣ 0 ∣^{2} = ∣ 0 ∣^{2} = \frac{3}{2}^{2} = 0^{2} = \frac{1}{2}^{2} = 0^{2} = 0^{2} = 0^{2} = 0^{2} = 0^{2} = \frac{3}{4} = 0 = \frac{1}{4} = 0 = 0 = 0 = 0 = 0

(4)

i.e. 75% for the first, and 25% for the third outcomes, where just like for the input:

first outcome means 000: all output bits are zero
third outcome means 010: the first and third bits are zero, but the second one is 1

All other outcomes have probability 0 and cannot occur, e.g.: 001 is impossible.

Keep in mind that the quantum state vector can also contain complex numbers because we are doing quantum mechanics, but we just take their magnitude in that case, e.g. the following quantum state would lead to the same probabilities as the previous one:

∣ ∣ ∣ ∣ ∣ ∣ \frac{1 + 2 i}{2} ∣ ∣ ∣ ∣ ∣ ∣^{2} ∣ ∣ ∣ ∣ ∣ \frac{i}{2} ∣ ∣ ∣ ∣ ∣^{2} = \frac{1 ^{2} + 2 ^{2}}{2 ^{2}} = \frac{1 ^{2}}{2 ^{2}} = \frac{3}{4} = \frac{1}{4}

(5)

This interpretation of the quantum state vector clarifies a few things:

the input quantum state is just a simple state where we are certain of the value of each classic input bit
the matrix has to be unitary because the total probability of all possible outcomes must be 1.0
This is true for the input matrix, and unitary matrices have the probability of maintaining that property after multiplication.
Unitary matrices are a bit analogous to self-adjoint operators in general quantum mechanics (self-adjoint in finite dimensions implies is stronger)
This also allows us to understand intuitively why quantum computers may be capable of accelerating certain algorithms exponentially: that is because the quantum computer is able to quickly do an unitary matrix multiplication of a humongous $2^{N}$ sized matrix.
If we are able to encode our algorithm in that matrix multiplication, considering the probabilistic interpretation of the output, then we stand a chance of getting that speedup.

Bibliography:

arxiv.org/pdf/1804.03719.pdf Quantum Algorithm Implementations for Beginners by Abhijith et al. 2020

 Read the full article

qiskit/initialize.py  Updated 2024-12-15  +Created 1970-01-01

 View more

In this example we will initialize a quantum circuit with a single CNOT gate and see the output values.

By default, Qiskit initializes every qubit to 0 as shown in the qiskit/hello.py. But we can also initialize to arbitrary values as would be done when computing the output for various different inputs.

Output:

     ┌──────────────────────┐
q_0: ┤0                     ├──■──
     │  Initialize(1,0,0,0) │┌─┴─┐
q_1: ┤1                     ├┤ X ├
     └──────────────────────┘└───┘
c: 2/═════════════════════════════

init: [1, 0, 0, 0]
probs: [1. 0. 0. 0.]

init: [0, 1, 0, 0]
probs: [0. 0. 0. 1.]

init: [0, 0, 1, 0]
probs: [0. 0. 1. 0.]

init: [0, 0, 0, 1]
probs: [0. 1. 0. 0.]

     ┌──────────────────────────────────┐
q_0: ┤0                                 ├──■──
     │  Initialize(0.70711,0,0,0.70711) │┌─┴─┐
q_1: ┤1                                 ├┤ X ├
     └──────────────────────────────────┘└───┘
c: 2/═════════════════════════════════════════

init: [0.7071067811865475, 0, 0, 0.7071067811865475]
probs: [0.5 0.5 0.  0. ]

which we should all be able to understand intuitively given our understanding of the CNOT gate and quantum state vectors.

quantumcomputing.stackexchange.com/questions/13202/qiskit-initializing-n-qubits-with-binary-values-0s-and-1s describes how to initialize circuits qubits only with binary 0 or 1 to avoid dealing with the exponential number of elements of the quantum state vector.

 Read the full article

Quantum algorithm vs quantum gate vs quantum circuit  Updated 2024-12-15  +Created 1970-01-01

 View more

There is no fundamental difference between them, a quantum algorithm is a quantum circuit, which can be seen as a super complicated quantum gate.

Perhaps the greats practical difference is that algorithms tend to be defined for an arbitrary number of N qubits, i.e. as a function for that each N produces a specific quantum circuit with N qubits solving the problem. Most named gates on the other hand have fixed small sizes.

 Read the full article

Superconducting qubits are bad because of fabrication variation  Updated 2024-12-15  +Created 1970-01-01

 View more

Atom-based qubits like trapped ion quantum computers have parameters fixed by the laws of physics.

However superconducting qubits have a limit on how precise their parameters can be set based on how well we can fabricate devices. This may require per-device characterisation.

 Read the full article

Tensor product in quantum computing  Updated 2024-12-15  +Created 1970-01-01

 View more

We don't need to understand a super generalized version of tensor products to know what they mean in basic quantum computing!

Intuitively, taking a tensor product of two qubits simply means putting them together on the same quantum system/computer.

When we write the bra-ket notation:

∣ 00 ⟩

that is the same as

∣ 0 ⟩ \otimes ∣ 0 ⟩

The tensor product is called a "product" because it distributes over addition.

E.g. consider:

(\frac{∣ 0 ⟩ + ∣ 1 ⟩}{2}) \otimes ∣ 0 ⟩ = \frac{∣ 0 ⟩ \otimes ∣ 0 ⟩ + ∣ 1 ⟩ \otimes ∣ 0 ⟩}{2} = \frac{∣ 0 0 ⟩ + ∣ 1 0 ⟩}{2}

(1)

Intuitively, in this operation we just put a Hadamard gate qubit together with a second pure

∣ 0 ⟩

qubit.

And the outcome still has the second qubit as always 0, because we haven't made them interact.

The quantum state

\frac{∣ 0 0 ⟩ + ∣ 1 0 ⟩}{2}

is called a separable state, because it can be written as a single product of two different qubits. We have simply brought two qubits together, without making them interact.

If we then add a CNOT gate to make a Bell state:

\frac{∣ 0 0 ⟩ + ∣ 1 1 ⟩}{2} = \frac{∣ 0 ⟩ \otimes ∣ 0 ⟩ + ∣ 1 ⟩ \otimes ∣ 1 ⟩}{2}

(2)

we can now see that the Bell state is non-separable: we've made the two qubits interact, and there is no way to write this state with a single tensor product. The qubits are fundamentally entangled.

 Read the full article