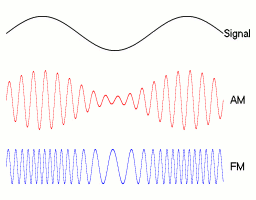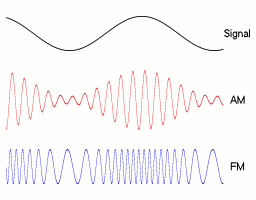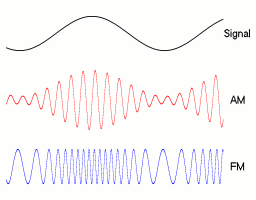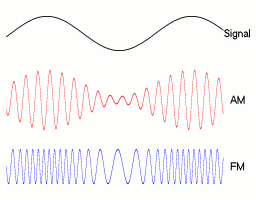
But now people want to send voice. How to do it?
It would not be practical without modulation: Why can't you send voice without modulation?
Introductory Quantum Mechanics by Richard Fitzpatrick (2020) by  Ciro Santilli 40 Updated 2025-07-16
Ciro Santilli 40 Updated 2025-07-16
This LibreTexts book does have some interest!
Last updated: 2013.
There were apparently some lecture videos at: web.archive.org/web/20030604194654/http://physicsstream.ucsd.edu/courses/spring2003/physics130a/ as pointed out by Matthew Heaney[ref], .mov files can be found at: web.archive.org/web/*/http://physicsstream.ucsd.edu/courses/spring2003/physics130a/*, but we were yet unable to open them, related:
This is the true key question: what are the most important algorithms that would be accelerated by quantum computing?
Some candidates:
- Shor's algorithm: this one will actually make humanity worse off, as we will be forced into post-quantum cryptography that will likely be less efficient than existing classical cryptography to implement
- quantum algorithm for linear systems of equations, and related application of systems of linear equations
- Grover's algorithm: speedup not exponential. Still useful for anything?
- Quantum Fourier transform: TODO is the speedup exponential or not?
- Deutsch: solves an useless problem
- NISQ algorithms
Maybe there is some room for doubt because some applications might be way better in some implementations, but we should at least have a good general idea.
However, clear information on this really hard to come by, not sure why.
Whenever asked e.g. at: physics.stackexchange.com/questions/3390/can-anybody-provide-a-simple-example-of-a-quantum-computer-algorithm/3407 on Physics Stack Exchange people say the infinite mantra:
Lists:
- Quantum Algorithm Zoo: the leading list as of 2020
- quantum computing computational chemistry algorithms is the area that Ciro and many people are te most excited about is
- cstheory.stackexchange.com/questions/3888/np-intermediate-problems-with-efficient-quantum-solutions
- mathoverflow.net/questions/33597/are-there-any-known-quantum-algorithms-that-clearly-fall-outside-a-few-narrow-cla
At Section "Quantum computing is just matrix multiplication" we saw that making a quantum circuit actually comes down to designing one big unitary matrix.
Instead, they use quantum logic gates.
One important area of research and development of quantum computing is the development of benchmarks that allow us to compare different quantum computers to decide which one is more powerful than the other.
Ideally, we would like to be able to have a single number that predicts which computer is more powerful than the other for a wide range of algorithms.
However, much like in CPU benchmarking, this is a very complex problem, since different algorithms might perform differently in different architectures, making it very hard to sum up the architecture's capabilities to a single number as we would like.
The only thing that is directly comparable across computers is how two machines perform for a single algorithm, but we want a single number that is representative of many algorithms.
For example, the number of qubits would be a simple naive choice of such performance predictor number. But it is very imprecise, since other factors are also very important:
Quantum volume is another less naive attempt at such metric.
This is one of the first examples in most quantum field theory.
It usually does not involve any forces, just the interpretation of what the quantum field is.
www.youtube.com/watch?v=zv94slY6WqY&list=PLSpklniGdSfSsk7BSZjONcfhRGKNa2uou&index=2 Quantization Of A Free Real Scalar Field by Dietterich Labs (2019)
Founder: Peter Armstrong
ruboss.com/ documents their stack, a somewhat similar choice to OurBigBook.com as of 2021, notably Next.js. But backend in Ruby on Rails. They actually managed Apollo/GraphQL, which Ciro Santilli would have liked, but din't have the patience for.
The founder/CEO Peter Armstrong www.linkedin.com/in/peterburtonarmstrong/ He looks like a nice guy.
The only isotope found on Earth because it occurs as part of the uranium 238 decay chain, i.e., it is not a primordial nuclide.
Ah, Ciro Santilli was not expecting this. What a unique mixture of humour, technology, politics and bravery. No wonder it was a box flop, there's something good about this film.
Unlisted articles are being shown, click here to show only listed articles.