Sample software implementations:
The name is a bit obscure if you don't think in very generalized terms right out of the gate. It refers to a linear polynomial of multiple variables, which by definition must have the super simple form of:and then we just put the unknown and each derivative into that simple polynomial:except that now the are not just constants, but they can also depend on the argument (but not on or its derivatives).
Explicit solutions exist for the very specific cases of:
- constant coefficients, any degree. These were known for a long time, and are were studied when Ciro was at university in the University of São Paulo.
- degree 1 and any coefficient
Order of the highest derivative that appears.
Technique to solve partial differential equations
Naturally leads to the Fourier series, see: solving partial differential equations with the Fourier series, and to other analogous expansions:
One notable application is the solution of the Schrödinger equation via the time-independent Schrödinger equation.
Bibliography:
The finite element method is one of the most common ways to solve PDEs in practice.
Used to solve partial differential equation.
TODO confirm: does the solution of the heat equation always converge to the solution of the Laplace equation as time tends to infinity?
In one dimension, the Laplace equation is boring as it is just a straight line since the second derivative must be 0. That also matches our intuition of the limit solution of the heat equation.
Show up when solving the Laplace's equation on spherical coordinates by separation of variables, which leads to the differential equation shown at: en.wikipedia.org/w/index.php?title=Legendre_polynomials&oldid=1018881414#Definition_via_differential_equation.
Generalization of Laplace's equation where the value is not necessarily 0.
A solution to Laplace's equation.
Correspond to the angular part of Laplace's equation in spherical coordinates after using separation of variables as shown at: en.wikipedia.org/wiki/Spherical_harmonics#Laplace's_spherical_harmonics
Besides being useful in engineering, it was very important historically from a "development of mathematics point of view", e.g. it was the initial motivation for the Fourier series.
Some interesting properties:
- TODO confirm: for a fixed boundary condition that does not depend on time, the solutions always approaches one specific equilibrium function.This is in contrast notably with the wave equation, which can oscillate forever.
- TODO: for a given point, can the temperature go down and then up, or is it always monotonic with time?
- information propagates instantly to infinitely far. Again in contrast to the wave equation, where information propagates at wave speed.
Sample numerical solutions:
See: math.stackexchange.com/questions/579453/real-world-application-of-fourier-series/3729366#3729366
As mentioned at: math.stackexchange.com/questions/579453/real-world-application-of-fourier-series/3729366#3729366 from solving partial differential equations with the Fourier series citing courses.maths.ox.ac.uk/node/view_material/1720, analogously to the heat equation, the wave linear equation can be be solved nicely with separation of variables.
Staring from a triangle wave, this explains why we always get the same musical notes:See also: solving partial differential equations with the Fourier series.
- www.math.hmc.edu/~ajb/PCMI/lecture7.pdf "7.5.1. Musical instruments" is very good. Also mentions that in the piano it is more like an initial speed is applied, and it is not the same as plucking
- music.stackexchange.com/questions/135635/confusion-about-overtones-and-a-slow-motion-video-of-a-plucked-string
- music.stackexchange.com/questions/60833/what-determines-the-relative-volumes-of-the-harmonics-when-plucking-a-guitar-str
This section talks about solvers/simulators dedicated solving the wave equation. Of course, any serious solver will likely be able to solve a wider range of PDE, so this section contains mostly fun toys. For more serious stuff see: Section "PDE solver".
JavaScript toy solvers:
- jtiscione.github.io/webassembly-wave/index.html circular domain, create waves with mouse click
- dionyziz.com/graphics/wave-experiment/ with useless 3D WebGL visualization :-), waves with mouse click. Solving itself done on CPU, not GPU.
web.archive.org/web/20200621205928/https://courses.maths.ox.ac.uk/node/view_material/1720 also mentioned at math.stackexchange.com/questions/579453/real-world-application-of-fourier-series/3729366#3729366 from heat equation solution with Fourier series.
TODO confirm, see also: coupled oscillators. And then this idea can be used to define/motivate quantum field theory in terms of quantum harmonic oscillators with second quantization.
- youtu.be/SMmFgIEGYtw?t=324 Quantum Field Theory 2a - Field Quantization I by ViaScience (2018)
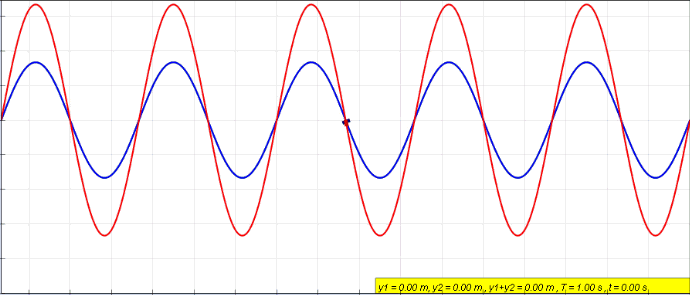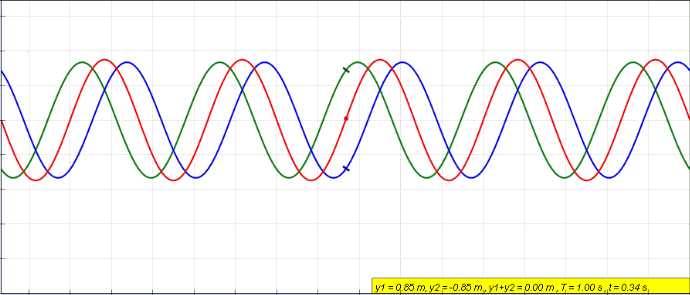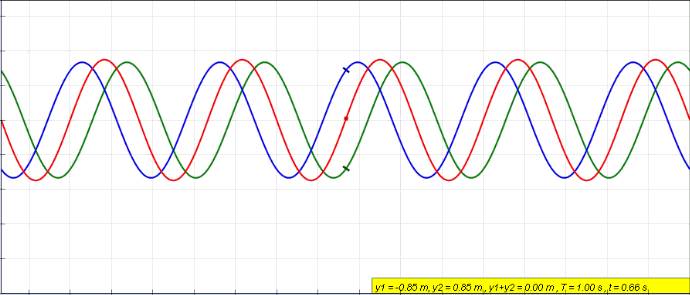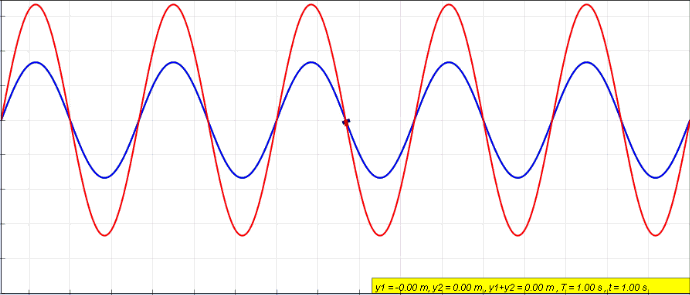
Standing wave caused by wave interference of two waves
. Source. Start with: Section "String polarization".
Then go to: Section "Polarization of light".
This is about the polarization of a string in 3D space. That is the first concept of polarization you must have in mind!
Far field approximation to Kirchhoff's diffraction formula, i.e. when the plane of observation is far from the object diffracting.
Near field approximation to Kirchhoff's diffraction formula, i.e. when the plane of observation is near the object diffracting.
Examples:
- mechanical resonance, notably:
- pipe instruments
- electronic oscillators, notably:
- LC oscillator, and notably the lossy version RLC circuit
Perhaps a key insight of resonance is that the reonant any lossy system tends to look like the resonance frequency quite quickly even if the initial condition is not the resonant condition itself, because everything that is not the resonant frequency interferes destructively and becomes noise. Some examples of that:
- striking a bell or drum can be modelled by applying an impuse to the system
- playing a pipe instrument comes down to blowing a piece that vibrates randomly, and then leads the pipe to vibrate mostly in the resonant frequency. Likely the same applies to bowed string instruments, the bow must be creating a random vibration.
- playing a plucked string instrument comes down to initializing the system to an triangular wave form and then letting it evolve. TODO find a simulation of that!
Another cool aspect of resonance is that it was kind of the motivation for de Broglie hypothesis, as de Broglie was kind of thinking that electroncs might show discrete jumps on atomic spectra because of constructive interference.
Notably used for the pattern of the double-slit experiment.
Shows up when trying to solve 2D wave equation on a circular domain in polar coordinates with separation of variables, where we have to decompose the initial condition in termes of a fourier-Bessel series, exactly like the Fourier series appears when solving the wave equation in linear coordinates.
For the same fundamental reasons, also appears when calculating the Schrödinger equation solution for the hydrogen atom.
Completeness: math.stackexchange.com/questions/2192665/is-this-set-of-bessel-functions-a-basis-for-all-c10-a-functions TODO
This is the Bessel function analogue to Fourier basis is complete for .
eigenvalue problem of Laplace's equation.
Unlike for ordinary differential equations which have the Picard–Lindelöf theorem, the existence and uniqueness of solution is not well solved for PDEs.
For example, Navier-Stokes existence and smoothness was one of the Millennium Prize Problems.
Started in 1987 and written in Pascal, by the French from Pierre and Marie Curie University, the French are really strong in numerical analysis.
The fact that French wrote it can be seen in the documentation, for example doc.freefem.org/tutorials/index.html uses file extension
mycode.edp instead of mycode.pde where dep stands for "Équation aux dérivées partielles".Besides the painful build, using FreeFem is relatively simple, as can be seen from the examples on the website.
They do use a domain-specific language on the examples, which appears to be the main/only interface, which is a bad thing, Ciro would rather have a Python API as the "main API", which is more the approach taken by the FEniCS Project, but so be it. This domain-specific language business means that you always stumble upon basic stuff you want to do but can't, and then you have to think about how to share data between the simulation and the plotting. The plotting notably is super complex and they can't implement all of what people want, upstream examples often offload that to gnuplot. This is potentially a big advantage of FEniCS Project.
It nice though that they do have some graphics out of the box, as that allows to quickly debug common problems.
Uses variational formulation of a partial differential equation, which is not immediately obvious to beginners? The introduction doc.freefem.org/tutorials/poisson.html gives an ultra quick example, but your are mostly on your own with that.
On Ubuntu 20.04, the
freefem is a bit out-of-date (3.5.8, there isn't even a tag for that in the GitHub repo, and refs/tags/release_3_10 is from 2010!) and fails to run the examples from the website. It did work with the example package though, but the output does not have color, which makes me sad :-)sudo apt install freefem freefem-examples
freefem /usr/share/doc/freefem-examples/heat.pdeSo let's just compile the latest v4.6 it from source, on Ubuntu 20.04:
sudo apt build-dep freefem
git clone https://github.com/FreeFem/FreeFem-sources
cd FreeFem-sources
# Post v4.6 with some fixes.
git checkout 3df0e2370d9752801ac744b11307b14e16743a44
# Won't apply automatically due to tab hell.
# https://superuser.com/questions/607410/how-to-copy-paste-tab-characters-via-the-clipboard-into-terminal-session-on-gnom
git apply <<'EOS'
diff --git a/3rdparty/ff-petsc/Makefile b/3rdparty/ff-petsc/Makefile
index dc62ab06..13cd3253 100644
--- a/3rdparty/ff-petsc/Makefile
+++ b/3rdparty/ff-petsc/Makefile
@@ -204,7 +204,7 @@ $(SRCDIR)/tag-make-real:$(SRCDIR)/tag-conf-real
$(SRCDIR)/tag-install-real :$(SRCDIR)/tag-make-real
cd $(SRCDIR) && $(MAKE) PETSC_DIR=$(PETSC_DIR) PETSC_ARCH=fr install
-test -x "`type -p otool`" && make changer
- cd $(SRCDIR) && $(MAKE) PETSC_DIR=$(PETSC_DIR) PETSC_ARCH=fr check
+ #cd $(SRCDIR) && $(MAKE) PETSC_DIR=$(PETSC_DIR) PETSC_ARCH=fr check
test -e $(DIR_INSTALL_REAL)/include/petsc.h
test -e $(DIR_INSTALL_REAL)/lib/petsc/conf/petscvariables
touch $@
@@ -293,7 +293,6 @@ $(SRCDIR)/tag-tar:$(PACKAGE)
-tar xzf $(PACKAGE)
patch -p1 < petsc-hpddm.patch
ifeq ($(WIN32DLLTARGET),)
- patch -p1 < petsc-metis.patch
endif
touch $@
$(PACKAGE):
EOS
autoreconf -i
./configure --enable-download --enable-optim --prefix="$(pwd)/../FreeFem-install"
./3rdparty/getall -a
cd 3rdparty/ff-petsc
make petsc-slepc
cd -
./reconfigure
make -j`nproc`
make install
cd ../FreeFem-install
PATH="${PATH}:$(pwd)/bin" ./bin/FreeFem++ ../FreeFem-sources/examples/tutorial/Ciro's initial build experience was a bit painful, possibly because it was done on a relatively new Ubuntu 20.04 as of June 2020, but in the end it worked: github.com/FreeFem/FreeFem-sources/issues/141
The main/only dependency appears to be PETSc which is used by default, which is a good sign, as that library appears to automatically parallelize a single input to several backends (single CPU, MPI, GPU) so you know things will scale up as you reach simulations.
The problem is that it compiling such a complex dependency opens up much more room for hard to solve compilation errors, and takes a lot more time.
One big advantage over FreeFem is that it uses plain old Python to describe the problems instead of a domain-specific language. Matplotlib is used for plotting by default, so we get full Python power out of the box!
One downside is that its documentation is a Springer published PDF link.springer.com/content/pdf/10.1007%2F978-3-319-52462-7.pdf which is several years out-of-date (tested with FEnics 2016.2. Newbs. This causes problems e.g.: stackoverflow.com/questions/53730427/fenics-did-not-show-figure-nameerror-name-interactive-is-not-defined/57390687#57390687
system of partial differential equations are mentioned at: link.springer.com/content/pdf/10.1007%2F978-3-319-52462-7.pdf 3.5 "A system of advection–diffusion–reaction equations". You don't need to manually iterate between the equations.
On Ubuntu 20.04 as per fenicsproject.org/download/Before 2020-06, it was failing with:but they seem to have created the Ubuntu 20.04 package as of 2020-06, so it now worked! askubuntu.com/questions/866901/what-can-i-do-if-a-repository-ppa-does-not-have-a-release-file
sudo apt-get install software-properties-common
sudo add-apt-repository ppa:fenics-packages/fenics
sudo apt-get update
sudo apt-get install --no-install-recommends fenics
sudo apt install fenics
python3 -m pip install -u matplotlibE: The repository 'http://ppa.launchpad.net/fenics-packages/fenics/ubuntu focal Release' does not have a Release file.GitHub account: github.com/hplgit
It should be mentioned that when you start Googling for PDE stuff, you will reach Han's writings a lot under his GitHub Pages: hplgit.github.io/, and he is one of the main authors of the FEniCS Project.
He also published to GitHub pages with his own crazy markdown-like multi-output markup language: github.com/hplgit/doconce.
Rest in peace, Hans.
In many important applications, what you have to solve is not just a single partial differential equation, but multiple partial differential equations coupled to each other. This is the case for many key PDEs including:
One major application of this classification is that different boundary conditions are suitable for different types of partial differential equations as explained at: which boundary conditions lead to existence and uniqueness of a second order PDE.
Bibliography:
www.cns.gatech.edu/~predrag/courses/PHYS-6124-12/StGoChap6.pdf 6.1 "Classification of PDE's" clarifies which boundary conditions are needed for existence and uniqueness of each type of second order of PDE:
This idea comes up particularly in the phase space coordinate of Hamiltonian mechanics.
Basically a subset of the boundary condition for when one of the parameters is time and we are specifying values for the time 0.
Specifies fixed values.
Can be used for elliptic partial differential equations and parabolic partial differential equations.
Numerical examples:
Specifies the derivative in a direction normal to the boundary.
Can be used for elliptic partial differential equations and parabolic partial differential equations.
Sets both a Dirichlet boundary condition and a Neumann boundary condition for a single part of the boundary.
Can be used for hyperbolic partial differential equations.
We understand intuitively that this imposes stricter requirements on solutions, which makes it easier to guarantee uniqueness, but also harder to have existence. TODO intuitively why hyperbolic need this extra level of restriction.
Linear combination of a Dirichlet boundary condition and Neumann boundary condition at each point of the boundary.
Examples:
- In this case, the normal derivative at the boundary is proportional to the difference between the temperature of the boundary and the fixed temperature of the external environment.The result as time tends to infinity is that the temperature of the plaque tends to that of the environment.
In the context of wave-like equations, an open-boundary condition is one that "lets the wave go through without reflection".
This condition is very useful when we want to simulate infinite domains with a numerical method. Ciro Santilli wants to do this all the time when trying to come up with demos for his physics writings.
Here are some resources that cover such boundary conditions:
- www.asc.tuwien.ac.at/~arnold/pdf/graz/graz.pdf lots of slides
- hplgit.github.io/wavebc/doc/pub/._wavebc_cyborg002.html mentions them and gives a 1D formula. It mentions that things get complicated in 2D and 3D TODO why.The other page: hplgit.github.io/wavebc/doc/pub/._wavebc_cyborg003.html shows solution demos.
Multiple boundary conditions for different parts of the boundary.
Most commonly, boundary conditions such as the Dirichlet boundary condition are taken to be fixed values in time.
Some bibliography:
This basically adds one more ingredient to partial differential equations: a function that we can select.
And then the question becomes: if this function has such and such limitation, can we make the solution of the differential equation have such and such property?
Control theory also takes into consideration possible discretization of the domain, which allows using numerical methods to solve partial differential equations, as well as digital, rather than analogue control methods.
Articles by others on the same topic
There are currently no matching articles.