Brazilian exchange students Updated 2025-07-16
Circle Updated 2025-07-16
Geographical division of the United Kingdom Updated 2025-07-16
Software-based artificial life Updated 2025-07-16
Ciro Santilli just always feels that what can be classified as "artificial life" simulators have too much focus on beating more continuous population mechanics, and lack the discrete elements which he feels could be important to AGI: Section "The missing link between continuous and discrete AI".
There is great interest in this direction of research however quite clearly.
Synapsid Updated 2025-07-16
Ciro Santilli's naughty projects Updated 2025-07-16
If Ciro Santilli weren't a natural born activist, he chould have made an excellent intelligence analyst! See also: Section "Being naughty and creative are correlated".
- Stack Overflow Vote Fraud Script
- GitHub makes Ciro feel especially naughty:
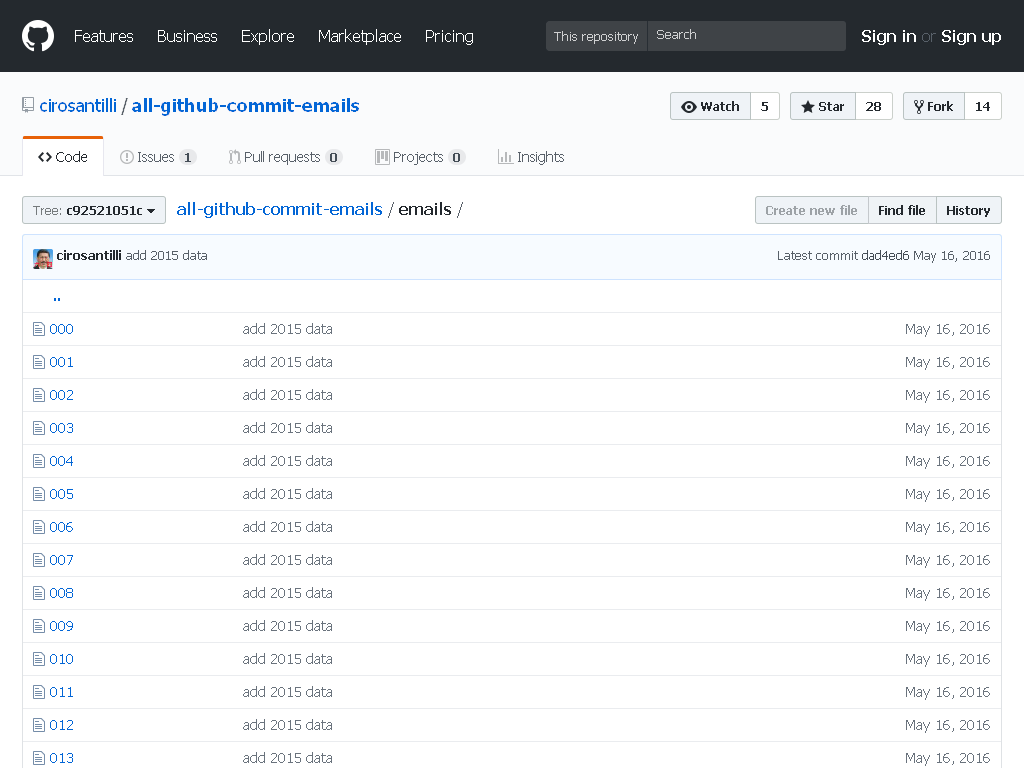
- All GitHub Commit Emails: he extracted (almost) all Git commit emails from GitHub with Google BigQuery
Figure 1. All GitHub Commit Emails repo before takedown. Screenshot from archive.is. - A repository with 1 million commits: likely the live repo with the most commits as of 2017
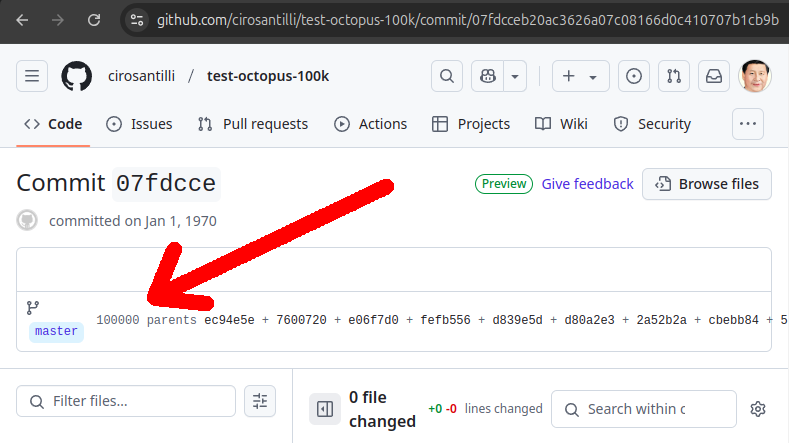
- An 100 year GitHub streak, likely longest ever when that existed. It was consuming too much server resources however, which led to GitHub admins manually turning off his contribution history.
Figure 3. Screenshot of a commit with 100k parents on GitHub. URL: github.com/cirosantilli/test-octopus-100k/commit/07fdcceb20ac3626a07c08166d0c410707b1cb9b- 500 on adoc infinite header xref recursion: that was fun while it lasted
Species bootstrapping from DNA Updated 2025-07-16
Synthesizing the DNA itself is not the only problem however.
You then have to get that DNA into a working living form state so that normal cell processes can continue:
Multicellular questions:
Apparently achieved for the first time in 2021: www.jcvi.org/research/first-self-replicating-synthetic-bacterial-cell by the J. Craig Venter Institute.
Thymine Updated 2025-07-16
Single page application Updated 2025-07-16
Ciro Santilli's selfish desires Updated 2025-07-16
Just enough money to raise 3 kids in a rich country without having to work (so he can focus on whatever project he wants) and no more. Then maximize fame.
Fame is slightly convertible into money with generally little liquidity, but is more valuable if money becomes useless in a TEOTWAWKI.
Of course, in the end, one just does whatever seems cool and useful, and the Gods decide what proportion of fame/money/power they will get. Due to Ciro's love of open source software however, a higher fame percentage seems more likely than money.
Searching just for just "Santilli" on Google does not give any Ciro Santilli hits. The name appears to be a minor variation of the much more common "Santini". Since the name is not that common, it is possible to go over all noteworthy hits. Some relevant ones are shown at: interesting members of the Santilli family.
Searching just for just "Ciro" on Google does not give any Ciro Santilli hits, mostly some smaller brands that could be beaten, this is Ciro's main initial fame metric goal. Reaching it would require doing things known much beyond the programming community however, as Ciro has done until of 2019. ciro.com is from an electromechanics consultancy as of 2019, so it's not bad, let them be.
At the next useless gamified level, an honorary OBE and more ambitiously ForMemRS from the Royal Society post nominal letters would be nice.
The ultimate dream however would be to beat Cyrus the Great himself on Google searches ("Ciro" == "Cyrus" in Portuguese), maybe becoming "Cyrus the Greater"? That one will be a bit harder though. Maybe if Falung Gong becomes the dominant religion in 2000 years like Christianism did, catapulting the Judaism benefactor Cyrus into greater fame, then there is some hope for Ciro as well.
Favela Updated 2025-07-16
Lifegard problem Updated 2025-07-16
Lightweight markup language Updated 2025-07-16
Light year Updated 2025-07-16
Ciro's Edict #5
\Include and \x and working on dynamic website Updated 2025-07-16This was the major final step of fully integrating the OurBigBook CLI into the dynamic website (besides fixing some nasty bugs that escaped passed by me from the previous newsletter).
Ciro Santilli's sport practice Updated 2025-07-16
As a Brazilian, Ciro Santilli used to really love playing soccer (but not watching it), until he hurt his knee.
Playing soccer just feels amazing, because you are constantly running around, but with a more specific goal in mind: to get that ball into that goal!
Playing soccer was specially amazing in the flat wet sand beach of Santos. weekend, the sea, feet touching the sand, the sun going down, and your school mates next to you. Nirvana.
It is also true that under those conditions, the skin of your feet will get ripped off due to running on the slightly wet and flat sand no matter how thick it has become. But it is worth it.
Teams would often be slit between "the team with shirts vs the team without shirts", who would just take off their shirts. The two best players would take turns picking players into their teams, the first one to pick would be decided by odds and evens (par ou ímpar).
A pair of Havaianas, or Havaianas rip-offs, stuck into the sand, or even just some school bags, would do as a goal posts. More organized people, especially adults, would have their own water pipe goal with a proper net and all. But doing so would spoil the fun of endless discussions if a non flat ball had gone in or not into an imaginary rectangle.
That's how soccer was meant to be played.
Ciro hates water, so swimming is out of the question. What could be more boring than going back and forth on a fixed location a million times to gain some milliseconds?
Running would have been a consideration, but Ciro Santilli's legs sometimes itch when he runs.
This is until he ended up living in a place with decent roads for cycling in the late 2010's, which led to Ciro Santilli's cycling.
City in Japan Updated 2025-07-16
City in Taiwan Updated 2025-07-16
City of London Updated 2025-07-16
The City of London is an obscene thing. Its existence goes against the will of the greater part of society. All it takes is one glance to see how it is but a bunch of corruption. See e.g.: The Spiders' Web: Britain's Second Empire.
Unlisted articles are being shown, click here to show only listed articles.