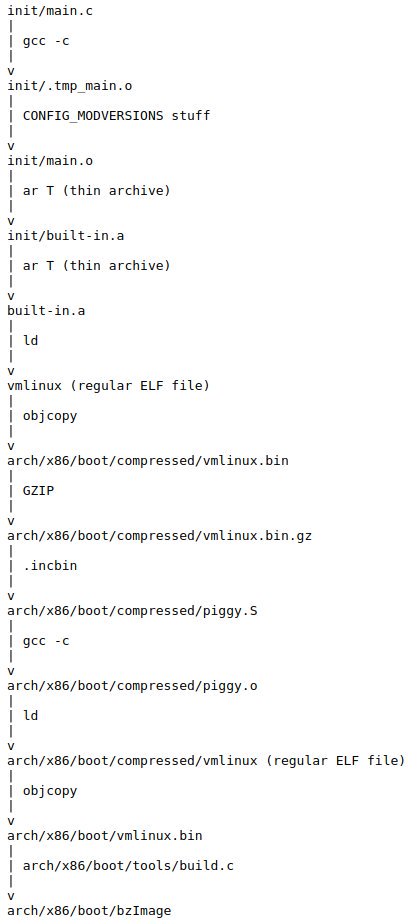
Home Updated 2025-12-02
Check out: OurBigBook.com, the best way to publish your scientific knowledge. It's an open source note taking system that can publish from lightweight markup files in your computer both to a multi-user mind melding dynamic website, or as a static website. It's like Wikipedia + GitHub + Stack Overflow + Obsidian mashed up. Source code: github.com/ourbigbook/ourbigbook.
Sponsor me to work on this project. For 400k USD I will quit my job or not get a new job and work on OurBigBook full time for a second year to try and kickstart The Higher Education Revolution. Status: ~44k / 400k USD. At 4M USD I retire/tenure and work on open STEM forever. How to donate: Section "Sponsor Ciro Santilli's work on OurBigBook.com".
I first quit my job 1st June 2024 to work on the project for 1 year after I reached my initial 100k goal mostly via a 1000 Monero donation. For a second follow up year, I increased my requirement to 400k USD to give me more peace of mind as I'm destroying my career in the process. A second year greatly improve chances of success: on year one I improved my tech, on year two I want to come guns blazing to solve courses and get users.
Mission: to live in a world where you can learn university-level mathematics, physics, chemistry, biology and engineering from perfect free open source books that anyone can write to get famous. More rationale: Section "OurBigBook.com"
Explaining things is my superpower, e.g. I was top user #39 on Stack Overflow in 2023[ref][ref] and I have a few 1k+ star educational GitHub repositories[ref][ref][ref][ref]. Now I want to bring that level of awesomeness to masters level Mathematics and Physics. But I can't do it alone! So I created OurBigBook.com to allow everyone to work together towards the perfect book of everything.
My life's goal is to bring hardcore university-level STEM open educational content to all ages. Sponsor me at github.com/sponsors/cirosantilli starting from 1$/month so I can work full time on it. Further information: Section "Sponsor Ciro Santilli's work on OurBigBook.com". Achieving what I call "free gifted education" is my Nirvana.
This website is written in OurBigBook Markup, and it is published on both cirosantilli.com (static website) and outbigbook.om/cirosantilli (multi-user OurBigBook Web instance). Its source code is located at: github.com/cirosantilli/cirosantilli.github.io and also at
cirosantilli.com/_dir and it is licensed under CC BY-SA 4.0 unless otherwise noted.To contact Ciro, see: Section "How to contact Ciro Santilli". He likes to talk with random people of the Internet.
GitHub | Stack Overflow | LinkedIn | YouTube | Twitter | Wikipedia | Zhihu 知乎 | Weibo 微博 | Other accounts
Besides that, I'm also a freedom of speech slacktivist and recreational cyclist. I like Chinese traditional music and classic Brazilian pop. Opinions are my own, but they could be yours too. Tax the rich.
Let's create an educational system with:
- no distinction between university and high school, students just go as fast as they can to what they really want without stupid university entry exams
- fully open source learning material
- on-demand examinations that anyone can easily take without prerequisites
- granular entry selection only for space in specific laboratories or participation in specific novel research projects
I offer:
- online private tutoring for:
- any STEM university course
- passionate younger STEM students (any age) who want to learn university level material and beyond. Can your kid be the next Fields Medalist or Nobel Prize winner? I'm here to help, especially if you are filthy rich! I focus moving students forward as fast as they want on and on producing useful novel tutorials and results
Let your child be my Emile, and me be their Adolfo Amidei, and let's see how far they can go! I will help take your child:and achieve their ambitious STEM goals!- into the best universities
- into the best PhD programs
- educational consulting for institutions looking to improve their STEM courses
- do you know that course or teacher that consistently gets bad reviews every year? I'll work with the teacher to turn the problem around!
- are you looking to create a consistent open educational resources offering to increase your institutions internationally visibility? I can help with that too.
My approach is to:For minors, parents are welcome to join video calls, and all interactions with the student will be recorded and made available to parents.
- propose interesting research projects. The starting point is always deciding the end goal: Section "Backward design"
- learn what is needed to do the project together with the student(s)
- publish any novel results or tutorials/tools produced freely licensed online, and encourage the student to do the same (Section "Let students learn by teaching", digital garden)
I have a proven track of explaining complex concepts in an interesting and useful way. I work for the learner. Teaching statement at: Section "How to teach". Pricing to be discussed. Contact details at: Section "How to contact Ciro Santilli".
I am particularly excited about pointing people to the potential next big things, my top picks these days are:I am also generally interested in:
- quantum computing
- AGI research, in particular AI code generation, automated theorem proving and robotics
- assorted molecular biology technologies
- 20th century physics, notably AMO and condensed matter
- the history of science, and in particular trying to look at seminal papers of a field
Ciro Santilli's amazing Stack Overflow profile
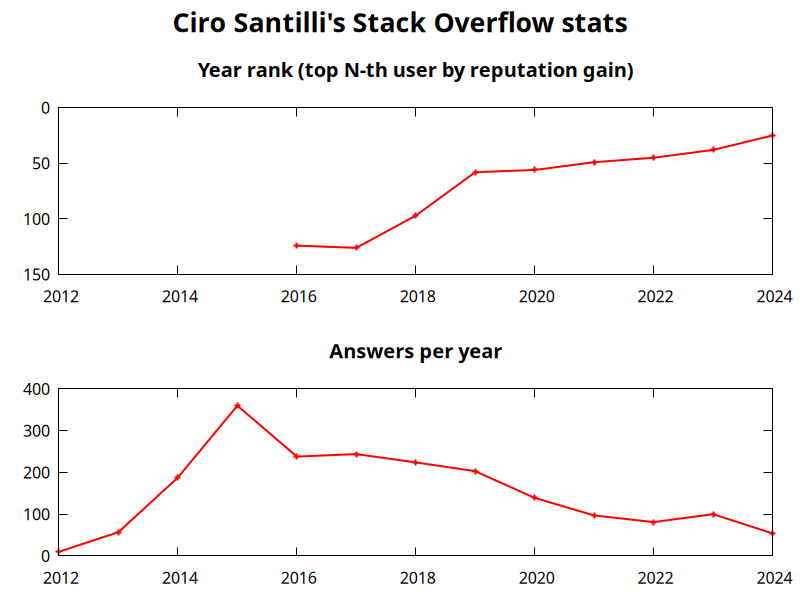
. Ciro contributes almost exclusively by answering question he Googles into out of his own need, and never by refreshing the newest question of big tags for low hanging fruit! More information at: Section "Ciro Santilli's Stack Overflow contributions".Ciro Santilli's Stack Overflow stats
. Further methodology details at: Figure "Ciro Santilli's Stack Overflow stats".The problem with education by Ciro Santilli
. Source. In this video Ciro Santilli exposes his fundamental philosophy regarding why Education is broken. This philosophy was the key motivation behind the failed OurBigBook Project.OurBigBook Web topics demo
. Source. The OurBigBook topic feature allows users to "merge their minds" in a "sort by upvote"-stack overflow-like manner for each subject. This is the killer feature of OurBigBook Web. More information at: docs.ourbigbook.com/ourbigbook-web-topics.OurBigBook dynamic article tree demo
. Source. The OurBigBook dynamic tree feature allows any of your headers to be the toplevel h1 header of a page, while still displaying its descendants. SEO loves this, and it also allows users to always get their content on the correct granularity. More information at: docs.ourbigbook.com/ourbigbook-web-dynamic-article-tree.OurBigBook local editing and publishing demo
. Source. With OurBigBook you can store your content as plaintext files in a Lightweight markup, and then publish that to either OurBigBook.com to get awesome multi-user features, or as a static website where you are in full control. More information at: docs.ourbigbook.com/publish-your-content.Top Down 2D continuous game with Urho3D C++ SDL and Box2D for Reinforcement learning by Ciro Santilli (2018)
Source. More information: Section "Ciro's 2D reinforcement learning games". This is Ciro's underwhelming stab at the fundamental question: Can AGI be trained in simulations?. This project could be taken much further.Water Margin tribute to Chinese dissidents by Ciro Santilli (2022)
Source. Part of Ciro Santilli's campaign for freedom of speech in China, see also: cirosantilli.com/china-dictatorship/water-margin.Lenovo ThinkPad T430 running a BIOS hello world
. This uses Ciro Santilli's project x86 bare metal examples with source code at: github.com/cirosantilli/x86-bare-metal-examplesLinux Kernel Module Cheat presentation
. Source. This project, with source code at: github.com/cirosantilli/linux-kernel-module-cheat, aims to be the perfect emulation setup to study and develop the Linux kernel, kernel modules, QEMU, gem5 as well as x86_64, ARM userland and baremetal assembly and more.My Bitcoin inscription museum by Ciro Santilli
. Source. Introductory video to Section "Cool data embedded in the Bitcoin blockchain". -------------------------------------
| Force of Will 3 U U |
| --------------------------------- |
| | //////////// | |
| | ////() ()\////\ | |
| | ///_\ (--) \///\ | |
| | ) //// \_____///\\ | |
| | ) \ / / / / | |
| | ) / \ | | / _/ | |
| | ) \ ( ( / / / / \ | |
| | / ) ( ) / ( )/( ) \ | |
| | \(_)/(_)/ /UUUU \ \\\/ | | |
| .---------------------------------. |
| Interrupt |
| ,---------------------------------, |
| | You may pay 1 life and remove a | |
| | blue card in your hand from the | |
| | game instead of paying Force of | |
| | Will's casting cost. Effects | |
| | that prevent or redirect damage | |
| | cannot be used to counter this | |
| | loss of life. | |
| | Counter target spell. | |
| `---------------------------------` |
| l
| Illus. Terese Nelsen |
-------------------------------------Code 1.
ASCII art of a Force of Will Magic: The Gathering card inscribed in the Bitcoin blockchain
. Artist unknown, uploaded December 2014. Part of Section "Cool data embedded in the Bitcoin blockchain" where Ciro Santilli maintains a curated list of such interesting inscriptions.
This was a small project done by Ciro for artistic purposes that received some attention due to the incredible hype surrounding cryptocurrencies at the time. Ciro Santilli's views on cryptocurrencies are summarized at: Section "Are cryptocurrencies useful?".
YellowRobot.jpgJPG image fully embedded in the Bitcoin blockchain depicting some kind of cut material art depicting a yellow robot, inscribed on January 29, 2017.
Ciro Santilli found this image and others during his research for Section "Cool data embedded in the Bitcoin blockchain" by searching for image fingerprints on every transaction payload of the blockchain with a script.
The image was uploaded by EMBII, co-creator of the AtomSea & EMBII upload mechanism, which was responsible for a large part of the image inscriptions in the Bitcoin blockchain.
The associated message reads:This is one of Ciro Santilli's favorite AtomSea & EMBII uploads, as it perfectly encapsules the "medium as an art form" approach to blockchain art, where even non-novel works can be recontextualized into something interesting, here depicting an opposition between the ephemeral and the immutable.
Chiharu [EMBII's Japanese wife] and I found this little yellow robot while exploring Chicago. It will be covered by tar or eventually removed but this tribute will remain. N 41.880778 E -87.629210
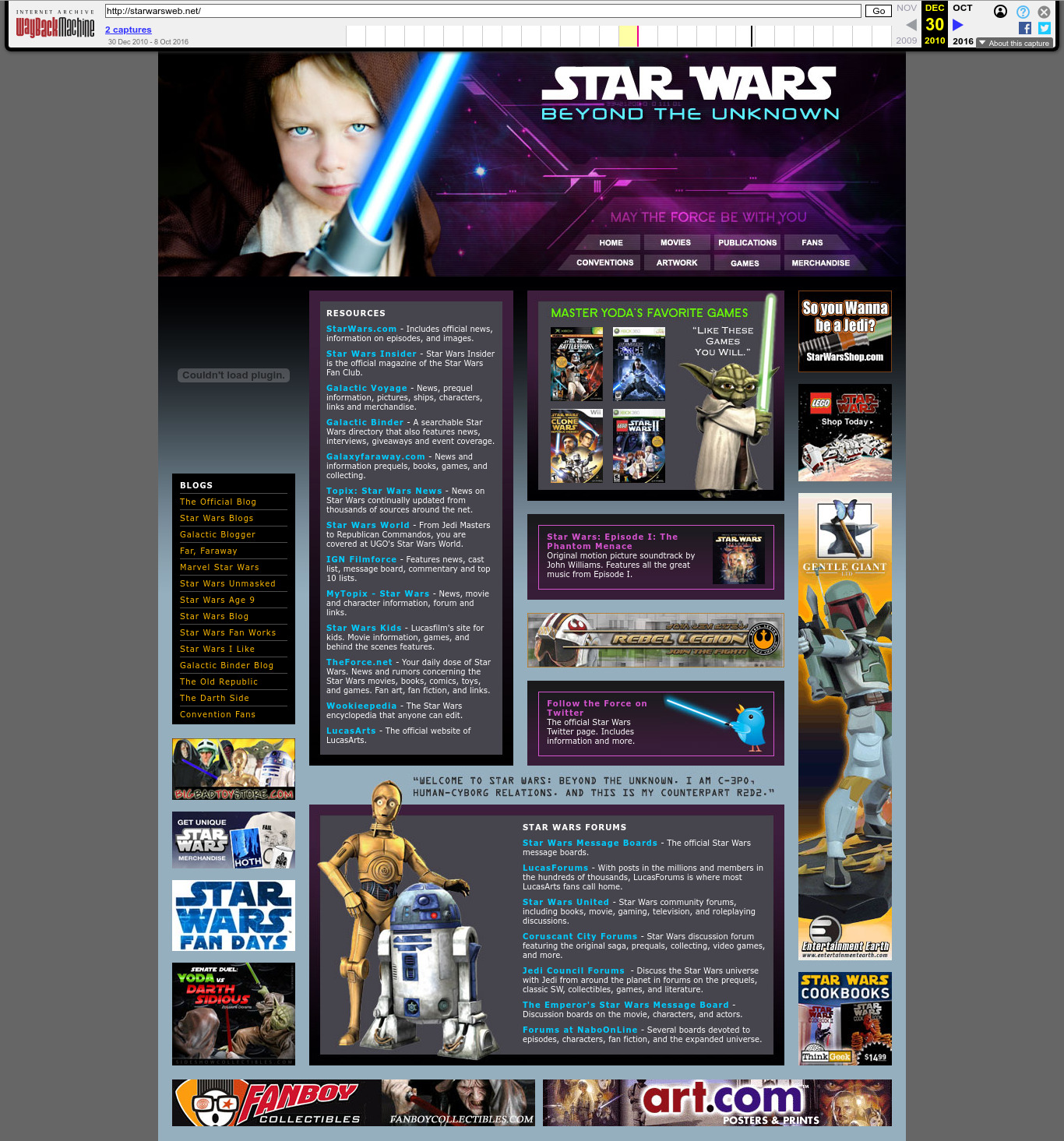
2010 Wayback Machine archive of starwarsweb.net
. This website was used as one of the CIA 2010 covert communication websites, a covert system the CIA used to communicate with its assets. More details at: Section "CIA 2010 covert communication websites".
Ciro Santilli had some naughty OSINT fun finding some of the websites of this defunct network in 2023 after he heard about the 2022 Reuters report on the matter, which for the first time gave away 7 concrete websites out of a claimed 885 total found. As of November 2023, Ciro had found about 350 of them.
2010 Wayback Machine archive of noticiasmusica.net
. This is another website that was used as one of the CIA 2010 covert communication websites. This website is written in Brazilian Portuguese, and therefore suggests that the CIA had assets in Brazil at the time, and thus was spying on a "fellow democracy".
Although Snowden's revelations made it extremely obvious to the world that the USA spies upon everyone outside of the Five Eyes, including fellow democracies, it is rare to have such a direct a concrete proof of it visible live right on the Wayback Machine. Other targeted democracies include France, Germany, Italy and Spain. More details at: USA spying on its own allies.
This investigative report by Ciro Santilli was featured on the Daily Mail after 404 Media reported on it in 2025.
Diagram of the fundamental theorem on homomorphisms by Ciro Santilli (2020)
Shows the relationship between group homomorphisms and normal subgroups.
Used in the Stack Exchange answer to What is the intuition behind normal subgroups? One of Section "The best articles by Ciro Santilli".
Spacetime diagram illustrating how faster-than-light travel implies time travel by Ciro Santilli (2021)
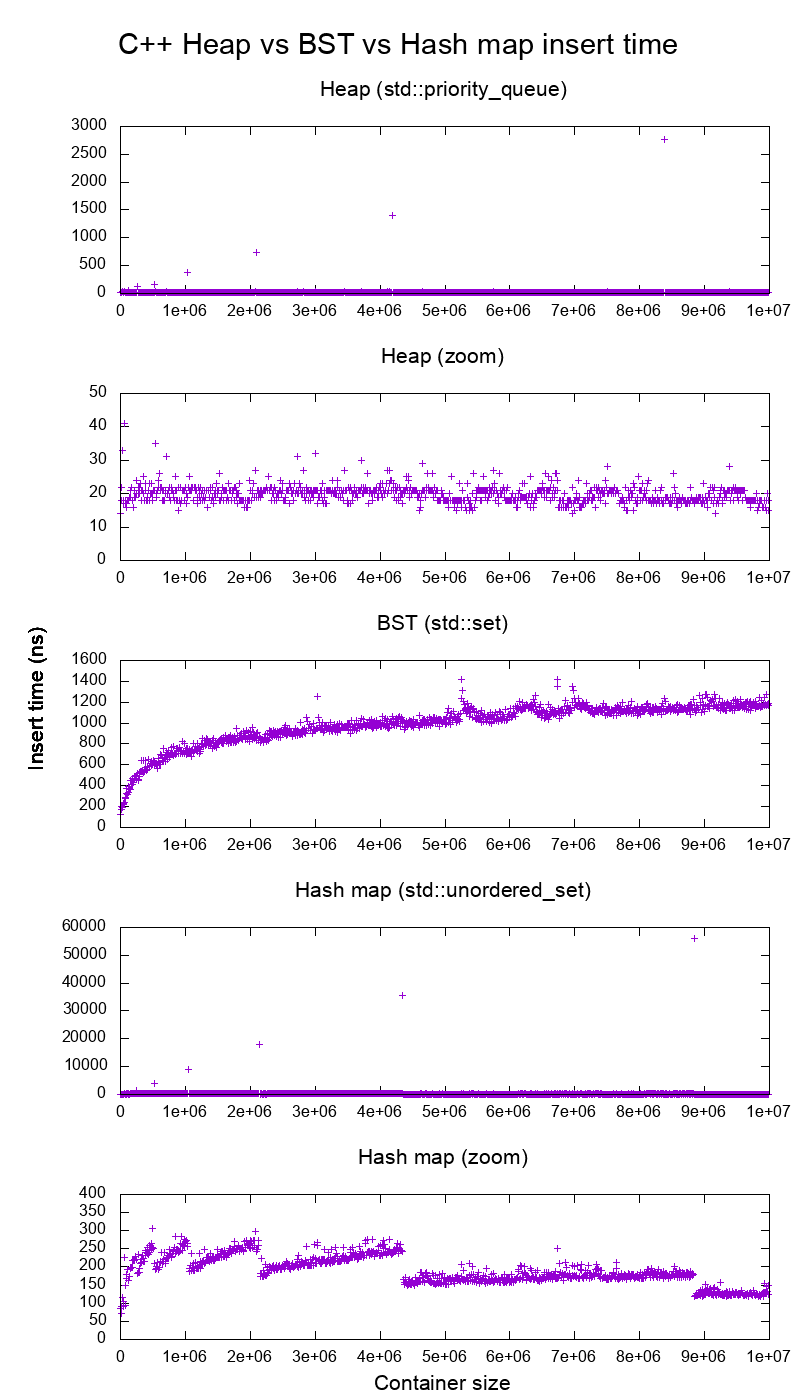
Used in the Stack Exchange answer to Does faster than light travel imply travelling back in time?. One of Section "The best articles by Ciro Santilli".Average insertion time into heaps, binary search tree and hash maps of the C++ standard library by Ciro Santilli (2015)
Source. Used in the Stack Overflow answer to Heap vs Binary Search Tree (BST). One of Section "The best articles by Ciro Santilli".Birch and Swinnerton-Dyer conjecture in two minutes by Ciro Santilli
. Source. Quick and direct explanation of the statement of the BSD conjecture for people who know basic university mathematics. This is one of the Millennium Prize Problems, and you will get a million dollars if you can solve it! This therefore falls in the Simple to state but hard to prove of Ciro Santilli's the beauty of mathematics aesthetics.Top view of an open Oxford Nanopore MinION
. Source. This is Ciro Santilli's hand on the Wikipedia article: en.wikipedia.org/wiki/Oxford_Nanopore_Technologies. He put it there after working a bit on Section "How to use an Oxford Nanopore MinION to extract DNA from river water and determine which bacteria live in it" :-) And he would love to document more experiments like that one Section "Videos of all key physics experiments", but opportunities are extremely rare.A quick 2D continuous AI game prototype for reinforcement learning written in Matter.js, you can view it on a separate page at cirosantilli.com/_raw/js/matterjs/examples.html#top-down-asdw-fixed-viewport. This is a for-fun-only prototype for Ciro's 2D reinforcement learning games, C++ or maybe Python (for the deep learning ecosystem) seems inevitable for a serious version of such a project. But it is cute how much you can do with a few lines of Matter.js!
HTML snippet:
<iframe src="_raw/js/matterjs/examples.html#top-down-asdw-fixed-viewport" width="1000" height="850"></iframe> The best articles by Ciro Santilli Updated 2025-07-16
These are the best articles ever authored by Ciro Santilli, most of them in the format of Stack Overflow answers.
Ciro posts update about new articles on his Twitter accounts.
Some random generally less technical in-tree essays will be present at: Section "Essays by Ciro Santilli".
- Trended on Hacker News:
- CIA 2010 covert communication websites on 2023-06-11. 190 points, a mild success.
- x86 Bare Metal Examples on 2019-03-19. 513 points. The third time something related to that repo trends. Hacker news people really like that repo!
- again 2020-06-27 (archive). 200 points, repository traffic jumped from 25 daily unique visitors to 4.6k unique visitors on the day
- How to run a program without an operating system? on 2018-11-26 (archive). 394 points. Covers x86 and ARM
- ELF Hello World Tutorial on 2017-05-17 (archive). 334 points.
- x86 Paging Tutorial on 2017-03-02. Number 1 Google search result for "x86 Paging" in 2017-08. 142 points.
- x86 assembly
- What does "multicore" assembly language look like?
- What is the function of the push / pop instructions used on registers in x86 assembly? Going down to memory spills, register allocation and graph coloring.
- Linux kernel
- What do the flags in /proc/cpuinfo mean?
- How does kernel get an executable binary file running under linux?
- How to debug the Linux kernel with GDB and QEMU?
- Can the sys_execve() system call in the Linux kernel receive both absolute or relative paths?
- What is the difference between the kernel space and the user space?
- Is there any API for determining the physical address from virtual address in Linux?
- Why do people write the
#!/usr/bin/envpython shebang on the first line of a Python script? - How to solve "Kernel Panic - not syncing: VFS: Unable to mount root fs on unknown-block(0,0)"?
- Single program Linux distro
- QEMU
- gcc and Binutils:
- How do linkers and address relocation works?
- What is incremental linking or partial linking?
- GOLD (
-fuse-ld=gold) linker vs the traditional GNU ld and LLVM ldd - What is the -fPIE option for position-independent executables in GCC and ld? Concrete examples by running program through GDB twice, and an assembly hello world with absolute vs PC relative load.
- How many GCC optimization levels are there?
- Why does GCC create a shared object instead of an executable binary according to file?
- C/C++: almost all of those fall into "disassemble all the things" category. Ciro also does "standards dissection" and "a new version of the standard is out" answers, but those are boring:
- What does "static" mean in a C program?
- In C++ source, what is the effect of
extern "C"? - Char array vs Char Pointer in C
- How to compile glibc from source and use it?
- When should
static_cast,dynamic_cast,const_castandreinterpret_castbe used? - What exactly is
std::atomicin C++?. This answer was originally more appropriately entitled "Let's disassemble some stuff", and got three downvotes, so Ciro changed it to a more professional title, and it started getting upvotes. People judge books by their covers. notmain.o 0000000000000000 0000000000000017 W MyTemplate<int>::f(int) main.o 0000000000000000 0000000000000017 W MyTemplate<int>::f(int)Code 1.. From: What is explicit template instantiation in C++ and when to use it?nmoutputs showing that objects are redefined multiple times across files if you don't use template instantiation properly
- IEEE 754
- What is difference between quiet NaN and signaling NaN?
- In Java, what does NaN mean?
Without subnormals: +---+---+-------+---------------+-------------------------------+ exponent | ? | 0 | 1 | 2 | 3 | +---+---+-------+---------------+-------------------------------+ | | | | | | v v v v v v ----------------------------------------------------------------- floats * **** * * * * * * * * * * * * ----------------------------------------------------------------- ^ ^ ^ ^ ^ ^ | | | | | | 0 | 2^-126 2^-125 2^-124 2^-123 | 2^-127 With subnormals: +-------+-------+---------------+-------------------------------+ exponent | 0 | 1 | 2 | 3 | +-------+-------+---------------+-------------------------------+ | | | | | v v v v v ----------------------------------------------------------------- floats * * * * * * * * * * * * * * * * * ----------------------------------------------------------------- ^ ^ ^ ^ ^ ^ | | | | | | 0 | 2^-126 2^-125 2^-124 2^-123 | 2^-127Code 2.Visualization of subnormal floating point numbers vs what IEEE 754 would look like without them. From: What is a subnormal floating point number?
- Computer science
- Algorithms
Figure 5. Average insertion time into heaps, binary search tree and hash maps of the C++ standard library. Source. From: Heap vs Binary Search Tree (BST)
- Is it necessary for NP problems to be decision problems?
- Polynomial time and exponential time. Answered focusing on the definition of "exponential time".
- What is the smallest Turing machine where it is unknown if it halts or not?. Answer focusing on "blank tape" initial condition only. Large parts of it are summarizing the Busy Beaver Challenge, but some additions were made.
- Algorithms
- Git
| 0 | 4 | 8 | C | |-------------|--------------|-------------|----------------| 0 | DIRC | Version | File count | ctime ...| 0 | ... | mtime | device | 2 | inode | mode | UID | GID | 2 | File size | Entry SHA-1 ...| 4 | ... | Flags | Index SHA-1 ...| 4 | ... |Code 3.ASCII art depicting the binary file format of the Git index file. From: What does the git index contain EXACTLY?tree {tree_sha} {parents} author {author_name} <{author_email}> {author_date_seconds} {author_date_timezone} committer {committer_name} <{committer_email}> {committer_date_seconds} {committer_date_timezone} {commit message}Code 4.Description of the Git commit object binary data structure. From: What is the file format of a git commit object data structure?- How do I clone a subdirectory only of a Git repository?
- Python
- Web technology
- OpenGL
Figure 7. OpenGL rendering output dumped to a GIF file. Source. From: How to use GLUT/OpenGL to render to a file?- What are shaders in OpenGL?
- Why do we use 4x4 matrices to transform things in 3D?
Figure 10. Sinusoidal circular wave heatmap generated with an OpenGL shader at 60 FPS on SDL. Source.
- Node.js
- Ruby on Rails
- POSIX
- What is POSIX? Huge classified overview of the most important things that POSIX specifies.
- Systems programming
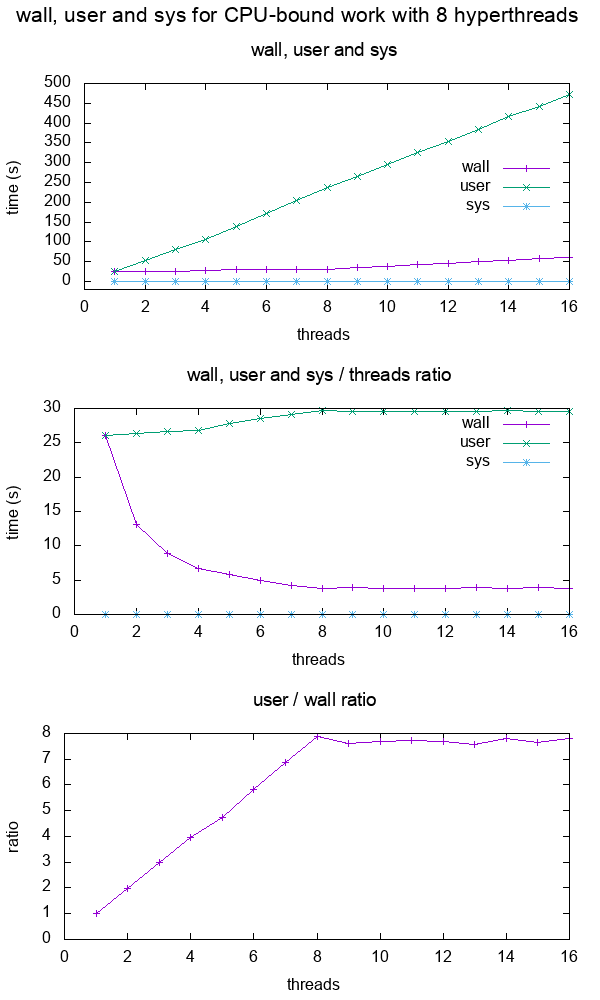
- What do the terms "CPU bound" and "I/O bound" mean?
Figure 12. Plot of "real", "user" and "sys" mean times of the output of time for CPU-bound workload with 8 threads. Source. From: What do 'real', 'user' and 'sys' mean in the output of time?+--------+ +------------+ +------+ | device |>---------------->| function 0 |>----->| BAR0 | | | | | +------+ | |>------------+ | | | | | | | +------+ ... ... | | |>----->| BAR1 | | | | | | +------+ | |>--------+ | | | +--------+ | | ... ... ... | | | | | | | | +------+ | | | |>----->| BAR5 | | | +------------+ +------+ | | | | | | +------------+ +------+ | +--->| function 1 |>----->| BAR0 | | | | +------+ | | | | | | +------+ | | |>----->| BAR1 | | | | +------+ | | | | ... ... ... | | | | | | +------+ | | |>----->| BAR5 | | +------------+ +------+ | | | ... | | | +------------+ +------+ +------->| function 7 |>----->| BAR0 | | | +------+ | | | | +------+ | |>----->| BAR1 | | | +------+ | | ... ... ... | | | | +------+ | |>----->| BAR5 | +------------+ +------+Code 5.Logical struture PCIe device, functions and BARs. From: What is the Base Address Register (BAR) in PCIe?
- Electronics
- Raspberry Pi
Figure 13. Raspberry Pi 2 directly connected to a laptop with an Ethernet cable. Image from answer to: How to hook up a Raspberry Pi via Ethernet to a laptop without a router?Figure 14. . Image from answer to: How to hook up a Raspberry Pi via Ethernet to a laptop without a router? Figure 15. . Image from answer to: How to emulate the Raspberry Pi 2 on QEMU? Figure 16. Bare metal LED blinker program running on a Raspberry Pi 2. Image from answer to: How to run a C program with no OS on the Raspberry Pi?
- Raspberry Pi
- Computer security
- Media
Video 2. Canon in D in C. Source.The original question was deleted, lol...: How to programmatically synthesize music?- How to resize a picture using ffmpeg's sws_scale()?
- Is there any decent speech recognition software for Linux? ran a few examples manually on
vosk-apiand compared to ground truth.
- Eclipse
- Computer hardware
- Scientific visualization software
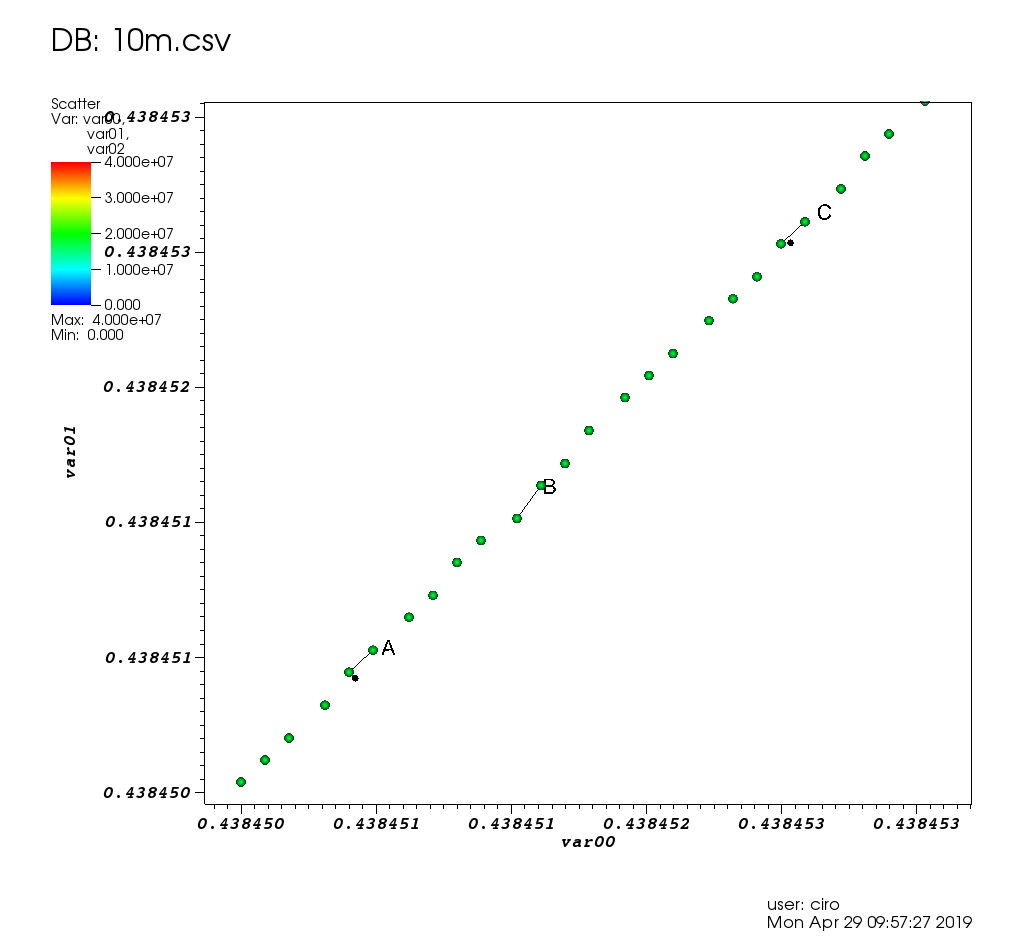
Figure 17. VisIt zoom in 10 million straight line plot with some manually marked points. Source. From: Section "Survey of open source interactive plotting software with a 10 million point scatter plot benchmark by Ciro Santilli"
- Numerical analysis
- Computational physics
- Register transfer level languages like Verilog and VHDL
- Verilog:
Figure 19. . See also: Section "Verilator interactive example"
- Verilog:
- Android
Video 4. Android screen showing live on an Ubuntu laptop through ADB. Source. From: How to see the Android screen live on an Ubuntu desktop through ADB?
- Debugging
- Program optimization
- What is tail call optimization?
Figure 21. . Source. The answer compares gprof, valgrind callgrind, perf and gperftools on a single simple executable.
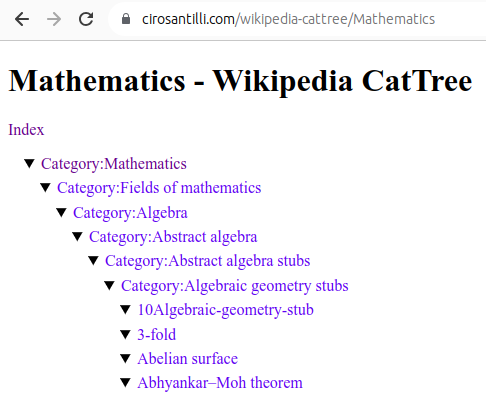
- Data
Figure 22. Mathematics dump of Wikipedia CatTree. Source. In this project, Ciro Santilli explored extracting the category and article tree out of the Wikipedia dumps.
- Mathematics
Figure 23. Diagram of the fundamental theorem on homomorphisms by Ciro Santilli (2020)Shows the relationship between group homomorphisms and normal subgroups.- Section "Formalization of mathematics": some early thoughts that could be expanded. Ciro almost had a stroke when he understood this stuff in his teens.
Figure 24. Simple example of the Discrete Fourier transform. Source. That was missing from Wikipedia page: en.wikipedia.org/wiki/Discrete_Fourier_transform!
- Network programming
- Physics
- What is the difference between plutonium and uranium?
Figure 25. Spacetime diagram illustrating how faster-than-light travel implies time travel. From: Does faster than light travel imply travelling back in time?
- Biology
Figure 26. Top view of an open Oxford Nanopore MinION. Source. From: Section "How to use an Oxford Nanopore MinION to extract DNA from river water and determine which bacteria live in it"Figure 27. Mass fractions in a minimal growth medium vs an amino acid cut in a simulation of the E. Coli Whole Cell Model by Covert Lab. Source. From: Section "E. Coli Whole Cell Model by Covert Lab"
- Quantum computing
- Section "Quantum computing is just matrix multiplication"
Figure 28. Visualization of the continuous deformation of states as we walk around the Bloch sphere represented as photon polarization arrows. From: Understanding the Bloch sphere.
- Bitcoin
- GIMP
Figure 29. GIMP screenshot part of how to combine two images side-by-side in GIMP?
- Home DIY
Figure 30. Total_Blackout_Cassette_Roller_Blind_With_Curtains.Source. From: Section "How to blackout your window without drilling"
- China
Diagonal matrix Updated 2025-07-16
Fundamental theorem on homomorphisms Updated 2025-07-16
Group extension problem Updated 2025-07-16
Besides the understandable Wikipedia definition, Video "Simple Groups - Abstract Algebra by Socratica (2018)" gives an understandable one:
Given a finite group and a simple group , find all groups such that is a normal subgroup of and .
We don't really know how to make up larger groups from smaller simple groups, which would complete the classification of finite groups:
In particular, this is hard because you can't just take the direct product of groups to retrieve the original group: Section "Relationship between the quotient group and direct products".
Group homomorphism Updated 2025-07-16
Like isomorphism, but does not have to be one-to-one: multiple different inputs can have the same output.
This brings us to the key intuition about group homomorphisms: they are a way to split out a larger group into smaller groups that retains a subset of the original structure.
As shown by the fundamental theorem on homomorphisms, each group homomorphism is fully characterized by a normal subgroup of the domain.
Lie algebra Updated 2025-07-16
Like everything else in Lie groups, first start with the matrix as discussed at Section "Lie algebra of a matrix Lie group".
Intuitively, a Lie algebra is a simpler object than a Lie group. Without any extra structure, groups can be very complicated non-linear objects. But a Lie algebra is just an algebra over a field, and one with a restricted bilinear map called the Lie bracket, that has to also be alternating and satisfy the Jacobi identity.
Because of the Lie group-Lie algebra correspondence, we know that there is almost a bijection between each Lie group and the corresponding Lie algebra. So it makes sense to try and study the algebra instead of the group itself whenever possible, to try and get insight and proofs in that simpler framework. This is the key reason why people study Lie algebras. One is philosophically reminded of how normal subgroups are a simpler representation of group homomorphisms.
To make things even simpler, because all vector spaces of the same dimension on a given field are isomorphic, the only things we need to specify a Lie group through a Lie algebra are:Note that the Lie bracket can look different under different basis of the Lie algebra however. This is shown for example at Physics from Symmetry by Jakob Schwichtenberg (2015) page 71 for the Lorentz group.
- the dimension
- the Lie bracket
As mentioned at Lie Groups, Physics, and Geometry by Robert Gilmore (2008) Chapter 4 "Lie Algebras", taking the Lie algebra around the identity is mostly a convention, we could treat any other point, and things are more or less equivalent.
Relationship between the quotient group and direct products Updated 2025-07-16
Although quotients look a bit real number division, there are some important differences with the "group analog of multiplication" of direct product of groups.
If a group is isomorphic to the direct product of groups, we can take a quotient of the product to retrieve one of the groups, which is somewhat analogous to division: math.stackexchange.com/questions/723707/how-is-the-quotient-group-related-to-the-direct-product-group
The "converse" is not always true however: a group does not need to be isomorphic to the product of one of its normal subgroups and the associated quotient group. The wiki page provides an example:
Given G and a normal subgroup N, then G is a group extension of G/N by N. One could ask whether this extension is trivial or split; in other words, one could ask whether G is a direct product or semidirect product of N and G/N. This is a special case of the extension problem. An example where the extension is not split is as follows: Let , and which is isomorphic to Z2. Then G/N is also isomorphic to Z2. But Z2 has only the trivial automorphism, so the only semi-direct product of N and G/N is the direct product. Since Z4 is different from Z2 × Z2, we conclude that G is not a semi-direct product of N and G/N.
This is also semi mentioned at: math.stackexchange.com/questions/1596500/when-is-a-group-isomorphic-to-the-product-of-normal-subgroup-and-quotient-group
I think this might be equivalent to why the group extension problem is hard. If this relation were true, then taking the direct product would be the only way to make larger groups from normal subgroups/quotients. But it's not.
Scalar matrix Updated 2025-07-16
Simple group Updated 2025-07-16
Does not have any non-trivial normal subgroup.
And therefore, going back to our intuition that due to the fundamental theorem on homomorphisms there is one normal group per homomorphism, a simple group is one that has no non-trivial homomorphisms.
Subquotient Updated 2025-07-16
As an overkill example, the happy family are subquotients of the monster group, but the monster group is simple.