The best articles by Ciro Santilli Updated 2025-07-16
These are the best articles ever authored by Ciro Santilli, most of them in the format of Stack Overflow answers.
Ciro posts update about new articles on his Twitter accounts.
Some random generally less technical in-tree essays will be present at: Section "Essays by Ciro Santilli".
- Trended on Hacker News:
- CIA 2010 covert communication websites on 2023-06-11. 190 points, a mild success.
- x86 Bare Metal Examples on 2019-03-19. 513 points. The third time something related to that repo trends. Hacker news people really like that repo!
- again 2020-06-27 (archive). 200 points, repository traffic jumped from 25 daily unique visitors to 4.6k unique visitors on the day
- How to run a program without an operating system? on 2018-11-26 (archive). 394 points. Covers x86 and ARM
- ELF Hello World Tutorial on 2017-05-17 (archive). 334 points.
- x86 Paging Tutorial on 2017-03-02. Number 1 Google search result for "x86 Paging" in 2017-08. 142 points.
- x86 assembly
- What does "multicore" assembly language look like?
- What is the function of the push / pop instructions used on registers in x86 assembly? Going down to memory spills, register allocation and graph coloring.
- Linux kernel
- What do the flags in /proc/cpuinfo mean?
- How does kernel get an executable binary file running under linux?
- How to debug the Linux kernel with GDB and QEMU?
- Can the sys_execve() system call in the Linux kernel receive both absolute or relative paths?
- What is the difference between the kernel space and the user space?
- Is there any API for determining the physical address from virtual address in Linux?
- Why do people write the
#!/usr/bin/envpython shebang on the first line of a Python script? - How to solve "Kernel Panic - not syncing: VFS: Unable to mount root fs on unknown-block(0,0)"?
- Single program Linux distro
- QEMU
- gcc and Binutils:
- How do linkers and address relocation works?
- What is incremental linking or partial linking?
- GOLD (
-fuse-ld=gold) linker vs the traditional GNU ld and LLVM ldd - What is the -fPIE option for position-independent executables in GCC and ld? Concrete examples by running program through GDB twice, and an assembly hello world with absolute vs PC relative load.
- How many GCC optimization levels are there?
- Why does GCC create a shared object instead of an executable binary according to file?
- C/C++: almost all of those fall into "disassemble all the things" category. Ciro also does "standards dissection" and "a new version of the standard is out" answers, but those are boring:
- What does "static" mean in a C program?
- In C++ source, what is the effect of
extern "C"? - Char array vs Char Pointer in C
- How to compile glibc from source and use it?
- When should
static_cast,dynamic_cast,const_castandreinterpret_castbe used? - What exactly is
std::atomicin C++?. This answer was originally more appropriately entitled "Let's disassemble some stuff", and got three downvotes, so Ciro changed it to a more professional title, and it started getting upvotes. People judge books by their covers. notmain.o 0000000000000000 0000000000000017 W MyTemplate<int>::f(int) main.o 0000000000000000 0000000000000017 W MyTemplate<int>::f(int)Code 1.. From: What is explicit template instantiation in C++ and when to use it?nmoutputs showing that objects are redefined multiple times across files if you don't use template instantiation properly
- IEEE 754
- What is difference between quiet NaN and signaling NaN?
- In Java, what does NaN mean?
Without subnormals: +---+---+-------+---------------+-------------------------------+ exponent | ? | 0 | 1 | 2 | 3 | +---+---+-------+---------------+-------------------------------+ | | | | | | v v v v v v ----------------------------------------------------------------- floats * **** * * * * * * * * * * * * ----------------------------------------------------------------- ^ ^ ^ ^ ^ ^ | | | | | | 0 | 2^-126 2^-125 2^-124 2^-123 | 2^-127 With subnormals: +-------+-------+---------------+-------------------------------+ exponent | 0 | 1 | 2 | 3 | +-------+-------+---------------+-------------------------------+ | | | | | v v v v v ----------------------------------------------------------------- floats * * * * * * * * * * * * * * * * * ----------------------------------------------------------------- ^ ^ ^ ^ ^ ^ | | | | | | 0 | 2^-126 2^-125 2^-124 2^-123 | 2^-127Code 2.Visualization of subnormal floating point numbers vs what IEEE 754 would look like without them. From: What is a subnormal floating point number?
- Computer science
- Algorithms
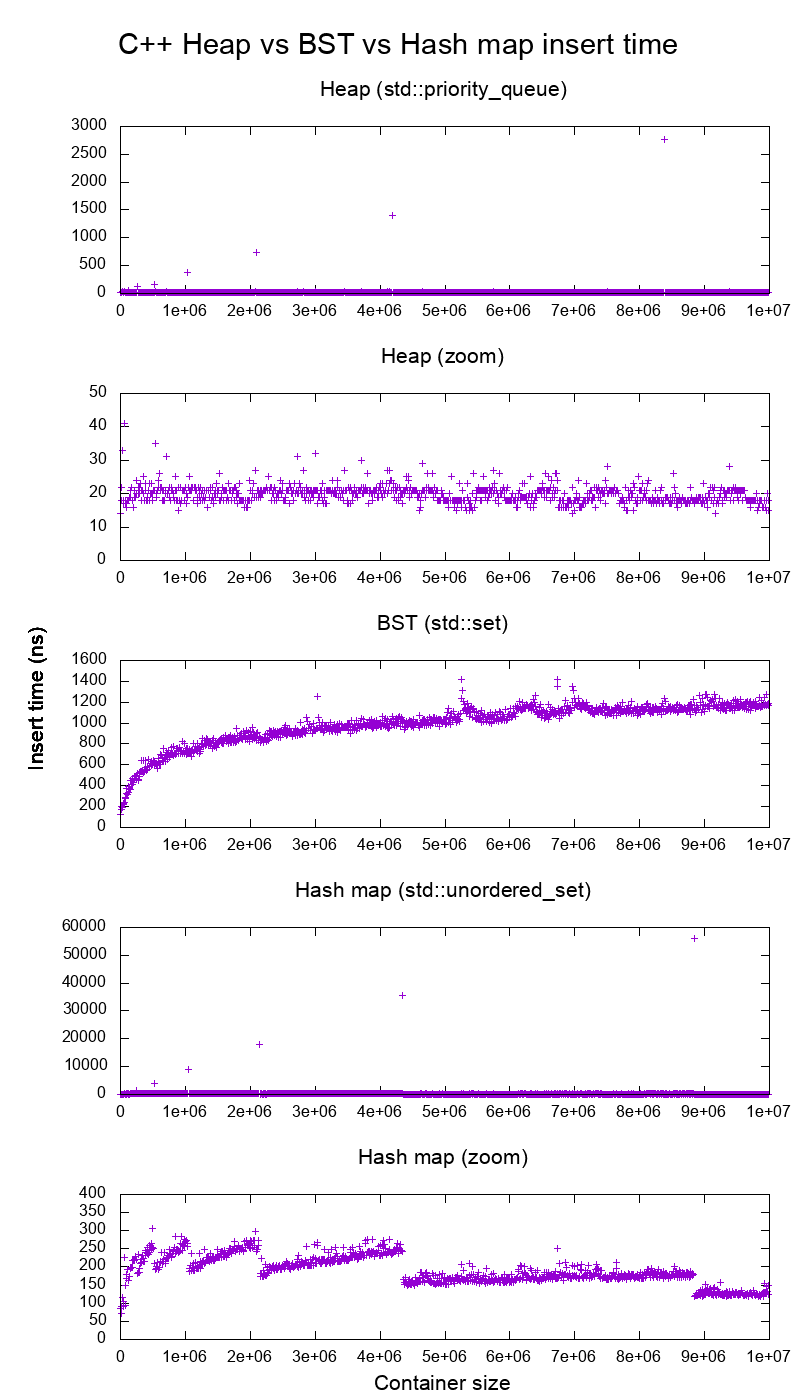
Figure 5. Average insertion time into heaps, binary search tree and hash maps of the C++ standard library. Source. From: Heap vs Binary Search Tree (BST)
- Is it necessary for NP problems to be decision problems?
- Polynomial time and exponential time. Answered focusing on the definition of "exponential time".
- What is the smallest Turing machine where it is unknown if it halts or not?. Answer focusing on "blank tape" initial condition only. Large parts of it are summarizing the Busy Beaver Challenge, but some additions were made.
- Algorithms
- Git
| 0 | 4 | 8 | C | |-------------|--------------|-------------|----------------| 0 | DIRC | Version | File count | ctime ...| 0 | ... | mtime | device | 2 | inode | mode | UID | GID | 2 | File size | Entry SHA-1 ...| 4 | ... | Flags | Index SHA-1 ...| 4 | ... |Code 3.ASCII art depicting the binary file format of the Git index file. From: What does the git index contain EXACTLY?tree {tree_sha} {parents} author {author_name} <{author_email}> {author_date_seconds} {author_date_timezone} committer {committer_name} <{committer_email}> {committer_date_seconds} {committer_date_timezone} {commit message}Code 4.Description of the Git commit object binary data structure. From: What is the file format of a git commit object data structure?- How do I clone a subdirectory only of a Git repository?
- Python
- Web technology
- OpenGL
Figure 7. OpenGL rendering output dumped to a GIF file. Source. From: How to use GLUT/OpenGL to render to a file?- What are shaders in OpenGL?
- Why do we use 4x4 matrices to transform things in 3D?
Figure 10. Sinusoidal circular wave heatmap generated with an OpenGL shader at 60 FPS on SDL. Source.
- Node.js
- Ruby on Rails
- POSIX
- What is POSIX? Huge classified overview of the most important things that POSIX specifies.
- Systems programming
- What do the terms "CPU bound" and "I/O bound" mean?
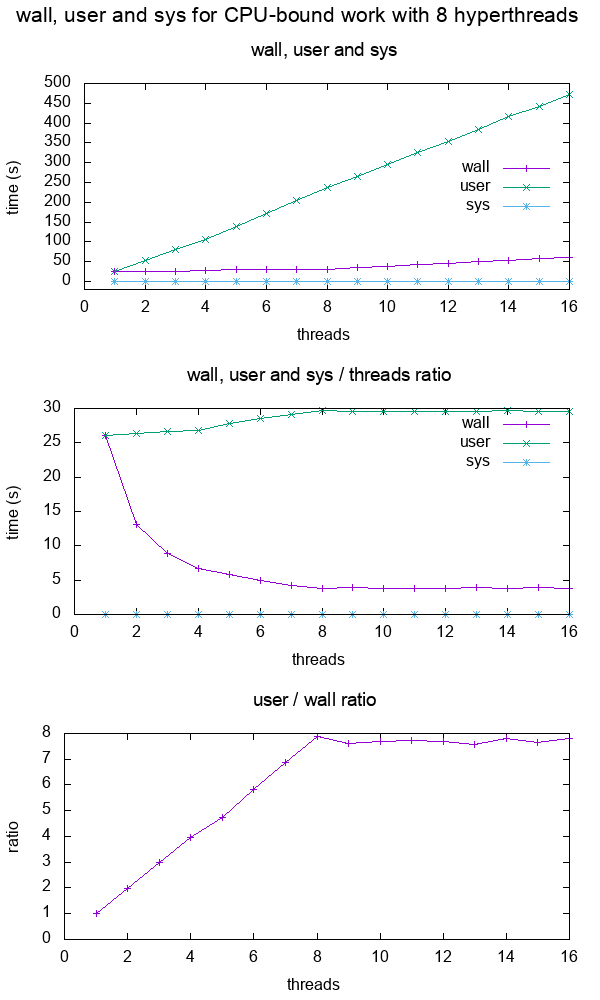
Figure 12. Plot of "real", "user" and "sys" mean times of the output of time for CPU-bound workload with 8 threads. Source. From: What do 'real', 'user' and 'sys' mean in the output of time?+--------+ +------------+ +------+ | device |>---------------->| function 0 |>----->| BAR0 | | | | | +------+ | |>------------+ | | | | | | | +------+ ... ... | | |>----->| BAR1 | | | | | | +------+ | |>--------+ | | | +--------+ | | ... ... ... | | | | | | | | +------+ | | | |>----->| BAR5 | | | +------------+ +------+ | | | | | | +------------+ +------+ | +--->| function 1 |>----->| BAR0 | | | | +------+ | | | | | | +------+ | | |>----->| BAR1 | | | | +------+ | | | | ... ... ... | | | | | | +------+ | | |>----->| BAR5 | | +------------+ +------+ | | | ... | | | +------------+ +------+ +------->| function 7 |>----->| BAR0 | | | +------+ | | | | +------+ | |>----->| BAR1 | | | +------+ | | ... ... ... | | | | +------+ | |>----->| BAR5 | +------------+ +------+Code 5.Logical struture PCIe device, functions and BARs. From: What is the Base Address Register (BAR) in PCIe?
- Electronics
- Raspberry Pi
Figure 13. Raspberry Pi 2 directly connected to a laptop with an Ethernet cable. Image from answer to: How to hook up a Raspberry Pi via Ethernet to a laptop without a router?Figure 14. . Image from answer to: How to hook up a Raspberry Pi via Ethernet to a laptop without a router? Figure 15. . Image from answer to: How to emulate the Raspberry Pi 2 on QEMU? Figure 16. Bare metal LED blinker program running on a Raspberry Pi 2. Image from answer to: How to run a C program with no OS on the Raspberry Pi?
- Raspberry Pi
- Computer security
- Media
Video 2. Canon in D in C. Source.The original question was deleted, lol...: How to programmatically synthesize music?- How to resize a picture using ffmpeg's sws_scale()?
- Is there any decent speech recognition software for Linux? ran a few examples manually on
vosk-apiand compared to ground truth.
- Eclipse
- Computer hardware
- Scientific visualization software
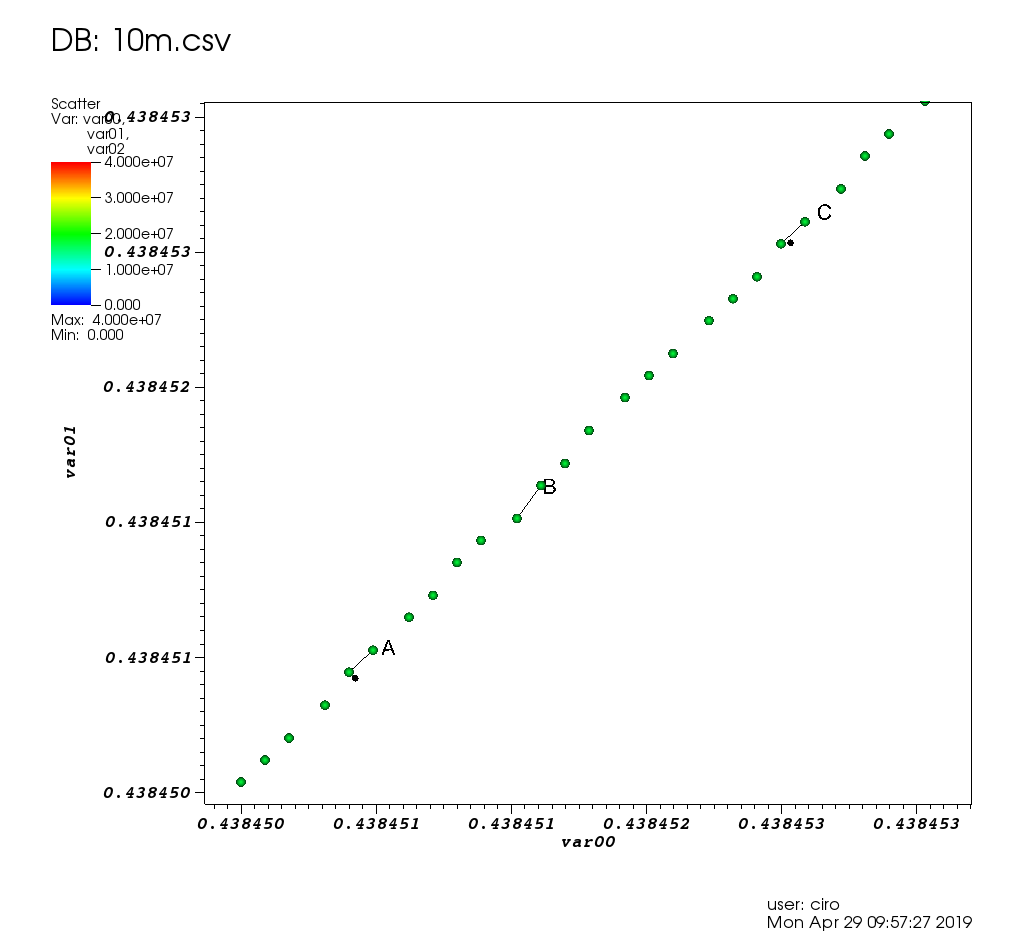
Figure 17. VisIt zoom in 10 million straight line plot with some manually marked points. Source. From: Section "Survey of open source interactive plotting software with a 10 million point scatter plot benchmark by Ciro Santilli"
- Numerical analysis
- Computational physics
- Register transfer level languages like Verilog and VHDL
- Verilog:
Figure 19. . See also: Section "Verilator interactive example"
- Verilog:
- Android
Video 4. Android screen showing live on an Ubuntu laptop through ADB. Source. From: How to see the Android screen live on an Ubuntu desktop through ADB?
- Debugging
- Program optimization
- What is tail call optimization?
Figure 21. . Source. The answer compares gprof, valgrind callgrind, perf and gperftools on a single simple executable.
- Data
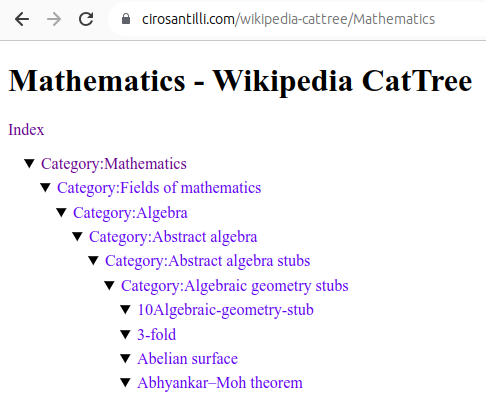
Figure 22. Mathematics dump of Wikipedia CatTree. Source. In this project, Ciro Santilli explored extracting the category and article tree out of the Wikipedia dumps.
- Mathematics
Figure 23. Diagram of the fundamental theorem on homomorphisms by Ciro Santilli (2020)Shows the relationship between group homomorphisms and normal subgroups.- Section "Formalization of mathematics": some early thoughts that could be expanded. Ciro almost had a stroke when he understood this stuff in his teens.
Figure 24. Simple example of the Discrete Fourier transform. Source. That was missing from Wikipedia page: en.wikipedia.org/wiki/Discrete_Fourier_transform!
- Network programming
- Physics
- What is the difference between plutonium and uranium?
Figure 25. Spacetime diagram illustrating how faster-than-light travel implies time travel. From: Does faster than light travel imply travelling back in time?
- Biology
Figure 26. Top view of an open Oxford Nanopore MinION. Source. From: Section "How to use an Oxford Nanopore MinION to extract DNA from river water and determine which bacteria live in it"Figure 27. Mass fractions in a minimal growth medium vs an amino acid cut in a simulation of the E. Coli Whole Cell Model by Covert Lab. Source. From: Section "E. Coli Whole Cell Model by Covert Lab"
- Quantum computing
- Section "Quantum computing is just matrix multiplication"
Figure 28. Visualization of the continuous deformation of states as we walk around the Bloch sphere represented as photon polarization arrows. From: Understanding the Bloch sphere.
- Bitcoin
- GIMP
Figure 29. GIMP screenshot part of how to combine two images side-by-side in GIMP?
- Home DIY
Figure 30. Total_Blackout_Cassette_Roller_Blind_With_Curtains.Source. From: Section "How to blackout your window without drilling"
- China
Electronic design automation Updated 2025-07-16
A set of software programs that compile high level register transfer level languages such as Verilog into something that a fab can actually produce. One is reminded of a compiler toolchain but on a lower level.
The most important steps of that include:
- logic synthesis: mapping the Verilog to a standard cell library
- place and route: mapping the synthesis output into the 2D surface of the chip
Fabless manufacturing Updated 2025-07-16
But once designs started getting very complicated, it started to make sense to separate concerns between designers and fabs.
What this means is that design companies would primarily write register transfer level, then use electronic design automation tools to get a final manufacturable chip, and then send that to the fab.
The term "Fabless" could in theory refer to other areas of industry besides the semiconductor industry, but it is mostly used in that context.
High level quantum synthesis Updated 2025-07-16
This is a term "invented" by Ciro Santilli to refer to quantum compilers that are able to convert non-specifically-quantum (functional, since there is no state in quantum software) programs into quantum circuit.
The term is made by adding "quantum" to the more "classical" concept of "high-level synthesis", which refers to software that converts an imperative program into register transfer level hardware, typicially for FPGA applications.
How computers work? Updated 2025-07-16
A computer is a highly layered system, and so you have to decide which layers you are the most interested in studying.
Although the layer are somewhat independent, they also sometimes interact, and when that happens it usually hurts your brain. E.g., if compilers were perfect, no one optimizing software would have to know anything about microarchitecture. But if you want to go hardcore enough, you might have to learn some lower layer.
It must also be said that like in any industry, certain layers are hidden in commercial secrecy mysteries making it harder to actually learn them. In computing, the lower level you go, the more closed source things tend to become.
But as you climb down into the abyss of low level hardcoreness, don't forget that making usefulness is more important than being hardcore: Figure 1. "xkcd 378: Real Programmers".
First, the most important thing you should know about this subject: cirosantilli.com/linux-kernel-module-cheat/should-you-waste-your-life-with-systems-programming
Here's a summary from low-level to high-level:
- semiconductor physical implementation this level is of course the most closed, but it is fun to try and peek into it from any openings given by commercials and academia:
- photolithography, and notably photomask design
- register transfer level
- interactive Verilator fun: Is it possible to do interactive user input and output simulation in VHDL or Verilog?
- more importantly, and much harder/maybe impossible with open source, would be to try and set up a open source standard cell library and supporting software to obtain power, performance and area estimates
- Are there good open source standard cell libraries to learn IC synthesis with EDA tools? on Quora
- the most open source ones are some initiatives targeting FPGAs, e.g. symbiflow.github.io/, www.clifford.at/icestorm/
- qflow is an initiative targeting actual integrated circuits
- microarchitecture: a good way to play with this is to try and run some minimal userland examples on gem5 userland simulation with logging, e.g. see on the Linux Kernel Module Cheat:This should be done at the same time as books/website/courses that explain the microarchitecture basics.
- instruction set architecture: a good approach to learn this is to manually write some userland assembly with assertions as done in the Linux Kernel Module Cheat e.g. at:
- github.com/cirosantilli/linux-kernel-module-cheat/blob/9b6552ab6c66cb14d531eff903c4e78f3561e9ca/userland/arch/x86_64/add.S
- cirosantilli.com/linux-kernel-module-cheat/x86-userland-assembly
- learn a bit about calling conventions, e.g. by calling C standard library functions from assembly:
- you can also try and understand what some simple C programs compile to. Things can get a bit hard though when
-O3is used. Some cute examples:
- executable file format, notably executable and Linkable Format. Particularly important is to understand the basics of:
- address relocation: How do linkers and address relocation work?
- position independent code: What is the -fPIE option for position-independent executables in GCC and ld?
- how to observe which symbols are present in object files, e.g.:
- how C++ uses name mangling What is the effect of extern "C" in C++?
- how C++ template instantiation can help reduce link time and size: Explicit template instantiation - when is it used?
- operating system. There are two ways to approach this:
- learn about the Linux kernel Linux kernel. A good starting point is to learn about its main interfaces. This is well shown at Linux Kernel Module Cheat:
- system calls
- write some system calls in
- pure assembly:
- C GCC inline assembly:
- write some system calls in
- learn about kernel modules and their interfaces. Notably, learn about to demystify special files such
/dev/randomand so on: - learn how to do a minimal Linux kernel disk image/boot to userland hello world: What is the smallest possible Linux implementation?
- learn how to GDB Step debug the Linux kernel itself. Once you know this, you will feel that "given enough patience, I could understand anything that I wanted about the kernel", and you can then proceed to not learn almost anything about it and carry on with your life
- system calls
- write your own (mini-) OS, or study a minimal educational OS, e.g. as in:
- learn about the Linux kernel Linux kernel. A good starting point is to learn about its main interfaces. This is well shown at Linux Kernel Module Cheat:
- programming language
Logic synthesis Updated 2025-07-16
Step of electronic design automation that maps the register transfer level input (e.g. Verilog) to a standard cell library.
Programmer's model of quantum computers Updated 2025-07-16
This is a quick tutorial on how a quantum computer programmer thinks about how a quantum computer works. If you know:a concrete and precise hello world operation can be understood in 30 minutes.
- what a complex number is
- how to do matrix multiplication
- what is a probability
Although there are several types of quantum computer under development, there exists a single high level model that represents what most of those computers can do, and we are going to explain that model here. This model is the is the digital quantum computer model, which uses a quantum circuit, that is made up of many quantum gates.
Beyond that basic model, programmers only may have to consider the imperfections of their hardware, but the starting point will almost always be this basic model, and tooling that automates mapping the high level model to real hardware considering those imperfections (i.e. quantum compilers) is already getting better and better.
The way quantum programmers think about a quantum computer in order to program can be described as follows:
- the input of a N qubit quantum computer is a vector of dimension N containing classic bits 0 and 1
- the quantum program, also known as circuit, is a unitary matrix of complex numbers that operates on the input to generate the output
- the output of a N qubit computer is also a vector of dimension N containing classic bits 0 and 1
Each time you do this, you are literally conducting a physical experiment of the specific physical implementation of the computer:and each run as the above can is simply called "an experiment" or "a measurement".
- setup your physical system to represent the classical 0/1 inputs
- let the state evolve for long enough
- measure the classical output back out
The output comes out "instantly" in the sense that it is physically impossible to observe any intermediate state of the system, i.e. there are no clocks like in classical computers, further discussion at: quantum circuits vs classical circuits. Setting up, running the experiment and taking the does take some time however, and this is important because you have to run the same experiment multiple times because results are probabilistic as mentioned below.
But the each output is not equally likely either, otherwise the computer would be useless except as random number generator!
This is because the probabilities of each output for a given input depends on the program (unitary matrix) it went through.
Therefore, what we have to do is to design the quantum circuit in a way that the right or better answers will come out more likely than the bad answers.
We then calculate the error bound for our circuit based on its design, and then determine how many times we have to run the experiment to reach the desired accuracy.
The probability of each output of a quantum computer is derived from the input and the circuit as follows.
First we take the classic input vector of dimension N of 0's and 1's and convert it to a "quantum state vector" of dimension :
We are after all going to multiply it by the program matrix, as you would expect, and that has dimension !
Note that this initial transformation also transforms the discrete zeroes and ones into complex numbers.
For example, in a 3 qubit computer, the quantum state vector has dimension and the following shows all 8 possible conversions from the classic input to the quantum state vector:
000 -> 1000 0000 == (1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
001 -> 0100 0000 == (0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
010 -> 0010 0000 == (0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0)
011 -> 0001 0000 == (0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0)
100 -> 0000 1000 == (0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0)
101 -> 0000 0100 == (0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0)
110 -> 0000 0010 == (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0)
111 -> 0000 0001 == (0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0)This can be intuitively interpreted as:
- Therefore, the probability of all three 0's is 1.0, and all other possible combinations have 0 probability.
- if the classic input is
001, then we are certain that bit one and two are 0, and bit three is 1. The probability of that is 1.0, and all others are zero. - and so on
Now that we finally have our quantum state vector, we just multiply it by the unitary matrix of the quantum circuit, and obtain the dimensional output quantum state vector :
And at long last, the probability of each classical outcome of the measurement is proportional to the square of the length of each entry in the quantum vector, analogously to what is done in the Schrödinger equation.
Then, the probability of each possible outcomes would be the length of each component squared:i.e. 75% for the first, and 25% for the third outcomes, where just like for the input:
Keep in mind that the quantum state vector can also contain complex numbers because we are doing quantum mechanics, but we just take their magnitude in that case, e.g. the following quantum state would lead to the same probabilities as the previous one:
This interpretation of the quantum state vector clarifies a few things:
- the input quantum state is just a simple state where we are certain of the value of each classic input bit
- This is true for the input matrix, and unitary matrices have the probability of maintaining that property after multiplication.Unitary matrices are a bit analogous to self-adjoint operators in general quantum mechanics (self-adjoint in finite dimensions implies is stronger)This also allows us to understand intuitively why quantum computers may be capable of accelerating certain algorithms exponentially: that is because the quantum computer is able to quickly do an unitary matrix multiplication of a humongous sized matrix.If we are able to encode our algorithm in that matrix multiplication, considering the probabilistic interpretation of the output, then we stand a chance of getting that speedup.
As we could see, this model is was simple to understand, being only marginally more complex than that of a classical computer, see also: quantumcomputing.stackexchange.com/questions/6639/is-my-background-sufficient-to-start-quantum-computing/14317#14317 The situation of quantum computers today in the 2020's is somewhat analogous to that of the early days of classical circuits and computers in the 1950's and 1960's, before CPU came along and software ate the world. Even though the exact physics of a classical computer might be hard to understand and vary across different types of integrated circuits, those early hardware pioneers (and to this day modern CPU designers), can usefully view circuits from a higher level point of view, thinking only about concepts such as:as modelled at the register transfer level, and only in a separate compilation step translated into actual chips. This high level understanding of how a classical computer works is what we can call "the programmer's model of a classical computer". So we are now going to describe the quantum analogue of it.
- logic gates like AND, NOR and NOT
- a clock + registers
Bibliography:
- arxiv.org/pdf/1804.03719.pdf Quantum Algorithm Implementations for Beginners by Abhijith et al. 2020
Quantum circuits vs classical circuits Updated 2025-07-16
Just like a classic programmer does not need to understand the intricacies of how transistors are implemented and CMOS semiconductors, the quantum programmer does not understand physical intricacies of the underlying physical implementation.
The main difference to keep in mind is that quantum computers cannot save and observe intermediate quantum state, so programming a quantum computer is basically like programming a combinatorial-like circuit with gates that operate on (qu)bits:
For this reason programming a quantum computer is much like programming a classical combinatorial circuit as you would do with SPICE, verilog-or-vhdl, in which you are basically describing a graph of gates that goes from the input to the output
For this reason, we can use the words "program" and "circuit" interchangeably to refer to a quantum program
Also remember that and there is no no clocks in combinatorial circuits because there are no registers to drive; and so there is no analogue of clock in the quantum system either,
Standard cell library Updated 2025-07-16
Basically what register transfer level compiles to in order to achieve a real chip implementation.
After this is done, the final step is place and route.
They can be designed by third parties besides the semiconductor fabrication plants. E.g. Arm Ltd. markets its Artisan Standard Cell Libraries as mentioned e.g. at: web.archive.org/web/20211007050341/https://developer.arm.com/ip-products/physical-ip/logic This came from a 2004 acquisition: www.eetimes.com/arm-to-acquire-artisan-components-for-913-million/, obviously.
The standard cell library is typically composed of a bunch of versions of somewhat simple gates, e.g.:and so on.
Each of those gates has to be designed by hand as a 3D structure that can be produced in a given fab.
Simulations are then carried out, and the electric properties of those structures are characterized in a standard way as a bunch of tables of numbers that specify things like:Those are then used in power, performance and area estimates.