Theory that gases are made up of a bunch of small billiard balls that don't interact with each other.
This theory attempts to deduce/explain properties of matter such as the equation of state in terms of classical mechanics.
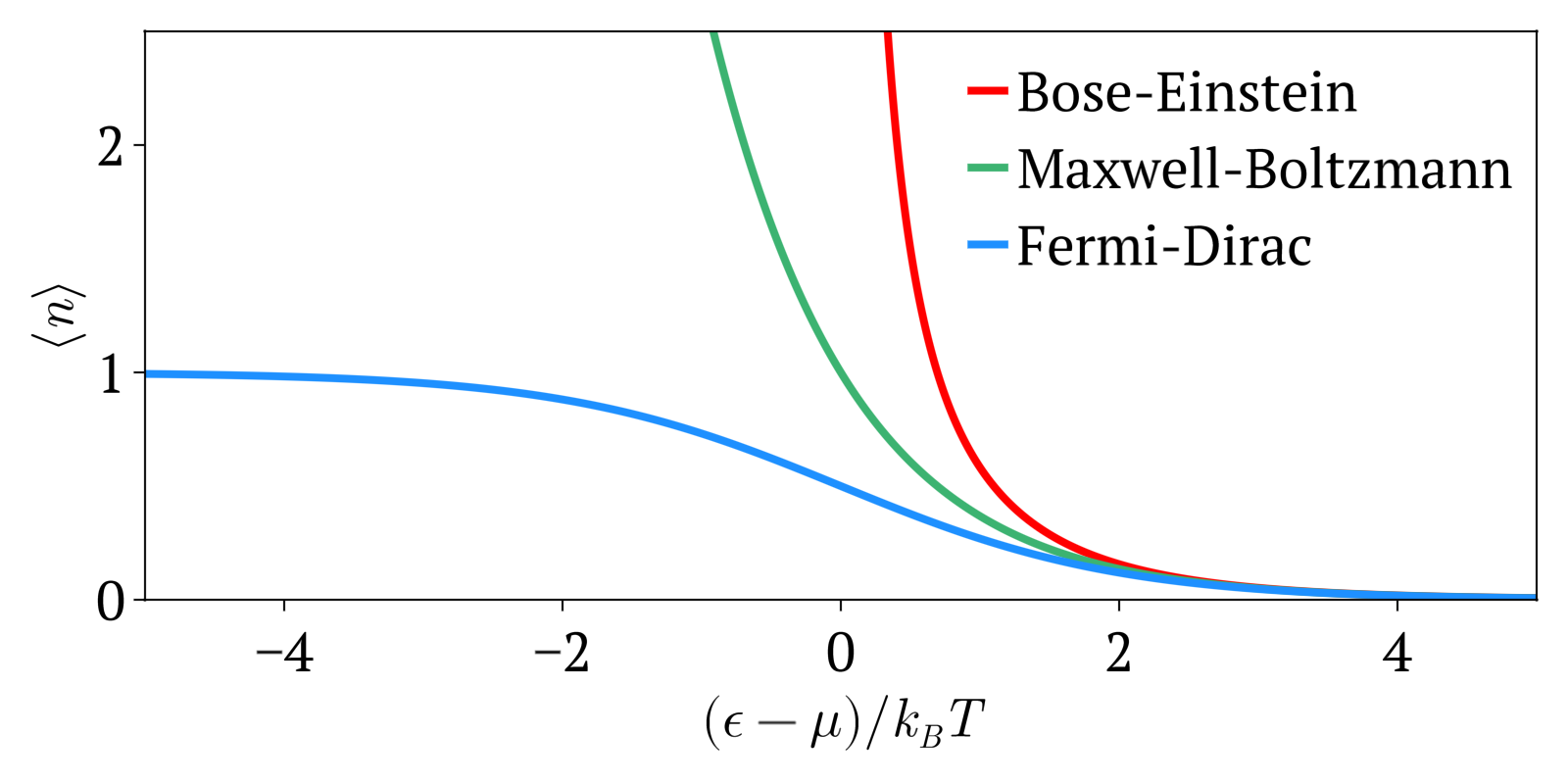
Maxwell-Boltzmann statistics, Bose-Einstein statistics and Fermi-Dirac statistics all describe how energy is distributed in different physical systems at a given temperature.
For example, Maxwell-Boltzmann statistics describes how the speeds of particles are distributed in an ideal gas.
The temperature of a gas is only a statistical average of the total energy of the gas. But at a given temperature, not all particles have the exact same speed as the average: some are higher and others lower than the average.
For a large number of particles however, the fraction of particles that will have a given speed at a given temperature is highly deterministic, and it is this that the distributions determine.
One of the main interest of learning those statistics is determining the probability, and therefore average speed, at which some event that requires a minimum energy to happen happens. For example, for a chemical reaction to happen, both input molecules need a certain speed to overcome the potential barrier of the reaction. Therefore, if we know how many particles have energy above some threshold, then we can estimate the speed of the reaction at a given temperature.
The three distributions can be summarized as:
- Maxwell-Boltzmann statistics: statistics without considering quantum statistics. It is therefore only an approximation. The other two statistics are the more precise quantum versions of Maxwell-Boltzmann and tend to it at high temperatures or low concentration. Therefore this one works well at high temperatures or low concentrations.
- Bose-Einstein statistics: quantum version of Maxwell-Boltzmann statistics for bosons
- Fermi-Dirac statistics: quantum version of Maxwell-Boltzmann statistics for fermions. Sample system: electrons in a metal, which creates the free electron model. Compared to Maxwell-Boltzmann statistics, this explained many important experimental observations such as the specific heat capacity of metals. A very cool and concrete example can be seen at youtu.be/5V8VCFkAd0A?t=1187 from Video "Using a Photomultiplier to Detect single photons by Huygens Optics" where spontaneous field electron emission would follow Fermi-Dirac statistics. In this case, the electrons with enough energy are undesired and a source of noise in the experiment.
Maxwell-Boltzmann vs Bose-Einstein vs Fermi-Dirac statistics
. Source. 
A good conceptual starting point is to like the example that is mentioned at The Harvest of a Century by Siegmund Brandt (2008).
Consider a system with 2 particles and 3 states. Remember that:
- in quantum statistics (Bose-Einstein statistics and Fermi-Dirac statistics), particles are indistinguishable, therefore, we might was well call both of them
A, as opposed toAandBfrom non-quantum statistics - in Bose-Einstein statistics, two particles may occupy the same state. In Fermi-Dirac statistics
Therefore, all the possible way to put those two particles in three states are for:
- Maxwell-Boltzmann distribution: both A and B can go anywhere:
State 1 State 2 State 3 AB AB AB A B B A A B B A A B B A - Bose-Einstein statistics: because A and B are indistinguishable, there is now only 1 possibility for the states where A and B would be in different states.
State 1 State 2 State 3 AA AA AA A A A A A A - Fermi-Dirac statistics: now states with two particles in the same state are not possible anymore:
State 1 State 2 State 3 A A A A A A
Maxwell-Boltzmann distribution for three different temperatures
. Most applications of the Maxwell-Boltzmann distribution confirm the theory, but don't give a very direct proof of its curve.
Here we will try to gather some that do.
Measured particle speeds with a rotation barrel! OMG, pre electromagnetism equipment?
- bingweb.binghamton.edu/~suzuki/GeneralPhysNote_PDF/LN19v7.pdf
- chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Book%3A_Thermodynamics_and_Chemical_Equilibrium_(Ellgen)/04%3A_The_Distribution_of_Gas_Velocities/4.07%3A_Experimental_Test_of_the_Maxwell-Boltzmann_Probability_Density
Is it the same as Zartman Ko experiment? TODO find the relevant papers.
edisciplinas.usp.br/pluginfile.php/48089/course/section/16461/qsp_chapter7-boltzman.pdf mentions
- sedimentation
- reaction rate as it calculates how likely it is for particles to overcome the activation energy
Start by looking at: Maxwell-Boltzmann vs Bose-Einstein vs Fermi-Dirac statistics.
Start by looking at: Maxwell-Boltzmann vs Bose-Einstein vs Fermi-Dirac statistics.
Bibliography:
This is not a truly "fundamental" constant of nature like say the speed of light or the Planck constant.
Rather, it is just a definition of our Kelvin temperature scale, linking average microscopic energy to our macroscopic temperature scale.
The way to think about that link is, at 1 Kelvin, each particle has average energy:per degree of freedom.
For an ideal monatomic gas, say helium, there are 3 degrees of freedom. so each helium atom has average energy:
If we have 2 atoms at 1 K, they will have average energy , and so on.
Another conclusion is that this defines temperature as being proportional to the total energy. E.g. if we had 1 helium atom at 2 K then we would have about energy, 3 K and so on.
This energy is of course just an average: some particles have more, and others less, following the Maxwell-Boltzmann distribution.
chemistry.stackexchange.com/questions/7696/how-do-i-distinguish-between-internal-energy-and-enthalpy/7700#7700 has a good insight:
To summarize, internal energy and enthalpy are used to estimate the thermodynamic potential of the system. There are other such estimates, like the Gibbs free energy G. Which one you choose is determined by the conditions and how easy it is to determine pressure and volume changes.
Adds up chemical energy and kinetic energy.
Wikipedia mentions however that the kinetic energy is often negligible, even for gases.
The sum is of interest when thinking about reactions because chemical reactions can change the number of molecules involved, and therefore the pressure.
To predict if a reaction is spontaneous or not, negative enthalpy is not enough, we must also consider entropy via Gibbs free energy.
Bibliography:
TODO understand more intuitively how that determines if a reaction happens or not.
At least from the formula we see that:
- the more exothermic, the more likely it is to occur
- if the entropy increases, the higher the temperature, the more likely it is to occur
- otherwise, the lower the temperature the more likely it is to occur
A prototypical example of reaction that is exothermic but does not happen at any temperature is combustion.
Lab 7 - Gibbs Free Energy by MJ Billman (2020)
Source. Shows the shift of equilibrium due to temperature change with a color change in a HCl CoCl reaction. Unfortunately there are no conclusions because its student's homework.I think these are the ones where , i.e. enthalpy and entropy push the reaction in different directions. And so we can use temperature to move the Chemical equilibrium back and forward.
Demonstration of a Reversible Reaction by Rugby School Chemistry (2020)
Source. Hydrated copper(ii) sulfate.OK, can someone please just stop the philosophy and give numerical predictions of how entropy helps you predict the future?
The original notion of entropy, and the first one you should study, is the Clausius entropy.
For entropy in chemistry see: entropy of a chemical reaction.
The Biggest Ideas in the Universe | 20. Entropy and Information by Sean Carroll (2020)
Source. In usual Sean Carroll fashion, it glosses over the subject. This one might be worth watching. It mentions 4 possible definitions of entropy: Boltzmann, Gibbs, Shannon (information theory) and John von Neumann (quantum mechanics).TODO why it is optimal: physics.stackexchange.com/questions/149214/why-is-the-carnot-engine-the-most-efficient
Subtle is the Lord by Abraham Pais (1982) chapter 4 "Entropy and Probability" mentions well how Boltzmann first thought that the second law was an actual base physical law of the universe while he was calculating numerical stuff for it, including as late as 1872.
But then he saw an argument by Johann Joseph Loschmidt that given the time reversibility of classical mechanics, and because they were thinking of atoms as classical balls as in the kinetic theory of gases, then there always exist a valid physical state where entropy decreases, by just reversing the direction of time and all particle speeds.
So from this he understood that the second law can only be probabilistic, and not a fundamental law of physics, which he published clearly in 1877.
Considering e.g. Newton's laws of motion, you take a system that is a function of time , e.g. the position of many point particles, and then you reverse the speeds of all particles, then is a solution to that.
I guess you also have to change the sign of the gravitational constant?
TODO can anything interesting and deep be said about "why phase transition happens?" physics.stackexchange.com/questions/29128/what-causes-a-phase-transition on Physics Stack Exchange
The more familiar transitions we are familiar with like liquid water into solid water happen at constant temperature.
However, other types of phase transitions we are less familiar in our daily lives happen across a continuum of such "state variables", notably:
- superfluidity and its related manifestation, superconductivity
- ferromagnetism
Reaches 2 mK[ref]. youtu.be/upw9nkjawdy?t=487 from Video "Building a quantum computer with superconducting qubits by Daniel Sank (2019)" mentions that 15 mK are widely available.
Used for example in some times of quantum computers, notably superconducting quantum computers. As mentioned at: youtu.be/uPw9nkJAwDY?t=487, in that case we need to go so low to reduce thermal noise.
For scales from absolute 0 like Kelvin, is proportional to the total kinetic energy of the material.
The Boltzmann constant tells us how much energy that is, i.e. gives the slope.
Air-tight vs. Vacuum-tight by AlphaPhoenix (2020)
Source. Shows how to debug a leak in an ultra-high vacuum system. Like every other area of engineering, you basically bisect the machine! :-) By Brian Haidet, a PhD at University of California, Santa Barbara. Articles by others on the same topic
There are currently no matching articles.